古典货币模型的识别和参数校准方法

众所周知，在求解DSGE模型之前需要深入分析解的存在性、唯一性和稳定性，即讨论模型结构参数的可识别性。然而，因DSGE模型的结构参数较多，且大部分DSGE模型都是非线性的，目前尚不存在统一的识别分析框架。并且，Nikolay（2010）和Ivana＆Serena（2011）也指出“如果不对结构参数施加识别约束，模型往往是不可识别的，即模型不可求解”。事实上，参数校准是对（部分）稳态结构参数施加了点约束，有助于解决结构参数的不可识别问题。但是，究竟需要对结构参数施加多少个约束以及对哪些结构参数施加约束一直是悬而未决的问题。Ivana＆Serena（2011）指出，若施加的约束个数过多，会导致DSGE模型的过度识别，尽管能够保证结构参数存在唯一的数值解，但并不能保证参数估计具有良好的渐近性质；另外，即使施加的约束个数正确，若对可识别参数施加了约束，则仍然会导致DSGE模型不可识别，使得参数估计值非稳健。为了解决这两方面问题，本书以Gali（2008）古典货币模型为例，讨论如何运用参数校准方法对DSGE模型施加适当的识别约束，实现恰好识别DSGE模型的目的。

（1）识别约束

在第3章，我们已经介绍了Gali（2008）古典货币模型的建模过程以及已对数线性化的DSGE模型（3.32）：

根据第3章的分析，需要识别的结构参数为θ1＝（σ，α，φ，ω，φπ，ρa，ρv）′，其维数为7，计算得到σR，并且根据第3章的定理3.2.1可知结构参数向量θ1是不可识别的。那么，至少需要对θ1中的元素施加一个约束。为此，利用Rothenberg（1971）的秩条件^[2]检验θ1中各个元素的可识别性，考虑到仅仅对模型（3.32）的稳态方程组

根据第3章的分析，需要识别的结构参数为θ1＝（σ，α，φ，ω，φπ，ρa，ρv）′，其维数为7，计算得到σR，并且根据第3章的定理3.2.1可知结构参数向量θ1是不可识别的。那么，至少需要对θ1中的元素施加一个约束。为此，利用Rothenberg（1971）的秩条件^[2]检验θ1中各个元素的可识别性，考虑到仅仅对模型（3.32）的稳态方程组

的参数θc＝（σ，α，φ，ω，φπ）进行参数校准。因此，只需检验θc中各个元素的可识别性。

的参数θc＝（σ，α，φ，ω，φπ）进行参数校准。因此，只需检验θc中各个元素的可识别性。

容易得到，rank［Wσ］＝rank［Wα］＝rank［Wφ］＝rank［Wω］＝7、rank＝6，所以，φπ是可识别参数，不需要对φπ进行参数校准。并且，对参数σ、α、φ以及ω中任意一个参数进行校准，即可得到一个识别约束，从而使得DSGE模型可识别。

（2）参数校准

容易得到，rank［Wσ］＝rank［Wα］＝rank［Wφ］＝rank［Wω］＝7、rank＝6，所以，φπ是可识别参数，不需要对φπ进行参数校准。并且，对参数σ、α、φ以及ω中任意一个参数进行校准，即可得到一个识别约束，从而使得DSGE模型可识别。

（2）参数校准(www.xing528.com)

参数校准并不是严格的统计估计方法，但在数据样本较少或者不可获得的情况下，也不失为一个确定参数的方法。校准的基本思路就是根据模型稳态的变量关系利用实际观测值来确定有关参数（刘斌，2010）。由于模型（3.32）中的各变量不存在趋势项，在利用实际观测数据进行参数校准时，需要首先对实际数据进行剔除趋势项的处理，然后计算退势数据的历史平均值，以此作为分析和计算的基础。具体的分析和计算步骤如下：^[3]由is＝-log Qs及Qs＝β可以看出，若根据国民经济统计中的名义利率取历史平均值作为稳态时的名义利率值，可以得出贴现率β的校准值；②由于1-α反映了劳动收入占产出的比重，可利用收入法统计的GDP计算劳动收入占产出的比重，从而可以得出α的校准值；③由ms＝ps+cs-可知，稳态时实际货币余额的对数是稳态时对数消费（本例中等于对数产出ys）和名义利率的函数。所以，利用实际货币余额样本均值的对数，作为稳态时实际货币余额的对数，并根据所估算的ys、is和Qs计算得到消费与实际货币余额间替代弹性的校准值。

参数校准并不是严格的统计估计方法，但在数据样本较少或者不可获得的情况下，也不失为一个确定参数的方法。校准的基本思路就是根据模型稳态的变量关系利用实际观测值来确定有关参数（刘斌，2010）。由于模型（3.32）中的各变量不存在趋势项，在利用实际观测数据进行参数校准时，需要首先对实际数据进行剔除趋势项的处理，然后计算退势数据的历史平均值，以此作为分析和计算的基础。具体的分析和计算步骤如下：^[3]由is＝-log Qs及Qs＝β可以看出，若根据国民经济统计中的名义利率取历史平均值作为稳态时的名义利率值，可以得出贴现率β的校准值；②由于1-α反映了劳动收入占产出的比重，可利用收入法统计的GDP计算劳动收入占产出的比重，从而可以得出α的校准值；③由ms＝ps+cs-可知，稳态时实际货币余额的对数是稳态时对数消费（本例中等于对数产出ys）和名义利率的函数。所以，利用实际货币余额样本均值的对数，作为稳态时实际货币余额的对数，并根据所估算的ys、is和Qs计算得到消费与实际货币余额间替代弹性的校准值。

至此，根据稳态方程式，利用可观测变量的样本数据得到结构参数β、α及ν的校准值，进而可得到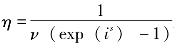及的校准值。

由于校准不可识别参数α是对α实施的识别约束，并且，因rank［Wα］＝7，满足结构参数模型识别的秩条件，即定理3.2.1。所以，只需校准一个稳态参数α，结构模型就是可识别的。但是，由于稳态参数σ、φ和ω仅包含于稳态方程等式ws＝ps+σcs+φns+ωis中，无法借助可观测变量的样本数据直接校准这些参数。

然而，在进行DSGE模型参数校准时，据不完全统计国内相关研究通常并未从参数识别约束的视角讨论施加点识别约束的待校准参数，如胡志鹏（2014）、纪洋等（2015）等。特别是刘斌（2010）指出①“可将结构参数分为两类，一是反映模型稳态特性的参数，二是反映模型动态特性的参数。对于第一类参数，通常采用校准的方法来设定；对于第二类参数，通常采用估计的方法来确定”。而且，对于不能根据模型的稳态方程和可观测变量的样本数据确定的稳态参数，则参考和引用其他类似研究中的估计值直接设定它们的校准值。例如，刘斌（2010）指出^[4]“可根据已有实证研究中货币需求关于利率的长期弹性来得到参数的校准值”。显然，这种参数校准过程将导致两类问题：一类是可能导致结构模型的过度识别，即参数校准过度；另一类是直接引用的参数值未必满足稳态方程，或者，对结构参数施加了错误的识别约束，从而导致其他待估参数的估计偏差。例如，对于本书讨论的稳态方程式（5.8），若直接引用其他研究结果校准参数σ、φ及ω的值，可能会导致参数关系式ω＝χη（ν-σ）无法满足。

因此，从结构识别的视角出发，本书认为校准DSGE模型部分稳态参数的一般步骤如下：首先，检验无识别约束DSGE模型的可识别性，并判断需要施加的识别约束个数；其次，针对对数线性化模型检验参数的可识别性，剔除可识别的结构参数，从而确定需要校准的参数；最后，根据模型的稳态方程和可观测变量的样本数据确定参数的校准值，使得模型的结构参数可识别。例如，对于经济政策分析中常用的An＆Schorfheide（2007）模型，应用Ivana＆Serena（2011）的动态识别方法可以判断无约束DSGE模型是不可识别的，并且通过逐个检验稳态参数的可识别性，最后确定需要校准即施加识别约束的3个稳态参数。

至此，根据稳态方程式，利用可观测变量的样本数据得到结构参数β、α及ν的校准值，进而可得到及的校准值。

由于校准不可识别参数α是对α实施的识别约束，并且，因rank［Wα］＝7，满足结构参数模型识别的秩条件，即定理3.2.1。所以，只需校准一个稳态参数α，结构模型就是可识别的。但是，由于稳态参数σ、φ和ω仅包含于稳态方程等式ws＝ps+σcs+φns+ωis中，无法借助可观测变量的样本数据直接校准这些参数。

然而，在进行DSGE模型参数校准时，据不完全统计国内相关研究通常并未从参数识别约束的视角讨论施加点识别约束的待校准参数，如胡志鹏（2014）、纪洋等（2015）等。特别是刘斌（2010）指出①“可将结构参数分为两类，一是反映模型稳态特性的参数，二是反映模型动态特性的参数。对于第一类参数，通常采用校准的方法来设定；对于第二类参数，通常采用估计的方法来确定”。而且，对于不能根据模型的稳态方程和可观测变量的样本数据确定的稳态参数，则参考和引用其他类似研究中的估计值直接设定它们的校准值。例如，刘斌（2010）指出^[4]“可根据已有实证研究中货币需求关于利率的长期弹性来得到参数的校准值”。显然，这种参数校准过程将导致两类问题：一类是可能导致结构模型的过度识别，即参数校准过度；另一类是直接引用的参数值未必满足稳态方程，或者，对结构参数施加了错误的识别约束，从而导致其他待估参数的估计偏差。例如，对于本书讨论的稳态方程式（5.8），若直接引用其他研究结果校准参数σ、φ及ω的值，可能会导致参数关系式ω＝χη（ν-σ）无法满足。

因此，从结构识别的视角出发，本书认为校准DSGE模型部分稳态参数的一般步骤如下：首先，检验无识别约束DSGE模型的可识别性，并判断需要施加的识别约束个数；其次，针对对数线性化模型检验参数的可识别性，剔除可识别的结构参数，从而确定需要校准的参数；最后，根据模型的稳态方程和可观测变量的样本数据确定参数的校准值，使得模型的结构参数可识别。例如，对于经济政策分析中常用的An＆Schorfheide（2007）模型，应用Ivana＆Serena（2011）的动态识别方法可以判断无约束DSGE模型是不可识别的，并且通过逐个检验稳态参数的可识别性，最后确定需要校准即施加识别约束的3个稳态参数。