DSGE模型及其简化版介绍

动态随机一般均衡（DSGE）模型综合了“动态演化”、“随机冲击”和“一般均衡分析”三种宏观经济学的分析方法，是近30年来在宏观经济研究领域中十分流行的数理经济模型，也是建立结构宏观计量经济学模型的一个崭新领域。特别是在过去的20年里，DSGE模型得到了十分广泛的应用，受到理论与实务界的普遍关注。目前，DSGE模型正在逐渐成为许多研究机构开展宏观经济定量分析的一个基准模型，并且已经成为研究宏观经济波动以及分析财政政策和货币政策效应的重要工具。

国际上对于DSGE模型的研究与应用已经走在了前列，特别是针对DSGE模型的理论研究，例如模型的建立与改进、模型的估计方法研究、模型的识别研究以及脉冲响应分析方法等，许多理论成果为DSGE模型的推广和应用奠定了坚实的基础。

对于DSGE模型的识别研究，始终是DSGE模型理论研究中的一个难点问题。众所周知，DSGE模型体现了理论一致性、模型整体性、微观与宏观经济分析的完美结合、长期与短期分析的有机整合等特点，是一种典型的结构宏观经济学模型。与所有结构模型一样，在求解DSGE模型之前，首先面临的是模型识别的问题。Kydland＆Prescott（1982）最先提出了估计实际经济周期（RBC）模型的参数校准（calibration）方法，这种方法尽管避开了对模型的识别，但是因无法对参数估计值进行有效的统计显著性检验而受到传统计量经济学派的批判，认为其不能被称为求解DSGE模型的估计方法。之后，经济学家们又普遍认为，DSGE模型的脉冲响应函数可以通过一个可估计的VAR（通常是SVAR）模型得到。例如Christiano et al.（2003）建立了一个交错定价模型，并且利用一个10-变量的VAR模型揭示了货币政策冲击的脉冲效应；Woodford＆Rotemberg（1998）通过与VAR模型的脉冲响应函数之间最小距离法估计DSGE模型的参数等。诸如此类研究都旨在说明DSGE模型与VAR（或者SVAR）模型具有相同的简化型——即映射为相同的向量移动平均（VMA）模型。

然而，Ravenna（2007）专门研究了DSGE模型的简化型问题，他指出只有在非常严格的条件下DSGE模型才能够与VAR模型具有相同的脉冲相应函数，并且他给出了相关的充分条件。Ravenna（2007）还进一步提出DSGE模型通常无法映射为一个有限滞后阶的VAR模型，如果所有状态变量都包含在DSGE模型的样本数据中，那么DSGE模型可以映射为一个向量自回归移动平均（VARMA）模型。事实上，在白仲林等（2014）的研究中得到印证，通过对IS-LM-PC模型的推导，发现其可以表示为一个SVARMA模型，进而对化简后的VARMA模型进行识别和估计，得到了准确的脉冲响应函数，从而对各个外生冲击的政策效应进行了有效的分析。另外，白仲林等（2014）对两类DSGE模型分别进行了推导，并得到其动态因子模型（DFM）的表达形式，从而为DSGE模型提供一种新的估计途径。Ivana＆Serena（2011）认为DSGE模型可以改写为状态空间模型（SSM）的形式，并且研究了状态空间模型的识别方法，从而对原DSGE模型结构参数进行识别分析。

可见，关于DSGE模型的简化型选择问题，目前理论界仍没有形成统一的结论。下面主要介绍Ivana＆Serena（2011）将DSGE模型表达为状态空间模型（SSM）的推导过程，以及Ravenna（2007）关于确定DSGE模型简化型的定理。

一般地，一个已对数线性化的DSGE模型，可以表示为一个随机差分方程组：

其中，xt是n×1维的内生状态变量，zt是m×1维的外生状态变量，yt是r×1维的内生变量，εt是m×1维的外生冲击，并且E（εt）＝0，方差—协方差矩阵Var（εt）＝∑。

对差分方程组进行递归求解，则

其中，xt是n×1维的内生状态变量，zt是m×1维的外生状态变量，yt是r×1维的内生变量，εt是m×1维的外生冲击，并且E（εt）＝0，方差—协方差矩阵Var（εt）＝∑。

对差分方程组进行递归求解，则

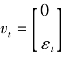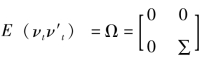其中，并且，＝0（t≠τ）。显然，方程（5.2）是状态方程，而方程（5.3）是测量方程。

Ivana＆Serena（2011）指出，若将DSGE模型中原始的待估参数记为θ，那么方程（5.2）和（5.3）可以表示为状态空间模型：

其中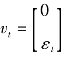，并且，＝0（t≠τ）。显然，方程（5.2）是状态方程，而方程（5.3）是测量方程。

Ivana＆Serena（2011）指出，若将DSGE模型中原始的待估参数记为θ，那么方程（5.2）和（5.3）可以表示为状态空间模型：(www.xing528.com)

Ivana＆Serena（2011）指定式（5.4）为DSGE模型的简化型模型，并识别DSGE模型。

将式（5.2）和（5.3）改写为：

Ivana＆Serena（2011）指定式（5.4）为DSGE模型的简化型模型，并识别DSGE模型。

将式（5.2）和（5.3）改写为：

为了将内生变量yt表示为VAR过程，考虑在稳态时状态变量xt和zt是不变的，那么方程组（5.5）又可以改写为：

为了将内生变量yt表示为VAR过程，考虑在稳态时状态变量xt和zt是不变的，那么方程组（5.5）又可以改写为：

显然，可以利用第3章的对SVAR模型的识别方法通过施加合理的约束分解出结构冲击，从而进行脉冲响应分析。需要注意的是，Yt可以表示为VAR过程的条件为是可观测的，可观测变量的个数n+r恰好等于外生冲击的个数m，并且矩阵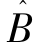是可逆的。于是，如果DSGE模型可以满足上述条件，那么此时DSGE模型与VAR模型具有相同的脉冲相应函数，而一般情况下，在上述条件不满足时，Ravenna（2007）也做出了详细的分析和推导，并给出了如下定理。

命题5.1.1：设

显然，可以利用第3章的对SVAR模型的识别方法通过施加合理的约束分解出结构冲击，从而进行脉冲响应分析。需要注意的是，Yt可以表示为VAR过程的条件为是可观测的，可观测变量的个数n+r恰好等于外生冲击的个数m，并且矩阵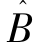是可逆的。于是，如果DSGE模型可以满足上述条件，那么此时DSGE模型与VAR模型具有相同的脉冲相应函数，而一般情况下，在上述条件不满足时，Ravenna（2007）也做出了详细的分析和推导，并给出了如下定理。

命题5.1.1：设

假设xt是不可观测的，可观测变量是r×1维的且r≤r1，并且，外生冲击的个数m＝r，则可观测内生变量yt是一个VARMA（mn+p，mn）过程，其中xt是n×1维的内生状态变量，zt是m×1维的外生状态变量，是r1×1维的内生变量，εt是m×1维的外生冲击，∑为对角阵，Z（L）是关于滞后算子L的矩阵多项式，zt是一个平稳的VAR（p）过程。

假设xt是不可观测的，可观测变量是r×1维的且r≤r1，并且，外生冲击的个数m＝r，则可观测内生变量yt是一个VARMA（mn+p，mn）过程，其中xt是n×1维的内生状态变量，zt是m×1维的外生状态变量，是r1×1维的内生变量，εt是m×1维的外生冲击，∑为对角阵，Z（L）是关于滞后算子L的矩阵多项式，zt是一个平稳的VAR（p）过程。