两类结构参数模型的识别性问题探讨

本节以联立方程组模型（SEM）和结构向量自回归（SVAR）模型的识别为例，说明一般性的定理3.2.1是对经典研究的归纳和推广。

（1）线性联立方程组模型（LSEM）可识别的秩条件

设yt和ut分别为G维随机变量向量，xt为K维非随机外生变量向量，B和∑为G阶非奇异矩阵，Γ为G×K阶矩阵，对于由G个线性方程组成的标准化联立方程组模型^[1]

则对应的简化型为

则对应的简化型为

其中，Π为G×K的矩阵，εt～i.i.d.N（0，Ω），Ω＝B-1∑B′-1。

为了便于表示，本章记结构模型（3.10）的参数向量θ＝（vec（B）′，vec（Γ）′，vec（∑）′）′的集合为Θ，它是空间R（2G+K）G的开子集，并且记简化型模型（3.11）的参数向量λ＝（vec（Π）′，vec（Ω）′）′。

于是，对于已知的Π和Ω，考察方程组

其中，Π为G×K的矩阵，εt～i.i.d.N（0，Ω），Ω＝B-1∑B′-1。

为了便于表示，本章记结构模型（3.10）的参数向量θ＝（vec（B）′，vec（Γ）′，vec（∑）′）′的集合为Θ，它是空间R（2G+K）G的开子集，并且记简化型模型（3.11）的参数向量λ＝（vec（Π）′，vec（Ω）′）′。

于是，对于已知的Π和Ω，考察方程组

根据定理3.2.1，若满足秩条件rank［W（θ）］＝（2G+K）G，则联立方程模型（3.10）可识别，其中φ（θ）＝（φ1（θ）φ2（θ）…φR（θ））′，即

根据定理3.2.1，若满足秩条件rank［W（θ）］＝（2G+K）G，则联立方程模型（3.10）可识别，其中φ（θ）＝（φ1（θ）φ2（θ）…φR（θ））′，即

是对结构参数θ的R个连续可微的识别约束。

是对结构参数θ的R个连续可微的识别约束。

其中G2阶矩阵Δ使得φσΔ＝2φσ（I⊗BΩ）。

因为

其中G2阶矩阵Δ使得φσΔ＝2φσ（I⊗BΩ）。

因为

显然，在W（θ）′的上述乘积中，第一项是2G2+GK阶的非奇异方阵，所以，W（θ）满足秩条件rank［W（θ）］＝（2G+K）G当且仅当rank［Ψ′］＝G2，其中G2×R阶的矩阵

显然，在W（θ）′的上述乘积中，第一项是2G2+GK阶的非奇异方阵，所以，W（θ）满足秩条件rank［W（θ）］＝（2G+K）G当且仅当rank［Ψ′］＝G2，其中G2×R阶的矩阵

因此，由定理3.2.1可得到如下推论。

推论3.2.1：对于线性联立方程组模型（3.10）及其结构参数θ的R个识别约束（3.12），如果rank［Ψ′］＝G2，则线性联立方程组模型（3.10）可识别。

特别，当对结构参数θ的R个识别约束方程（3.12）是Koopmans et al.（1950）对系数［BΓ］的线性约束

因此，由定理3.2.1可得到如下推论。

推论3.2.1：对于线性联立方程组模型（3.10）及其结构参数θ的R个识别约束（3.12），如果rank［Ψ′］＝G2，则线性联立方程组模型（3.10）可识别。

特别，当对结构参数θ的R个识别约束方程（3.12）是Koopmans et al.（1950）对系数［BΓ］的线性约束

其中行向量Ag是矩阵A＝［BΓ］的第g行，Φg是Rg×（G+K）阶矩阵^[2]且rank（Φg）＝Rg，即对第g个方程施加了Rg个独立的线性约束，显然，，则对联立方程组模型（3.10）所有结构参数的约束是

其中行向量Ag是矩阵A＝［BΓ］的第g行，Φg是Rg×（G+K）阶矩阵^[2]且rank（Φg）＝Rg，即对第g个方程施加了Rg个独立的线性约束，显然，，则对联立方程组模型（3.10）所有结构参数的约束是

并且，因不考虑对∑的约束，所以，φσ＝［0］，

并且，因不考虑对∑的约束，所以，φσ＝［0］，

显然，rank［AΦ′g］≤G，g＝1，…，G。

并且，rank［Ψ′］＝G2当且仅当rank［AΦ′g］＝G，g＝1，…，G。

于是，对于线性联立方程组（3.10）及Koopmans et al.（1950）的单方程系数线性约束，定理3.2.1的秩条件与Koopmans et al.（1950）的秩条件等价。因此，此时定理3.2.1的秩条件是联立方程组模型可识别的充分必要条件。^[3]并且，Koopmans et al.的秩条件定理是推论3.2.1的一种特殊情形。

（2）结构向量自回归（SVAR）模型的识别问题

尽管Sims（1980）提出的向量自回归（VAR）模型能够弥补联立方程组（SEM）模型进行经济预测和政策分析的失灵，但是，因扰动项协方差矩阵的非对角特征，使VAR模型不能量化来自外生独立冲击对经济系统各变量的影响，即VAR模型的扰动项未必是独立的外生冲击，这制约了VAR模型在宏观经济政策分析中的应用。为此，结构向量自回归（SVAR）模型得到了广泛的认同和应用，它能够揭示经济系统的静态结构和动态演化机制。

对于一般的SVAR模型

显然，rank［AΦ′g］≤G，g＝1，…，G。

并且，rank［Ψ′］＝G2当且仅当rank［AΦ′g］＝G，g＝1，…，G。

于是，对于线性联立方程组（3.10）及Koopmans et al.（1950）的单方程系数线性约束，定理3.2.1的秩条件与Koopmans et al.（1950）的秩条件等价。因此，此时定理3.2.1的秩条件是联立方程组模型可识别的充分必要条件。^[3]并且，Koopmans et al.的秩条件定理是推论3.2.1的一种特殊情形。

（2）结构向量自回归（SVAR）模型的识别问题

尽管Sims（1980）提出的向量自回归（VAR）模型能够弥补联立方程组（SEM）模型进行经济预测和政策分析的失灵，但是，因扰动项协方差矩阵的非对角特征，使VAR模型不能量化来自外生独立冲击对经济系统各变量的影响，即VAR模型的扰动项未必是独立的外生冲击，这制约了VAR模型在宏观经济政策分析中的应用。为此，结构向量自回归（SVAR）模型得到了广泛的认同和应用，它能够揭示经济系统的静态结构和动态演化机制。

对于一般的SVAR模型

其中yt是n维内生变量向量，B0为非奇异矩阵，p为滞后阶数，Bi为n×n系数矩阵，n维结构冲击向量ut～i.i.d.N（0，I）。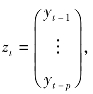

若记n×np的系数矩阵Bl＝［B1…Bp］，np维先决变量向量那么模型有紧凑形式(www.xing528.com)

其中yt是n维内生变量向量，B0为非奇异矩阵，p为滞后阶数，Bi为n×n系数矩阵，n维结构冲击向量ut～i.i.d.N（0，I）。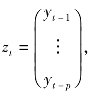

若记n×np的系数矩阵Bl＝［B1…Bp］，np维先决变量向量那么模型有紧凑形式

并且，因假设矩阵B0是非奇异的，则SVAR模型（3.15）的简化型为：

并且，因假设矩阵B0是非奇异的，则SVAR模型（3.15）的简化型为：

于是，对于结构模型（3.15）的识别约束

于是，对于结构模型（3.15）的识别约束

和任意已知的简化型参数λ，考察方程组

和任意已知的简化型参数λ，考察方程组

根据定理3.2.1，若满足秩条件rank［W（θ）］＝n2+n2 p，则SVAR模型（3.15）可识别。

此时

根据定理3.2.1，若满足秩条件rank［W（θ）］＝n2+n2 p，则SVAR模型（3.15）可识别。

此时

从而，由定理3.2.1可得到如下推论。

从而，由定理3.2.1可得到如下推论。

推论3.2.2：对于SVAR模型（3.15）及其结构参数θ的识别约束（3.17），如果＝n（n-1）／2，则SVAR模型（3.15）可识别。

实际上，对于SVAR模型，经典的结构参数识别约束有Hamilton（1994）研究的三角识别约束以及Blanchard＆Quah（1989）和Gali（1992）分别提出的短期识别约束和长期识别约束等。另外，Sims（1986）、King et al.（1991）和Christiano et al.（1996）等文献也分别从特定的经济学观点提出了一些具体的识别约束，其本质依然是对于某个具体的SVAR模型施加一些特殊的识别约束使得能够从简化型参数唯一确定结构参数。但是，与SEM模型的参数识别约束不同，对SVAR模型的参数约束除了对结构系数的线性约束外，还包括非线性约束。

最后，为了分别说明Hamilton（1994）的三角识别约束、Blanchard＆Quah（1989）和Gali（1992）的短期识别约束和长期识别约束均是推论2的特殊情形，本章将SVAR模型结构参数的约束表示为一般形式：

推论3.2.2：对于SVAR模型（3.15）及其结构参数θ的识别约束（3.17），如果＝n（n-1）／2，则SVAR模型（3.15）可识别。

实际上，对于SVAR模型，经典的结构参数识别约束有Hamilton（1994）研究的三角识别约束以及Blanchard＆Quah（1989）和Gali（1992）分别提出的短期识别约束和长期识别约束等。另外，Sims（1986）、King et al.（1991）和Christiano et al.（1996）等文献也分别从特定的经济学观点提出了一些具体的识别约束，其本质依然是对于某个具体的SVAR模型施加一些特殊的识别约束使得能够从简化型参数唯一确定结构参数。但是，与SEM模型的参数识别约束不同，对SVAR模型的参数约束除了对结构系数的线性约束外，还包括非线性约束。

最后，为了分别说明Hamilton（1994）的三角识别约束、Blanchard＆Quah（1989）和Gali（1992）的短期识别约束和长期识别约束均是推论2的特殊情形，本章将SVAR模型结构参数的约束表示为一般形式：

其中Φi是秩为Ri的矩阵，ei表示n阶单位矩阵In的第i列，f（·）是结构参数θ的连续可微函数矩阵。一般情况下，f（·）在点（B0，Bl）处的微分的秩是kn，k是n的倍数。例如，若识别约束直接施加于B0时，则k＝n。若识别约束是Gali（1992）提出的短期加长期约束时，则k＝2n。

①三角识别约束

Hamilton（1994）的三角识别约束是对结构模型（3.15）的参数B0直接施加的线性约束。即，对于结构模型（3.15），存在一个n阶可逆矩阵P使得PB0是下三角矩阵。于是，令f（B0，Bl）＝（PB0）′，Φi是秩为rank［Φi］＝n-i的矩阵，则约束方程组为：

其中Φi是秩为Ri的矩阵，ei表示n阶单位矩阵In的第i列，f（·）是结构参数θ的连续可微函数矩阵。一般情况下，f（·）在点（B0，Bl）处的微分的秩是kn，k是n的倍数。例如，若识别约束直接施加于B0时，则k＝n。若识别约束是Gali（1992）提出的短期加长期约束时，则k＝2n。

①三角识别约束

Hamilton（1994）的三角识别约束是对结构模型（3.15）的参数B0直接施加的线性约束。即，对于结构模型（3.15），存在一个n阶可逆矩阵P使得PB0是下三角矩阵。于是，令f（B0，Bl）＝（PB0）′，Φi是秩为rank［Φi］＝n-i的矩阵，则约束方程组为：

并且，因P是可逆矩阵，则有

并且，因P是可逆矩阵，则有

因此，SVAR模型可识别的三角约束条件正是推论2的秩条件。

②长短期识别约束

因此，SVAR模型可识别的三角约束条件正是推论2的秩条件。

②长短期识别约束

对于SVAR模型3.15，Blanchard＆Quah（1989）和Gali（1992）提出的短期识别与长期识别约束是针对结构参数的非线性约束，即对矩阵B（1）和B（0）元素的零约束，其中B（L）＝是简化型模型VMA（∞）的特征多项式。

于是，如果分别设

对于SVAR模型3.15，Blanchard＆Quah（1989）和Gali（1992）提出的短期识别与长期识别约束是针对结构参数的非线性约束，即对矩阵B（1）和B（0）元素的零约束，其中B（L）＝是简化型模型VMA（∞）的特征多项式。

于是，如果分别设

和适当地选择矩阵Φi，使得＝n（n-1）／2，则识别约束（3.20）即为内生变量关于第i个外生冲击的短（当）期、长期以及长短期的脉冲响应函数的线性约束。

并且，

和适当地选择矩阵Φi，使得＝n（n-1）／2，则识别约束（3.20）即为内生变量关于第i个外生冲击的短（当）期、长期以及长短期的脉冲响应函数的线性约束。

并且，

因此，Blanchard＆Quah（1989）和Gali（1992）关于SVAR模型的识别约束条件正是推论2的秩条件。

类似地，当设定f（B0，Bl）＝［B0 B（0）B（1）］′时，Rubio-Ramirez et al.（2010）对系数零约束和脉冲响应函数零约束的合并约束也是推论2中秩条件的一种特殊形式。

因此，Blanchard＆Quah（1989）和Gali（1992）关于SVAR模型的识别约束条件正是推论2的秩条件。

类似地，当设定f（B0，Bl）＝［B0 B（0）B（1）］′时，Rubio-Ramirez et al.（2010）对系数零约束和脉冲响应函数零约束的合并约束也是推论2中秩条件的一种特殊形式。