识别具有确定参数关系体系结构模型的定理

为了一般性地讨论具有确定参数关系体系结构模型的识别，首先介绍所需要的几个基本假设。①

假设3.2.1：设结构S≡（f，ψ；θ）的结构参数θ为m维向量，并且参数空间Θ是Rm中的开子集。

满足秩条件rank［W（θ）］＝m，则结构S≡（f，ψ；θ）可识别。

证明：定义从参数空间Θ至空间Rn+r的映射F：Θ→Rn+r

假设3.2.2：设结构S的简化型参数λ为n维向量，并且n个函数λi＝（θ）（i＝1，…，n）是连续可微的，即确定的参数关系映射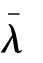（θ）：Θ→Rn是连续可微的。

假设3.2.3：设结构参数θ满足r个约束方程φj（θ）＝0（j＝1，…，r），其中φj（θ）在参数空间Θ上连续可微。

在上述假设下，本章研究发现了如下一般性的识别定理。

①对于结构、结构参数、简化型等相关概念参见第2章2.1。

定理3.2.1：对于满足假设3.2.1—3.2.3的结构S≡（f，ψ；θ），在参数空间Θ上，如果矩阵

满足秩条件rank［W（θ）］＝m，则结构S≡（f，ψ；θ）可识别。

证明：定义从参数空间Θ至空间Rn+r的映射F：Θ→Rn+r

由假设3.2.2—3.2.3可知，F在参数空间Θ上是连续可微的。于是，如果rank［W（θ）］＝m，则m≤n+r，且对于任意的θ0∈Θ，满足。

由假设3.2.2—3.2.3可知，F在参数空间Θ上是连续可微的。于是，如果rank［W（θ）］＝m，则m≤n+r，且对于任意的θ0∈Θ，满足。(www.xing528.com)

根据定理2.2.7，即隐函数定理（Spivak，1965），在θ0的一个邻域内存在唯一的局部逆映射g，满足

显然，SVAR模型（3.6）的简化型为：

由于观测等价的SVAR模型具有

由映射F的定义式，则在θ0的一个邻域内，存在唯一的映射g，满足

由映射F的定义式，则在θ0的一个邻域内，存在唯一的映射g，满足

即必然存在m个单值函数满足

即必然存在m个单值函数满足

此时由简化型参数λ可以唯一确定结构参数θ，即结构S≡（f，ψ；θ）可识别。

显然，只要参数关系体系和对结构参数的约束函数关于结构参数连续可微，便可以应用定理3.2.1的秩条件讨论结构参数模型的可识别性。

当然，一些常见的结构宏观计量经济学模型容易得到反映结构参数和简化型参数关系的参数关系体系，例如，线性联立方程组模型及一般的结构时间序列模型（如SVAR、SVARMA模型等）。但是，也有一些较复杂的结构计量模型其参数关系体系是未知的，例如，Hedonic（Ekeland et al.，2004）模型、DSGE模型及Euler方程模型（Lewbel et al.，2011）等。对于这类结构参数模型的识别问题，将分别在第4章和第5章进行分析和讨论。