相关数学概念：介绍、定义、应用

设Rn≡R×…×R×R＝｛（x1，…，xn），i＝1，…，n｝是n维欧氏空间，Rn的元素被称为点或向量，记为行向量：

设Rn≡R×…×R×R＝｛（x1，…，xn），i＝1，…，n｝是n维欧氏空间，Rn的元素被称为点或向量，记为行向量：

或者列向量：

或者列向量：

并且，对任意给定的向量，xi为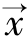中的第i个元素。

（1）Rn的子空间

并且，对任意给定的向量，xi为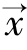中的第i个元素。

（1）Rn的子空间

定义2.2.1：设V是Rn里的非空子集，如果对任意的和任何的（α，β）∈R2都有，则称V是Rn的子空间。

定义2.2.1：设V是Rn里的非空子集，如果对任意的和任何的（α，β）∈R2都有，则称V是Rn的子空间。

显然，对于子空间V的任意一个向量，子空间也包括零元素。特别，存在两个特殊的子空间，Rn本身和零元素组成的子空间。

定义2.2.2：对于任意给定的V∈Rn，设

显然，对于子空间V的任意一个向量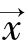，子空间也包括零元素。特别，存在两个特殊的子空间，Rn本身和零元素组成的子空间。

定义2.2.2：对于任意给定的V∈Rn，设

则称V是Rn中所有经过原点的直线构成的子空间。

则称V是Rn中所有经过原点的直线构成的子空间。

定义2.2.3：U和V是Rn的两个子集，并且，则Rn的子集合

定义2.2.3：U和V是Rn的两个子集，并且，则Rn的子集合

被称为U和V的直和。

显然，直和U⊕V具有以下良好的性质。

被称为U和V的直和。

显然，直和U⊕V具有以下良好的性质。

并且，如果U和V是Rn中互补的子空间，则U⊕V＝Rn。例如，在平面上，两个坐标轴是互补的子空间，则

并且，如果U和V是Rn中互补的子空间，则U⊕V＝Rn。例如，在平面上，两个坐标轴是互补的子空间，则

定义2.2.4：设H是Rn的子空间，如果存在，使得，则称H是Rn的超平面。

显然，超平面又称为Rn的最大子空间，也就是说，如果S≠H是Rn的其他任意子空间，若H⊂S，则S＝Rn。并且，在R2里，超平面是经过原点的直线，它是包括原点的特殊平面。

（2）基底

定义2.2.4：设H是Rn的子空间，如果存在，使得，则称H是Rn的超平面。

显然，超平面又称为Rn的最大子空间，也就是说，如果S≠H是Rn的其他任意子空间，若H⊂S，则S＝Rn。并且，在R2里，超平面是经过原点的直线，它是包括原点的特殊平面。

（2）基底

显然，Rn中有很多不同的基底，而最常用的一个特殊基底则是Rn的标准基底。(www.xing528.com)

显然，Rn中有很多不同的基底，而最常用的一个特殊基底则是Rn的标准基底。

定义2.2.8：Rn的标准基底由n个向量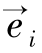的集合组成，i＝1，…，n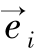，是在第i个位置上取值为1和其他位置上取值为0的向量。

定义2.2.8：Rn的标准基底由n个向量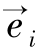的集合组成，i＝1，…，n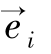，是在第i个位置上取值为1和其他位置上取值为0的向量。

为了界定子空间的标准正交化基底，下面介绍向量的内积和模的概念。

（3）内积和模

为了界定子空间的标准正交化基底，下面介绍向量的内积和模的概念。

（3）内积和模

定义2.2.10：对于任意向量，则称

定义2.2.10：对于任意向量，则称

为向量的内积，并且称

为向量的内积，并且称

为向量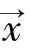的模。

特别，向量的内积和模具有如下的性质。

为向量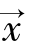的模。

特别，向量的内积和模具有如下的性质。

定理2.2.3：对于任意的向量和常数c∈R，则

定理2.2.3：对于任意的向量和常数c∈R，则

特别地，当＝0时，称向量是正交的。显然，由定义2.2.7可知，Rn的标准基底元素是互相正交的，因此，该基底是正交的。并且，Rn的标准基底元素的模等于1。

定义2.2.11：设E是n维欧式空间Rn的子空间，如果一个映射d：E×E→R满足如下性质：

特别地，当＝0时，称向量是正交的。显然，由定义2.2.7可知，Rn的标准基底元素是互相正交的，因此，该基底是正交的。并且，Rn的标准基底元素的模等于1。

定义2.2.11：设E是n维欧式空间Rn的子空间，如果一个映射d：E×E→R满足如下性质：

则称d为集合E的一个度量，并称组合（E，d）为度量空间。

定义2.2.12：设V是Rn的一个子空间，x0∈Rn，则称Rn的子集合

S＝V+（x0）≡｛y∈Rn｜y＝v+x0，v∈V｝

为Rn的线性流形。

则称d为集合E的一个度量，并称组合（E，d）为度量空间。

定义2.2.12：设V是Rn的一个子空间，x0∈Rn，则称Rn的子集合

S＝V+（x0）≡｛y∈Rn｜y＝v+x0，v∈V｝

为Rn的线性流形。