配送线路的优化设计：简单便捷又经济的解决方案

（一）配送线路优化设计的意义

对配送路线进行设计时，需要考虑很多因素，如现有的道路网络分布，配送客户的地理分布，配送时的本地流量、道路施工，政府对某些线路的管制等。各种因素互相影响，容易造成送货不及时、服务水平下降、配送成本高等问题。配送线路设计就是整合影响配送运输的各因素，适时适当地利用现有的运输工具，结合道路状况，及时、安全、方便、经济地将客户所需的物资准确地送达，提供优良的物流配送服务。在运输线路设计中，需要根据不同客户群的特点和要求，选择不同的线路，最终达到节省时间、缩短运行距离和降低运行费用的目的。

（二）直送式配送线路优化设计

当由一个配送中心向一个特定的客户进行专门送货时，如果客户的需求量接近或大于可用车辆的额定载重量时，需专门派一辆车一次或多次送货，即为直送式配送。在进行直送式配送线路设计时，追求的是最短配送距离，从而节省时间、多装快跑，提高配送效率。因此，直送式配送线路的物流优化，主要是寻找物流网络中的最短线路。

目前公认的最好方法是Dijkstra 算法（迪克斯特拉算法），这种方法是由Dijkstra 于1959年提出来的，也称标号法，如图4-9所示。

假设用dij 表示运输线路中两点i 与j 相邻时的距离，用Lsi 表示从初始点Ps 到点Pi 的最短路线长度。现要求从点Ps 到点Pi 的最短路线，该算法步骤如下。

步骤1：从初始点Ps 出发，逐一给其他点标号。

给点Pi 标上（αi，βi），其中αi 为初始点到点Pi 的最短路长，即αi = Lsi；βi 为点Pi在最短路线上来源点（亦即Pi 是从哪一点来的）的代号；Lsi 的数值标注在点Pi 的旁边的小方框内；至此表示点Pi 已标号。首先给初始点标号（0，0），Lss = 0。

步骤2：找出与点Ps 相邻点中路长最小的一个，若几个点同时达到最小，就都找出来。

设找出的点为r，将（αr，βr）（其中βr =s）和Lsr = Lss + dsr 的值标注给点Pr，表明点Pr 也已标号。

步骤3：从已标号的点出发，找出这些点相邻的所有点。

把每个已标号点（如点Pi ）旁标注的数字[如（αi，βi）和Lsi ]和与之相邻的点（如点Pj ）到这个已标号点（如点Pi ）间的距离dij[边（Pi，Pj）的长度]加起来，从所有和中选出最小的。如这个最小的和是Lsk + dkq ，再找出最小和对应的未标号点，比如q（当几个都为最小时，把它们对应的不同的未标号都找出来），然后给这个点（比如q 点）标号（αq，βq），其中βq = k，Lsq = Lsk + dkq。

步骤4：重复步骤3，直到给点Pt 标上号（αt，βt）和Lst 为止。

步骤5：从点Pt 开始根据各点的标号（αi，βi）反向寻找点Ps 到点Pt 的最短路线所关联的边（Pi，Pj），并将其加粗。

以上得到的由加粗边构成的点Ps 到点Pt 的路径即为点Ps 到点Pt 间的最短路线，其长度为Lst。

例4-1　用DijkStra 算法找出图4-9 中从点P1 到点P8 的最短路线。

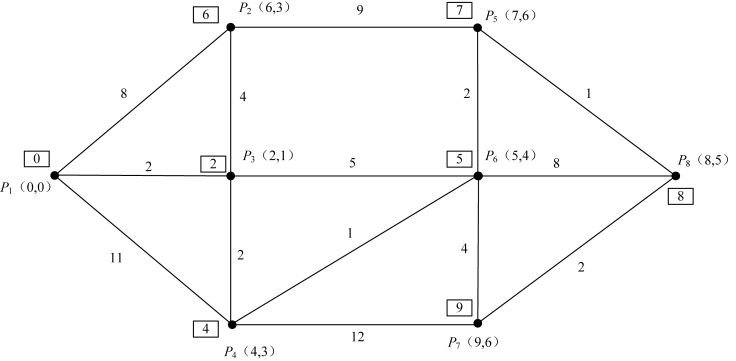
图4-9　DijkStra 算法

（1）从P1 出发，首先给P1 标号（0，0），L11 = 0。

（2）对点 P1，与其相邻的未标号的点有 P2，P3，P4 三点，min（L11 + d12，L11+ d13，L11 + d14）=min（0 + 8，0 + 2，0 + 11）=2，因此，对应最小值的点为P3，给点P3标号（2，1），且L13 = 2。

（3）对已经标号的点P1、P3，与其相邻的未标号的点有 P2，P4，P6 三点，min（L11+ d12，L13 + d32，L13 + d36，L11 + d14，L13 + d34）=min（0 +8，2 +4，2 +5，0 +11，2 +2）=4，因此，对应最小值的点为P4，给点P4 标号（4，3），且L14 = 4。

（4）对已经标号的点P1、P3、P4，与其相邻的未标号的点有P2，P6，P7 三点，min（L11+ d12，L13 + d32，L13 + d36，L14 + d46，L14 + d47）=min（0 +8，2 +4，2 +5，4 +1，4 +12）=5，因此，对应最小值的点为P6，给点P6 标号（5，4），且L16 = 5。

（5）对已经标号的点P1、P3、P4、P6，与其相邻的未标号的点有P2，P5，P7，P8 四点，min（L11 + d12，L13 + d32，L16 + d65，L16 + d68，L16 + d67，L14 + d47）= min（0+8，2+4，5+2，5 +8，5 +4，4 +12）= 6，因此，对应最小值的点为P2，给点P2 标号（6，3），且L12 = 6。

（6）对已经标号的点P1、P3、P4、P6、P2，与其相邻的未标号的点有P5，P7，P8 三点，min（L12 + d25，L16 + d65，L16 + d68，L16 + d67，L14 + d47）=min（6 +9，5 +2，5 +8，5 +4，4 + 12）= 7，因此，对应最小值的点为P5，给点P5 标号（7，6），且L15 = 7。

（7）对已经标号的点P1、P3、P4、P6、P2、P5，与其相邻的未标号的点有P7，P8 三点，min（L15 + d58，L16 + d68，L16 + d67，L14 + d47）=min（7 +1，5 +8，5 +4，4 +12）=8，因此，对应最小值的点为P8，给点P8 标号（8，5），且L18 = 8。

（8）对最后的未标号点P7 来说，min（L18 + d87，L16 + d67，L14 + d47）=min（8 + 2，5 +4，4 + 12）= 9，因此，对应最小值的点为P7，给点P7 标号（9，6），且L17 = 9。

至此，已完成对图中所有点的标号，P1 到各点的最短路线和路长已经求出。由此可见，从点P1 到点P8 的最短路长为8，最短路线为：P1 →P3 →P4 →P6 →P5 →P8。

直送式配送线路适用条件及效果

直送式配送线路适用条件：

①由配送中心向每一位客户开展专门送货。

②该客户的送货量必须满足配送车辆满载。

期望达到的配送效果：

①配送车辆满载运输。

②配送运输路线距离最短。

（三）分送式配送线路优化设计

当由一个配送中心向多个客户进行共同送货，在同一条线路上的所有客户的需求量总和不大于一辆车的额定载重量时，由这一辆车装载所有客户的货物，沿着一条精心设计的最佳路线依次将货物送到各位客户手中，即为分类式配送。这样既保证按时按量将用户需要的货物及时送达，又节约了车辆，节约了行驶里程，节省了费用，缓解了交通压力。分送式配送线路优化可以采用节约里程法。

1.节约里程法的基本思想

如果一个配送中心分别向N 个客户配送货物，在汽车载重能力允许的前提下，每辆汽车在配送路线上经过的客户个数越多，里程节约量越大，配送线路越合理。

2.节约里程法的线路设计原理

设P 点为配送中心所在地，A 和B 为客户所在地，三者相互间的道路距离分别为PA，PB，AB。送货时最直接的想法是利用两辆车分别为A 和B 进行配送，此时车辆的实际运行距离为2PA + 2PB，运输线路如图4 - 10（a）所示。然而，如果改用一辆车巡回配送，则运行的实际距离为PA +PB +AB，如图4 -10（b）所示。当道路状况没有特殊规定时，可节约车辆运行距离为（2PA+2PB）-（PA+PB+AB）=PA+PB-AB。根据三角形两边之和大于第三边的定理，即PA + PB - AB >0，则这个节约量称为节约里程。

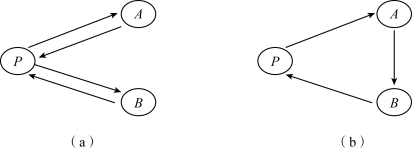
图4-10　分送式配送线路示意

（a）2PA+2PB 模式；（b）PA+PB-AB 模式

节约里程法的基本规定：配送的是同种或相似的货物；各客户的位置及需求量已知；配送中心有足够的运输能力。

除此之外，还应满足以下条件：满足所有用户的要货需求；每辆车不能超载；每车每天总运行时间或行驶里程不能超出规定上限；方案能满足所有用户。

3.节约里程法的求解过程

给数个客户进行配送时，首先计算包括配送中心在内的相互之间的最短距离，然后计算各客户之间的可节约的运行距离，按照节约运行距离的大小顺序连接各配送地点，从而设计出配送路线。(www.xing528.com)

下面举例说明节约里程法的求解过程。

例4-2　某配送中心P 向它旗下的10 家连锁商店a，b，c，d，e，f，g，h，i，j 配送商品，其配送网络如图4-11所示。

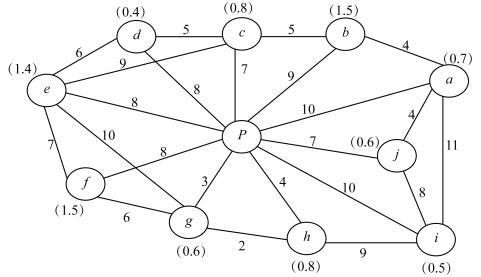
图4-11　配送中心网络示意

图中括号内的数字表示每一家连锁店的需求量qi，单位为吨；线路上的数字表示两节点之间的距离d0j，单位为千米。配送中心现有2 吨和4 吨车辆可供使用，并且每辆车配送距离不得超过30 千米。请为该配送中心制定最优的配送方案。

步骤1：计算网络结点之间的最短距离。

作出最短距离矩阵，从配送网络图中列出配送中心至用户相互间的最短距离矩阵，如图4-12所示。

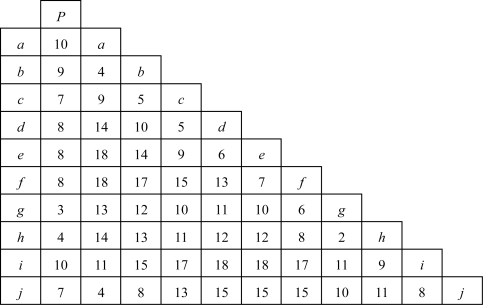
图4-12　最短距离矩阵

步骤2：计算各客户之间可节约的运行距离。

从最短距离矩阵中，计算用户相互间的节约里程，以b—c 的节约行程计算过程为例：P—b 的距离为9，P—c 的距离为7，b—c 的距离为5，则b—c 的节约行程为9 +7 -5 =11。

所有用户（包括配送中心）相互之间的节约里程计算结果如图4-13所示。

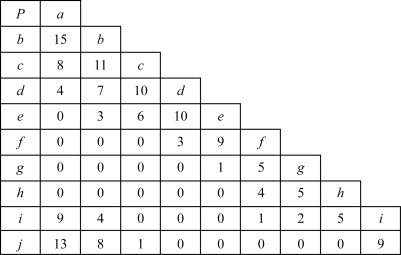
图4-13　节约里程矩阵

步骤3：对节约里程数按大小顺序进行排列，结果如表4-1所示。

表4-1　节约里程排序表

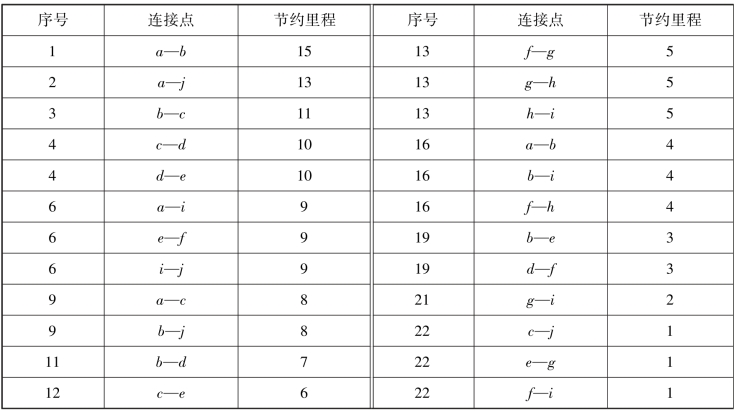
步骤4：组成配送路线图。

初始方案：从配送中心出发，需要设计10 条配送线路，分别向10 家连锁店配送商品；需要10 辆2 吨的配送车辆（每家连锁店的需要量都低于2 吨），总配送距离为148 千米。初始方案配送路线如图4-14所示。

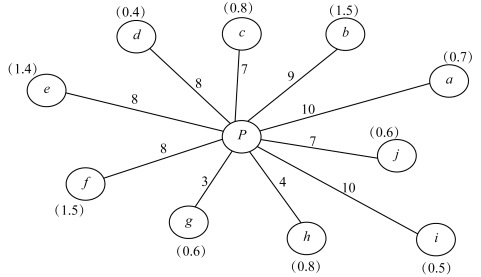
图4-14　初始方案配送路线

第一次修正方案：按节约里程大小顺序，组成配送线路，先将a—b，a—j，b—c 连接起来，形成巡回路线，同时取消P—a，P—b 的路线。规划线路1 装载货物3.6 吨，运行距离27 千米，未超过30 千米。此时，共有7 条线路，运行总距离109 千米，需要2 吨车6辆，4 吨车1 辆。第一次修正方案配送路线如图4-15所示。

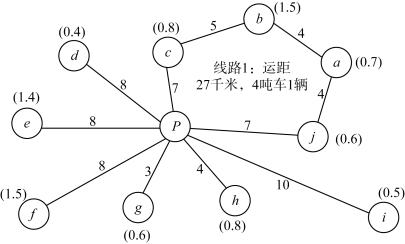
图4-15　第一次修正方案配送路线

第二次修正方案：按节约里程的大小顺序连接c—d 和d—e，这两条线都有可能并到线路1 中，但由于车辆配送距离的限制，不能并入线路1。因此，连接d—e，形成线路2，这样线路2 的载重量为1.8 吨，运行距离为22 千米，未达到各项限制条件。考虑到线路的均衡性和车辆利用率，按节约里程的大小顺序，将a—i，e—f，i—j 并入现有路线，因为连锁店a、j 已并入线路1，受到车辆额定载重和配送距离的限制，线路1 不能增加客户，故不连接a—i，i—j，因此将e—f 并入线路2，这样，新的线路2 运行距离为29 千米，装载量为3.3 吨。继续考虑将其他点连接并入，按照节约里程的大小顺序是a—c，b—j，b—d，c—e，因为这些客户都已经包含在线路1 和线路2 中，因此不进行连接。按照节约里程的大小顺序，继续考虑f—g，将其并入线路2。新的线路2 运行距离为30 千米，装载量为3.9 吨，此时由于车辆最远配送距离的限制，线路2 也不可再增加客户。此时，共有4 条线路，运行总距离85 千米，需要2 吨车2 辆，4 吨车2 辆。第二次修正方案配送路线如图4-16所示。

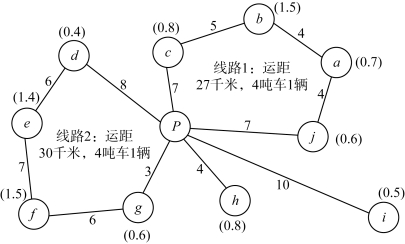
图4-16　第二次修正方案配送路线

第三次修正方案：按节约里程的大小顺序，接下来是g—h 和h—i，由于配送距离的限制，g—h 不能并入线路2，因此连接h—i，形成线路3，其运行距离为23 千米，装载量为1.3 吨。此时，共有3 条线路，运行总距离80 千米，需要2 吨车1 辆，4 吨车2 辆。第三次修正方案配送路线如图4-17所示。

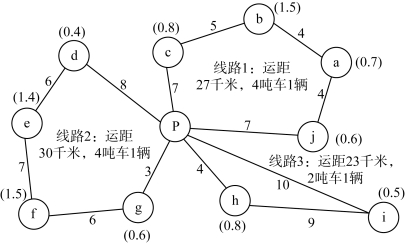
图4-17　第三次修正方案配送路线

综上所述，该配送中心的最优配送方案为：

线路1：P →j →a →b →c →P。

线路2：P →d →e →f →g →P。

线路3：P →h →i →P。

分送式配送线路适用条件及效果

分送式配送线路适用条件：

①由配送中心向多位客户开展拼装送货。

②每位客户的送货量都不能满足配送车辆满载。

配送效果：

①配送车辆满载运输。

②配送运输路线距离最短。

4.节约里程法注意事项

①适用于有稳定客户群的配送中心。

②各配送线路的负荷要尽量均衡。

③实际选择线路时还要考虑道路情况。

④要考虑驾驶员的作息时间及客户要求的交货时间。