决策中的风险性：如何面对多种可能性？

如果决策者能依据过去的有关历史资料或根据多年的实践经验估计出各种情况可能出现的机会，就可采用概率分析进行决策。在决策分析中，如果决策方案中的各项条件都是已知的，但未来发展状况不能确定，每一方案的执行都可能会出现若干种不同的结果，同时可依据有关资料对各种可能出现的结果分别确定其发生的概率，这样的决策就称为“风险性决策”。

（一）概率与概率分析

许多经济要素的未来发展状况是不确定的，可能会出现多种不同的结果，用概率论的术语就是发生多个事件或随机变量。出现某一随机变量的可能性相对于所有事件的集合用比率表现就是该随机变量的概率（probability）。所谓概率分析，就是以概率论原理为基础，针对那些有多种可能结果的不确定因素而采取的一种定量分析方法。

不同随机变量发生概率的大小往往是有区别的。概率分析不仅要充分考虑各种可能事件，而且要用概率来反映各种可能，进而估计特定研究对象未来最有可能达到的水平。

概率分析通常要经过以下三个步骤：

第一步，针对分析对象确定未来可能出现的每一种事件（即随机变量），并为每一事件的发生估计一个概率。概率的估计既可以在会计、统计或其他业务历史数据的基础上进行预测推算，也可以由决策者根据以往经验凭其主观判断加以确定。按前一种方法确定的概率称为客观概率，按后一种方法确定的概率称为主观概率。若以Pi表示第i种事件发生的概率，那么各种事件的概率必须符合以下两条规则：

（1）每种事件的概率在0和1之间，即0＜Pi＜1；

（2）所有可能事件的概率之和必须等于1，即。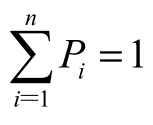

第二步，根据每种事件及其估计的概率，编制概率分析表，计算数学期望值（expected value）。期望值的计算公式如下：

式中：

E为随机变量X的期望值；

Xi为随机变量X的各种可能取值；

Pi为与Xi相对应的概率；

n为随机变量X各种可能取值的数目。

公式中的随机变量Xi会因分析的内容不同而有所不同。如果随机变量是由多个不确定因素决定的，则上式中每一随机变量的相应概率必须按其决定因素的联合概率来确定。数学期望值的实质是一种以随机变量为基础，以相应概率为权数计算的加权平均值。

第三步，根据因素的期望值或在此基础上求得的有关期望值指标进行决策。决策者一般会选择期望值有利的方案，即选择利润期望值最大的方案，或选择成本期望值最小的方案。

这里需要强调的是，对于风险性决策，虽然可以用期望值进行方案的选择，然而不同的决策者最终可能会选择不同的结果，这主要取决于决策者对待风险的态度。根据决策者对待风险的态度，可以将决策者分为三类：风险偏好者、风险中性者和风险回避者。

风险偏好者（risk seeker）是指不管风险多么大，总是对最好的结果感兴趣的决策者。他们愿意承担较大的风险，只要承担这样的风险可以获得较大的收益，他们就会认为承担这样的风险是值得的。

风险中性者（risk neutral）是指关注最有可能结果的决策者。他们更注重用期望值做决策，然而选择期望值最好的方案并不能保证企业的决策是最优的。

风险回避者（risk averse）是指总是关注最坏结果的决策者。他们会尽量避免选择收益较大但风险也较大的方案，而更愿意实施收益较小但风险也较小的方案。

由此可见，对同一方案进行决策分析时，不同的决策者可能会选择不同的结果。

（二）风险性决策分析举例

【例6-14】新亚公司准备在下一年度利用其剩余生产能力生产一种新产品。该公司现有甲、乙两种新产品可供选择，有关两种产品的预计售价及变动成本资料如下：产品甲的销售价格为560元，单位变动成为400元；产品乙的销售价格为500元，单位变动成为320元。甲、乙两种产品的销售量是一随机变量，有关下年销售量预测资料如表6-36所示。

表6-36　销售量概率分布

要求：确定应该生产哪种新产品？

对这种类型的决策，可采用边际贡献分析法。(www.xing528.com)

首先，计算两种产品的单位边际贡献：

根据上述资料计算各方案的边际贡献期望值如下：

从上面的计算可以看出：虽然产品乙的单位边际贡献大于产品甲，但由于产品甲的销售量期望值大于产品乙，使得产品甲产生的边际贡献总额期望值超过了产品乙。另外，从概率分析来看，产品甲销售量超过5 550件的可能性为50％，产品乙销售量超过4 600件的可能性也为50％，因此，两种产品销售量超过期望值的可能性相同，即销售两种产品的风险相似。在这种情况下，应选择边际贡献总额期望值大的方案，即生产新产品甲较为有利。

【例6-15】威利公司正在开发一种新产品，该产品的寿命期为一年，主要针对一个市场，预计其市场价格为26元。经初步市场调查，公司估计该产品年销售量可达到30 000件，这个数量在企业正常生产能力范围之内。该产品最悲观的估计销售量为24 000件，最乐观的估计销售量为36 000件。

该产品的成本估计如下：单位变动成本为12元，其中直接材料5元，直接人工和变动制造费用7元；全年固定成本为170 000元；与企业正常生产能力比例有关的半变动成本如表6-37所示。

表6-37　半变动成本与正常生产能力的关系

公司如果不生产新产品，则可继续生产老产品，年获利为120 000元。由于老产品是销售给既定的现有顾客，因而这120 000元的营业利润是确定的。

要求：

（1）分别计算销售量为24 000件、30 000件和36 000件时的营业利润。

（2）根据进一步的市场调查，上述三种销售量的概率分别为：24 000件的概率为0.3，30 000件的概率为0.5，36 000件的概率为0.2。另外，单位产品直接材料又因材料价格的变动有两种可能，其金额和概率为：5元的概率为0.7，6元的概率为0.3。用概率分析法计算营业利润期望值，并根据概率对结果进行分析。

分析过程如下：

（1）分别计算三种销售量的营业利润。

首先确定三种销售量所对应的半变动成本。因为正常生产能力（100％）的销售量为30 000件，其对应的半变动成本应为115 000元；销售量24 000件是正常生产能力的80％，其对应的半变动成本应为100 000元；销售量36 000件是正常生产能力的120％，其对应的半变动成本应为130 000元。然后分别计算三种销售量的营业利润如表6-38所示。

表6-38　三种销售量的营业利润　单位：元

（2）概率分析

如果材料价格上涨导致直接材料由5元上升至6元，变动成本也将上涨，利润将下降。当直接材料上升至6元时，每单位产品直接材料成本增加1元，则三种销售量下的营业利润计算如表6-39所示。

表6-39　直接材料为6元时三种销售量的营业利润　单位：元

根据销售量的三种可能性以及直接材料成本的两种可能性，可以组成六种销售组合。在这六种销售组合中，每一组合的概率称为联合概率。计算出不同销售组合的营业利润，然后用每一销售组合的联合概率进行加权平均从而计算出营业利润期望值。每一销售组合的联合概率计算如表6-40所示。

表6-40　联合概率的计算

根据表6-40中六种销售组合的营业利润及联合概率，计算销售新产品的营业利润期望值，如表6-41所示。

表6-41　营业利润期望值的计算

由表6-41可见，开发新产品的营业利润期望值为119 280元，与目前老产品的营业利润120 000元相差无几，因而该方案的选择主要取决于决策者对待风险的态度。

如果以目前120 000元营业利润为衡量标准，大于120 000元的可能性为55％。特别是如果销售量达到最大36 000件，而直接材料为最低5元时，可获得204 000元的最大营业利润，联合概率表明出现这个结果的可能性为14％。风险偏好者可能会选择开发新产品。

然而，采纳该方案后，营业利润低于66 000元的可能性也达到30％，而66 000元利润几乎只有正常利润的一半。风险回避者可能会拒绝此方案，而继续生产老产品，以保证稳定获得120 000元的营业利润。

由此可见，在不确定的情况下，运用概率分析能够帮助企业决策者确定决策结果出现的范围以及出现的可能性，从而有助于决策者在风险和无风险两者之间做出选择。