理论模型：国内外价格、工资率、转移支付、政治影响和决策

考虑这样一个国家，该国家中的所有劳动人口，数量为L，都拥有相同的偏好，但是他们的要素禀赋却不同。每个人的拟线性效用函数为：

这里的c0是基础商品0的消费量，则ci代表商品i的消费量，i＝1，2，…，n。假设商品0的国际和国内价格均为1。ui可微、递增且是严格凹函数。设pi是第i种商品的国内价格，考虑垄断竞争市场的性质，第i种商品的需求满足：

其中，Di为商品i的总需求量。假设每个人的支出水平为E，则间接效用函数为：

其中，p＝（p1，p2，…，pn）为价格向量。而定义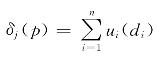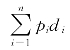－为消费者剩余，di为个人消费量。根据罗尔恒等式，∂δj／∂pi＝－di。

在产品供给方面，假设基础商品的生产只需要劳动力的投入，且投入产出系数为1，劳动力市场是完全竞争市场，工资率为1。每一种非基础商品的生产则需要劳动以及一种专有要素的投入。由于各部门间劳动力作为共同生产要素是可以完全自由流动的，所以各部门的工资率仍为1。假设劳动力以及特殊要素都是无弹性供给，且生产的规模报酬不变。因此，非基础商品i的产量是一个里昂惕夫生产函数：

其中，f表示生产非基础商品的成本函数，ki，li，xji则代表i产品生产中所需要的资本，劳动力和作为中间品的j部门产品。显然，考虑中间品投入的各部门利润可以表示为：

其中，Δji表示一单位i产品所需要的中间产品j的数量。产品i的进口量为mi＝Di－yi＋。产品i的进口关税收入则为Ti＝为对i商品的进口关税。假设政府通过转移支付将关税收入平均分配给每一个人。则个人的间接效用函数就可以改写为：

该表达式中的sji表示为每个人在第i种商品生产的利润中所占的份额。

考虑政府的目标函数：

该式中，W＝LV代表的是社会总福利。ζ代表那些拥有被组织起来的利益集团的行业部门集合。这一假设来源于Olson（1965）所提出的“集体行动”的概念。行业中的一些厂商可能由于拥有共同的利益目标而组织起来形成利益集团，并且采取一致的行动，而那些没有组织起来的厂商由于没有克服“免费搭便车”无法通过一致的行动来影响政府的决策。PCi代表国内各行业利益集团产生的政治影响。结构参数a则是政府相对于利益集团影响赋予社会福利的权重，显然，a＞0。(www.xing528.com)

政府和利益集团之间展开一个两阶段非合作博弈。第一阶段，各利益集团视政策给定进行决策，即max Wi—PCi，Wi为利益集团的收益，一阶条件则为δWi／δti＝δPCi／δti。第二阶段，政府根据利益集团的影响来决定关税，一阶条件为δGi／δti＝0。联合双方的决策，可以得到：

将Wi，W分别展开，通过该式可以得到：

上式中，αζ表示国内利益集团人数与总人口的比；εi表示i产品的进口价格弹性；Ii是一个虚拟变量，如果某行业存在影响政府的国内利益集团，则该变量为1，反之则为0。由于αζ均大于0，因此可以得到以下命题：

命题1：如果某行业中存在可以影响政府的利益集团，即Ii＝1，则该行业将会获得较高的贸易保护。如果该行业不存在可以影响政府的利益集团，即Ii＝0，则政府对该行业的保护较少。

命题2：如果某行业的下游行业中存在可以影响政府的利益集团，即Ij＝1，则该行业获得较少的贸易保护。

命题3：如果某行业的下游行业中不存在可以影响政府的利益集团，即Ij＝0，则该行业获得较高的贸易保护。

根据上文定义，对于结构参数a，αζ可以做出以下推论：

推论1：若αζ＜20%，利益集团是由社会总人口中的少数阶层组成。