多种资源按比例生产一种产品

多种资源按固定比例（x1：x2…xn=a1：a2…an）进行生产，a1，a2，…，an为生产一个单位的商品所需投入的各种资源量，其产量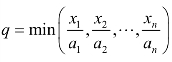。商品的收益与固定资源比例没有关系，商品的收益R=qp，商品的利润π=（q p-c）。

p 为单位商品的价格，分为4 种情况：商品的价格不变，p 为常数；商品的价格递增，以p=kq 为例进行分析（k 为正的纯小数）；商品的价格递减，以p=G-lq 为例进行分析（l 为正的纯小数）；商品的价格递增递减，以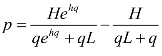为例进行分析。将这4 种价格函数分别乘以产量函数q 得到相应的收益函数：

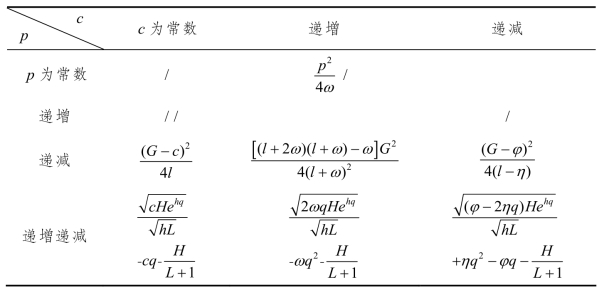
c 为单位商品的成本，分为3 种情况：单位商品成本不变，c 为常数；单位商品成本递增，以c=qω为例进行分析（ω 为正的纯小数）；单位商品成本递减，以c=φ qη-为例进行分析（η 为正的纯小数）。那么，单位商品的利润（p-c）如表8-1 所示。

表8-1　单位商品的利润（p-c）表

续表

将单位商品利润乘以商品量得总利润函数，求总利润关于产量的一阶导数和二阶导数：

（1）商品不变价格和单位商品不变成本构建的总利润函数二阶导数等于零，总利润没有极值（见表8-2）。生产该种商品的利润趋于市场平均利润，产量稳定在一定水平上。

（2）商品不变价格与单位商品成本递减构建的总利润函数二阶导数大于零，商品价格递增与单位商品成本不变、单位商品成本递减构建的总利润函数二阶导数大于零，二阶导数大于零的总利润函数没有极大值，有极小值（见表8-2）。

（3）商品价格与单位商品成本都递增所构建的利润函数二阶导数不确定（本例二阶导数大于零）。如果商品价格与单位商品成本同步递增，总利润函数没有极值。如果商品价格递增快于单位商品成本递增，总利润函数可能有极小值，反之，总利润函数可能有极大值

（4）商品的价格不变与单位商品成本递增构建的总利润函数二阶导数小于零，商品价格递减构建的总利润函数二阶导数小于零，总利润函数有极大值。令一阶导数为零，求解利润最大化的解得q 的值（利润最大化的产量水平），如表8-2 所示。

表8-2　利润最大化的q 值表

价格递增递减与单位商品不变成本构建的总利润函数在满足L＜ehq的条件下有最大值：(www.xing528.com)

价格递增递减与单位商品成本递增构建的总利润函数在满足hhLHehq（L-ehq）＜2ω（ehq+L）3的条件下有最大值：

价格递增递减与单位商品成本递减构建的总利润函数在满足2η（ehq+L）3＜hhLHehq（ehq-L）的条件下有最大值：

价格递增递减构建的总利润函数在满足一定条件下二阶导数小于零，有最大值，最大值用含有产量q 的一元方程表出，在实践中可用插值法求得其解。

当资源量很大，大于表8-2 中最佳产量规模所需的资源量时，表8-2中的q 值是最佳的产量规模。根据q 值可求得各种资源的最佳投入量xi=aiq（i=1，3，…，n）。当资源量较小，小于表8-2 中最佳产量规模所需的资源量时，最大可能的产量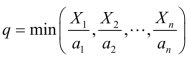，Xi（i=1，3，…，n）为资源限制量。

总成本等于C=cq，那么，各种类型的总成本如表8-3 纵栏标题所示。将表8-2 中的利润最大化的产量q 代入各种类型的总成本（见表8-3）。

表8-3　利润最大化的成本量

总收益等于R=qp，那么，各种价格类型的总收益如表8-4 横栏标题所示。将表8-2 中的利润最大化的产量q 代入各种价格类型的总收益（见表8-4）。

表8-4　利润最大化的收益

总利润等于π=R-C=qp-cp，各种价格类型的总利润如表8-5 所示。

表8-5　利润最大化的利润