两种资源分配对两种生产活动的影响

本节仍然采用上一节的符号界定和收益函数的基本类型，分析两种资源投入量的变化所引起收益变化的规律。资源投入对生产活动的贡献遵循规模报酬递减规律。对于某种生产活动，随着资源投入规模的扩大，资源的边际收益递减，这需要用另外一种资源来替代。资源的边际替代率递减，随着替代资源的扩大资源的替代能力随之减弱，这就要求适度替代。达到资源适度替代的标准是两种有限资源投入收益最大化。

甲乙两种生产活动的收益，既是X 资源投入的比例λx的函数，又是Y资源投入的比例λy的函数。由于X 资源与Y 资源有一定替代性，λx与λy也有一定替代性（见式（7-37）），所以，通过替代公式（7-37）可以把收益只表示成λx的函数。

将式（7-37）代入式（7-19），得

将式（7-37）代入式（7-20），得

这样代换后，X 资源、Y 资源分别对甲、乙两种生产活动收益的贡献都可以表示成X 资源投入比例λx的函数。

对式（7-17）、式（7-18）、式（7-39）、式（7-40）分别求一阶导数和二阶导数：

式（7-47）在0 至1 闭区间λx∈[0，1]是成立的，所以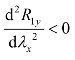为真。

式（7-50）在0 至1 闭区间λx∈[0，1]是成立的，所以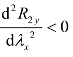为真。(www.xing528.com)

两种生产活动的总收益为：

所以，R 有极大值。

式（7-54）表明：甲产品生产活动的两种资源投入的边际收益之和，等于乙产品生产活动的两种资源投入的边际收益之和，符合这一条件的资源配置能使两种产品的收益之和最大化。

式（7-54）还可变换成：

X 资源投入甲、乙两种产品的边际收益之差，等于Y 资源投入甲、乙两种产品的边际收益之差，符合这一条件的资源配置也能使两种产品的收益之和最大化。

式（7-54）中只有一个未知变量λx，在实践中，代入模型参数值，用插值法可求得λx的值。根据式（7-54）求得λx，可进一步求得两种资源对两种生产活动的分配数量：