等收益线资源价格不变的成本最低点及其轨迹分析

（1）等收益线上成本最低点。如果把生产规模固定在一定水平，也就是把收益水平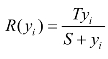确定下来，那么，yi的值也就被确定了——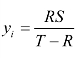（式中R 为人为确定的收益水平）。

在式（6-10）中，如果把yi看成常量，那么，成本就仅是λ的函数。

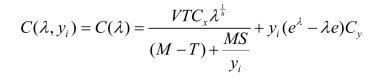
求成本 C（λ）关于λ的导数：

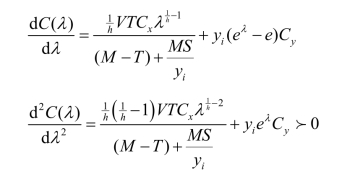
成本函数的二阶导数大于零，符合有极大值的二阶条件。

令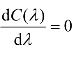，得

适合式（6-12）的λ的值，是既定生产规模的最低成本的解。将λ的值代入得到等收益线上成本最低点的X 资源投入量。将λ的值代入y=yi（eλ-λe）得到等收益线上成本最低点的Y 资源投入量。就这样，在等收益线上至少能找到一点（x，y）为成本最低点。将适合式（6-12）的λ分别代入式（6-10）、式（6-11）得到等收益线上成本最低点的成本和利润。

（2）成本最低点的运动轨迹。

将式（6-12）等量变换：(www.xing528.com)

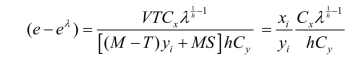
将式（6-5）等量变换：

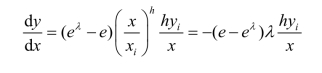
将式（6-12）的等量变换式代入式（6-5）的等量变换式，得

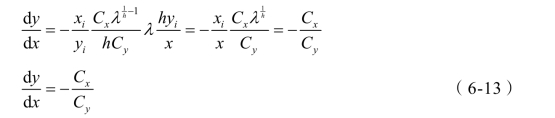
式（6-13）表明：在资源价格不变的条件下，等收益线上成本最低点的切线斜率为负，其绝对值为两种资源的价格之比；切线斜率只与两种资源的价格有关，与其他参数没有关系。所以，等收益线上成本最低点的切线斜率是常数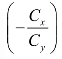，等收益线上成本最低点的切线是一族平行线。这族平行线与等收益线的切点组成的集合就是等收益线上成本最低点运动的轨迹（见图6-4）。下面来寻求这个轨迹的表达式。

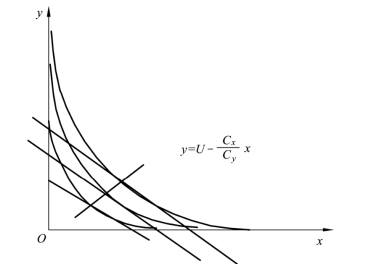
图6-4　等收益线上成本最低点示意图

根据式（6-13），有

在以上积分过程中，U 是积分常数，U 的值标识不同的等收益线。在式（6-14）中，U 是变量，其变化取决于 yi和yi所在等收益线上最低成本点的x。式（6-14）可写成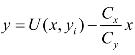。等收益线上成本最低点运动的轨迹用式（6-14）表示（见图6-4）。我们需要在这轨迹上找到最佳生产规模的最佳资源组合点。