等收益线两端点的分析

我们把等收益线与X 轴、Y 轴的交点称为等收益线的端点。等收益线与X 轴的交点（xi，0），表示为获得一定的收益，用X 资源去全部替代Y 资源，相当于只用X 资源进行独立生产，X 资源的投入量为xi。等收益线与Y 轴的交点（0，yi），表示为获得一定的收益，用Y 资源去全部替代X 资源，相当于只用Y 资源进行独立生产，Y 资源的投入量为yi。

等收益线与X 轴的交点的收益和与Y 轴交点的收益相等，即

通过这一等式，可以推导出同一条等收益线的两个端点的关系，即xi与 yi的关系：

等收益线一个端点的位置取决于另一个端点的位置和收益函数的参数。对于式（6-7），如果将等收益线的一个端点（xi，0）固定，将X 资源的收益函数的参数（M和V）固定，那么，等收益线的另外一个端点（0，yi）的位置取决于Y 资源的收益函数的参数（T 和S）。对于式（6-8），如果将等收益线的一个端点（0，yi）固定，将Y 资源的收益函数的参数（T 和S）固定，那么，等收益线的另外一个端点（xn，0）的位置取决于Y 资源的收益函数的参数（M和V）。

因为：xi≻0，yi≻0

所以：Myi+MS-Tyi≻0 ⇒（M-T）yi≻-MS

Txi+TV-Mxi≻0 ⇒(T-M)xi≻-TV

如果M≻T，就有

如果M=T，就有

如果M≺T，就有

因为：x≤xi

所以：

因为：y≤yi

所以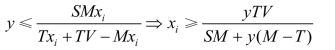：(www.xing528.com)

如果既要满足xi≻0、yi≻0，又要满足x≤xi、y≤yi，就有：

在M≻T 的条件下

在M≺T 的条件下

我们可以只讨论“M≺T”的情形，因为我们总可以设收益极限较大的资源为Y 资源。

从以上推导可知，由于X 资源、Y 资源投入的收益有限，所以等收益线两端点的位置选择也有一定限制。

有了式（6-8），就可证明式（6-5）和式（6-6）。

将式（6-8）代入上式，得

这就证明了式（6-5）。

将式（6-8）代入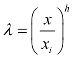，得

式（6-6）在这里得到了证明。

根据前面的约定——，将式（6-8）代入该式得

式（6-9）表明，X 资源的投入量取决于等收益线的位置、形状以及X资源的有效替代与X 资源替代限制量的比例。