固定生产规模下的最优资源配置方案

前面我们把U 看作变量找到了资源最佳组合点式（5-26）与式（5-28）。现在我们把U 看作常量，在等收益线上找成本最低点。

两种资源价格递减，等收益线上任意一点的成本也是在该点两种资源的成本之和，求成本函数式（5-32）的导数：

成本函数式（5-32）有极小值的二阶条件是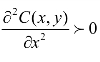。如果满足这一条件，就有

将式（5-44）代入式（5-3），得

式（5-44）与式（5-45）是否是等收益线上成本最低点，还需看它是否满足不等式（5-43）。把式（5-44）与式（5-45）代入式（5-43）并化简得

如果两种资源价格递减的收益函数、成本函数的参数满足以上不等式（5-46），则式（5-44）和式（5-45）是任一等收益线上成本最低点。运用式（5-44）和式（5-45）可计算在一定收益水平条件下的最佳资源组合，进而计算出最低成本和最大利润。

将式（5-44）和式（5-45）代入成本函数式（5-32），得两种资源价格递增的任一等收益线上成本最低点的成本。(www.xing528.com)

一旦收益水平R 确定后，就可以运用式（5-47）计算出该收益水平下的成本。收益水平由生产者确定为R，则在这个确定的收益水平下的利润为π=R-C（x，y）。

如果U 值是变化的，将式（5-37）代入式（5-45）得

将上式进一步简化：

化简的结果得到式（5-38）。同样地，将式（5-37）代入式（5-44），可得到式（5-36）。于是得到如下结论：

如果收益水平是变化的，并且这变化使其U 值达到式（5-37）的水平，那么，就可以运用式（5-44）、式（5-45）和式（5-37）计算两种资源价格递减的最佳生产规模的最佳资源组合。