最佳生产规模下的资源最优配置策略

把 U看成变量，寻找最佳的生产规模及其资源最优化配置点，对式（5-33）求偏导数：

利润函数式（5-33）有极大值必须满足以下二阶条件：

其一，

根据这一条件可推得

Ey是Y 资源利用成本函数的参数，表示资源利用费用达到其极限费用Dy的一半时所利用的资源量；S 是Y 资源利用收益函数的参数，表示Y资源利用收益达到其极限收益T 的一半时所需的资源量。这二阶条件要求Y 资源利用费用达到其极限的一半时所利用的资源量要大于（Y 资源利用）收益达到其极限的一半时所需要的资源量。另外，还要求X 资源的投入量不能为负数。显然，这两个条件能够满足，以下就假设利润函数式（5-33）有极大值的这二阶条件是满足的。

其二，

根据这一条件可推得

其三，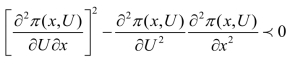

根据这一条件可推得

比较式（5-35）与式（5-34），只要不等式式（5-35）成立，不等式（5-34）就一定能成立。所以，以下只对式（5-35）检验其是否成立。

令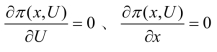：，得以下方程组：(www.xing528.com)

通过整理，得：

等式右边取正，解方程组得：

将式（5-36）和式（5-37）代入式（5-3），得

将式（5-36）和式（5-37）代入式（5-35），得

如果式（5-39）成立，则式（5-36）和式（5-37）是利润函数式（5-33）有极大值的解，式（5-36）和式（5-38）是资源利用价格递增的两种资源联合生产的最佳规模的最佳资源组合点（x，y）。这一点的成本、收益和利润如下：

将式（5-36）和式（5-38）代入式（5-32）得最佳生产规模的最佳资源组合的成本：

将式（5-37）代入式（5-6）得最佳生产规模的最佳收益：

式（5-41）减去式（5-40）得最佳资源组合的利润：

式（5-40）、式（5-41）和式（5-42），分别表示两种无交互作用的资源优化配置（在资源利用边际费用递减的条件下）的成本、收益和利润，从资源利用边际费用递减这一侧面回答了本章开头提出的问题。