固定生产规模下的资源最优分配策略

我们再把U 看成常量，去寻找等收益线上的资源最优配置。

把U 看成常量，等收益线的位置是确定的，收益水平是确定的，那么，等收益线上利润最大化点也就是成本最低点。把U 看成常量，式（5-7）就是利润关于X 资源投入的函数，式（5-7）就可写成

求利润函数的最大值等于求成本函数 C（x，f（x））=xCx+f（x）Cy的最小值。通过求成本函数的最小值，寻找等收益线上成本最低点的资源组合。

在任一条等收益线上，有成本最低点。

证明：

在等收益线上，任意一点的成本为

求成本关于x 的导数，得

把式（5-4）代入上式，得

这符合一元函数有极小值的二阶条件，所以，C（x，f（x））=xCx+f（x）Cy有极小值。

令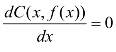，得

解这个方程，得

当收益水平确定之后（收益水平不再是x 和y 的函数，而是一个人为确定的量R），U 的值也就确定了。根据式（5-6），得(www.xing528.com)

把以上两式代入式（5-3），得

经整理，得

式（5-14）和式（5-15）是任一等收益线上成本最低点的X 资源与Y资源的投入组合，这种组合是利润最大化的组合。一旦收益水平R 确定后，就可以用式（5-14）和式（5-15）计算出X 资源与Y 资源的最优配置量。

把式（5-14）和式（5-15）代入 C（x，y）=xCx+yCy，得等收益线上成本最低点（也是利润最大化点）的成本：

经整理，得

把式（5-16）代入 π（x，y）=R（x，y）-C（x，y），得

等收益线上成本最低点（也是利润最大化点）的利润：

在式（5-14）、式（5-15）、式（5-16）和式（5-17）中，假定 R（x，y）是一个确定的量，是人为确定的收益水平（或生产规模）。在 R（x，y）已知的条件下，运用式（5-14）和式（5-15）安排资源的最优配置，运用式（5-16）和式（5-17）求得优化配置资源的成本和利润。如果R 不是一个确定的量，是一个变量 R（x，y），那么，资源优化配置点及其最低成本和最大利润也就随之变动而变动。如果 R（x，y）变化达到式（5-11）的最佳规模时，运用式（5-14）、式（5-15）、式（5-16）和式（5-17）所计算的值就是最佳规模的资源最优配置及其最低成本和最大利润。

把式（5-11）代入式（5-14），得

这一结果就是式（5-9）。同样地，把式（5-11）代入式（5-15），得到式（5-10）；把式（5-11）代入式（5-16），得到式（5-12）；把式（5-11）代入式（5-17），得到式（5-13）。也就是说，最佳生产规模的资源最优配置及其最低成本和最大利润，可以根据收益水平达到最佳值（运用式（5-14）、式（5-15）、式（5-16）、式（5-17））来计算。