最优资源配置：如何掌握最佳生产规模？

我们首先把U 看成变量，去寻找最佳生产规模的资源最优配置。

把U 看成变量，等收益线的位置是不确定的，那么，我们需要找到利润最大化的一条等收益线而确定U 值，又在这条线上找到利润最大化（或成本最低）点（x，y）而确定X 资源和Y 资源的投入组合。

对式（5-7）求 π（x，f（x，U））的偏导数

将式（5-5）代入上式，得

将式（5-4）代入上式，得

式（5-7），是 π（x，f（x，U））关于x 和U 的二元函数，有极大值，因为：

，，符合二元函数有极大值的二阶条件。所以，π（x，f（x，U））=M+T-MVUTS-xCx-f（x，U）Cy有极大值。

通过整理，得

解这个二元方程组，得

再把这组解等量变换，得

将上式代入式（5-3），得

通过整理，得

式（5-8）、式（5-9）和式（5-10）就是我们所寻找到的“两种资源（价格不变）联合生产达到利润最大化时的最佳生产规模和最优资源配置”。(www.xing528.com)

运用式（5-8）计算U 的最优值，表示最佳生产规模的U 值。U 的最优值用两种资源独立生产时的收益函数的参数和两种资源的价格表示。把式（5-8）等量变换成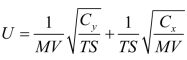，可明显看出，最佳生产规模时的U 值，与资源价格成正比，与收益函数的参数成反比，（0，1）U ∈。最有实用价值的是式（5-9）和式（5-10），给出了最佳生产规模的最优资源配置，运用式（5-9）和式（5-10）分别计算最佳生产规模的X 资源投入量和Y 资源投入量。把式（5-9）等量变换成x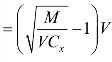，M是X 资源投入的收益极限量，VCx是X 资源投入的收益达到极限量的一半时的成本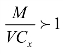，。同样地，把式（5-10）等量变换成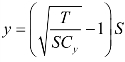，T是Y 资源投入的收益极限量，SCy是Y 资源投入的收益达到极限量的一半时的成本，。

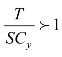把式（5-8）代入式（5-6），得

经整理，得

运用式（5-11）计算收益函数 R（U）的最优值，表示两种资源（价格不变）联合生产的最佳生产规模。

把式（5-9）和式（5-10）代入 C（x，y）=xCx+yCy，得

经整理，得

运用式（5-12）计算最佳生产规模的最低成本。这个成本是资源最优配置时的成本。

把式（5-11）和式（5-12）代入π（x，y）=R（U）-C（x，y），得

经整理，得

运用式（5-13）计算资源优化配置的最大利润，这个利润是最佳生产规模的最大利润。

式（5-11）、式（5-12）和式（5-13），分别表示两种无交互作用的资源优化配置（在资源价格不变的条件下）的收益、成本和利润，从资源价格不变这一个侧面回答了本章开头提出的问题。