把U 看作常数，等收益线的位置也就固定下来，则式（5-3）就是等收益线上点（x，y）运动的轨迹方程，表示用两种资源（X 资源和Y 资源）联合生产时X 资源与Y 资源的替代关系。
把式（5-3）带入式（5-2），得y 关于x 的导数：
式（5-4）中，
表示X 资源对Y 资源的边际替代率，这个边际替代率是变化的（随着X 资源投入量x 的变化而变化），是x 的函数。在等收益曲线上，这个边际替代率表现为等收益曲线上任意一点的切线的斜率，这个切线的斜率为负。如图5-1 所示。
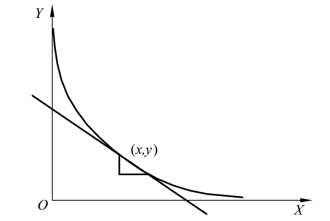
图5-1 边际替代图
把U 看成变量，等收益线的位置就是变动的，Y 资源的投入量y 取决于X 资源的投入量x 和等收益线的位置U，y 是关于x 与U 的二元函数，
。X 资源的改变量Δx 和等收益线位置的改变量ΔU 都可能引起Y 资源投入量的改变。(www.xing528.com)
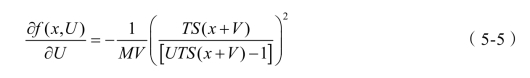
式（5-5）表示：X 资源投入量不变，由等收益线位置的改变量ΔU 与于其所引起的Y 资源投入量的改变量Δy 的比率（即
）。这个比率的大小取决于规模报酬增（或减）的程度，将影响生产者生产规模的选择，是适度生产规模的依据。
等收益曲线的位置发生改变，意味着收益水平发生了改变，如果不改变X 资源的投入量，就要改变Y 资源的投入量，或者X 资源的投入量、Y资源的投入量都改变，如图5-2 所示。这时，资源的边际替代率可以发生变化，也可以不发生变化。图5-2 中，不同位置的两条等收益线的切线分别切于A 点和C 点，如果这两条切线平行，从A 点到C 点，收益水平发生了改变、X 资源的投入量发生了改变、Y 资源的投入量发生了改变，但边际替代率没有发生改变。图5-2 中，B、C、D 是同一等收益线上的点，从A 点到B 点，收益水平发生了改变、Y 资源的投入量发生了改变、边际替代率发生改变，但X 资源的投入量没有发生改变；从A 点到D 点，收益水平发生了改变、X 资源的投入量发生了改变、边际替代率发生了改变，但Y 资源的投入量没有发生改变。
图5-2 等收益线变动图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
