两种资源生产一种商品，两种资源之间有一定的互补性和替代性，这两种资源需要联合生产才能提高效益。但是，我们为了考察两种资源分别对生产的影响，首先固定一种资源的投入不变，去观察另一种资源投入变化对生产的影响。这相当于把两种资源独立开来，分别进行生产活动。如果只考察X资源进行的生产，生产中所需要的Y资源完全用X资源代替（假设规模报酬是递减的），那么加大X 资源的投入，X 资源对Y 资源的替代能力也就越来越弱。如果只考察Y 资源进行的生产，生产中所需要的X资源完全用Y 资源代替，那么加大Y 资源的投入，Y资源对X资源的替代能力也就越来越弱。
选择X 资源单独生产的收益 R（x）关于资源投入量x 的函数为
式中M是收益的极限值，V 是收益达到极限值的一半时X 资源的投入量。
选择Y 资源单独生产的收益 R（y）关于资源投入量y 的函数为
式中T 是收益的极限值，S 是收益达到极限值的一半时Y 资源的投入量。
（1）资源的价格不变。
如果资源的价格不变，X 资源的价格为cx，Y 资源的价格为cy，那么X 资源和Y 资源的利润函数如下。
首先分析利用X 资源进行生产的利润函数：
求利润关于X 资源的一阶导数，并令其为零，得到利润最大化时的资源投入量x0。（用x0表示最佳的X 资源投入量，以区别于一般的X 资源变量x。同样地，用 y0表示最佳的Y 资源投入量。下同）
把式（4-84）代入式（4-80）得到利用X 资源生产的最佳收益。
把（4-84）代入（4-83）得到利用X 资源生产的最大利润。
同理，利用Y 资源进行生产的利润函数的分析：
利润最大化时的资源投入为：
Y 资源生产的最佳收益为：
Y 资源生产的最大利润为：
（2）资源价格递增。
如果资源有限，生产规模扩大，对资源的需求增加，资源的价格就会增加。资源价格随着资源量的利用增多而递增，资源成本函数就是严格凹函数。前面列出的收益函数是凸函数，现在通过这个凹函数和凸函数来分析利润函数。
首先分析利用X 资源进行生产的利润函数。设X 资源限量为X，X 资源被利用一半时的资源成本为Bx，则资源成本函数为：
利润函数为：(www.xing528.com)
求利润关于X 资源投入函数的导数，并令其一阶导数为零，求得利润最大化时的资源投入量。
将式（4-94）代入式（4-80）（经整理）得到最佳收益为：
将式（4-94）代入式（4-92）得到利润最大化时的资源成本为：
将式（4-92）和式（4-93）代入 π（x）=R（x）-C（x）得最大利润为：
同理，分析利用Y 资源进行生产的利润函数。设Y 资源的限量为Y，Y 资源被利用一半时的资源成本为By，则：
（3）资源价格递减。
如果资源无限，资源投入规模报酬递增，生产规模扩大，对资源的需求增加，资源的价格有可能降低。资源价格随着资源利用量的增多而递减，那么资源成本函数就是严格凸函数。前面列出的收益函数是凸函数，现在通过这个（收益）凸函数和（成本）凸函数来分析利润函数。
首先分析利用X 资源进行生产的利润函数。设该项生产活动的总成本极限为xD，设成本达到极限成本的一半时资源投入量为Ex，则资源价格减少的总成本函数为：
利润函数为：
对式（4-105）求x 的导数：
因为M≻Dx，V≻Ex，所以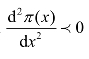
，利润函数 π（x）有极大值。
令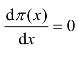
，得
求解x 得
利润最大时的收益为：
利润最大时的资源成本为：
利润最大时的利润为：
同理，设利用Y 资源进行生产活动的总成本极限为Dy，设成本达到极限成本的一半时资源投入量为Ey，则：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
