【摘要】:两种资源的组合比例可以改变的生产活动称为资源可替代的生产。在这里,资源的比例是变动的,收益是关于X资源投入和Y 资源投入的二元函数,R=R(x,y),我们把这个二元函数放到三维向量空间OXYR 中去进行研究。图4-9收益与资源投入坐标图直角坐标平面OXY 内的点,用一对有序实数(x,y)表示,代表一种资源组合。OXY 平面的某一区域表示所有可能的资源组合点的集合,这个集合内的点向空间映射,所得到的对应点的集合是一面抛物面。
两种资源的组合比例可以改变的生产活动称为资源可替代的生产。在可替代的生产中,两种资源的比例不是固定的,而是可以变动的。在前面固定比例投入生产中,我们把收益关于资源投入的函数当成一元函数,在坐标平面OKR 内进行研究。在这里,资源的比例是变动的,收益是关于X资源投入和Y 资源投入的二元函数,R=R(x,y),我们把这个二元函数放到三维向量空间OXYR 中去进行研究。我们把每一种资源组合用OXY 平面内的一点来表示,任一资源组合点在三维向量空间OXYR 中能找到一点与之对应,空间中的这一点到OXY 平面的距离(或到对应点的距离)就是这个资源组合所带来的收益R(见图4-9)。
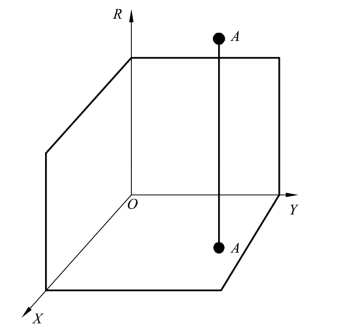
图4-9 收益与资源投入坐标图(https://www.xing528.com)
直角坐标平面OXY 内的点,用一对有序实数(x,y)表示,代表一种资源组合。这一点向空间映射,得到一个空间对应点,这个空间对应点用一组有序实数(x,y,r)表示,代表用资源(x,y)组合进行生产所能带来的收益。OXY 平面的某一区域(或函数的定义域)表示所有可能的资源组合点的集合,这个集合内的点向空间映射,所得到的对应点的集合是一面抛物面(见图4-10)。我们的目的是,要在这面抛物面上找到一个最佳的点作为我们的生产决策。
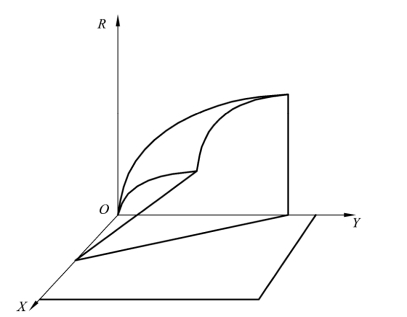
图4-10 资源组合点的空间映射图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




