规模报酬递减：R=R(k)为凸函数的优化方法

如果R=R（k）是凸函数，则生产是规模报酬递减，如图4-7 所示。

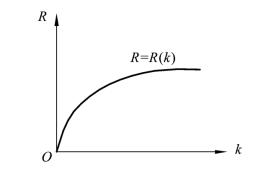
图4-7　凸的曲线

规模报酬递减，如果R=R（ax，ay），就有kR≻R（kax，kay）。导致规模报酬递减的原因可能是：生产规模扩大，商品供应增加，价格降低。资源投入的规模报酬递减，固定比例资源的影子价格是关于资源投入量的单调减函数wxy=wx（ky）。这个函数可能是直线型，也可能是其他单调减函数。

（1）规模报酬匀速递减。

若wxy=f（k）为直线型：

式中n 是直线的斜率，表示减少的收益率与增加的资源投入之比。G为初始值，所对应的收益函数为：

当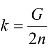时，生产活动有最大收益：

收益最大化的资源投入为：

（2）规模报酬缓慢递减。

若wxy=wxy（r）为曲线型：

G 表示初始值。式（4-33）所对应的收益函数为：

当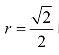时，最大收益为：

收益最大化的资源投入为：

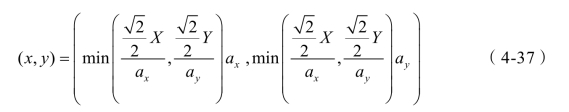
更一般的情况（假定）：

如果将式（4-38）中F 设定为，式（4-38）就变为了式（4-33）的特殊情形。在这里，相应的收益函数为：

当时，有最大收益

(https://www.xing528.com)

收益最大化的资源投入

（3）规模报酬快速递减。

若wxy=wxy（r）为曲线型：

所对应的收益函数为：

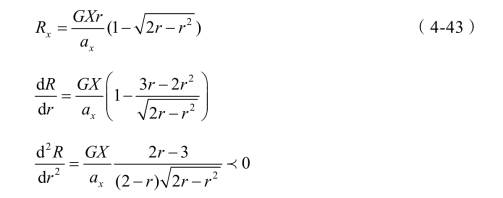
令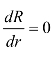，得

符合r∈（0，1）的根有

对于式（4-44）与式（4-43）同样有极大值。

当时，有最大收益为：

收益最大化的资源投入为：

更一般的情况（假定）：

式（4-42）是式（4-47）中的特例。在这里，相应的收益函数为：

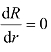令，得

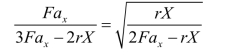
解这个方程有三个根：

取，有最大收益

收益最大化的资源投入为：

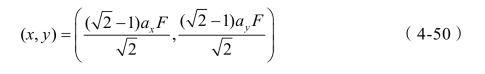
如果，也有相同的结果。