多种生产活动资源最优配置的规模报酬递减趋势

当生产呈现规模报酬递减时，目标函数式（3-27）为凸函数。在3.2.3中我们讨论的两种生产活动的函数曲线同为椭圆轨迹的凸函数，在这里我们研究多种生产活动的函数曲线仍为凸函数，如果这些凸函数仍为椭圆轨迹（见图3-15），与3.2.3 同样——最优的资源配置应使得资源的边际收益在各种生产活动中相等，并等于资源的影子价格，即：

第i 种生产活动的收益关于资源投入的函数为：

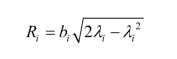
满足式（3-27）的条件是：

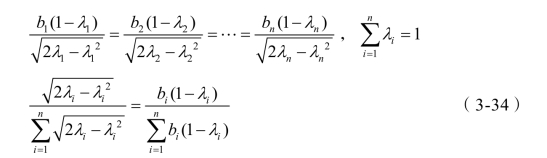
式（3-34）中，bi表示第i 种生产活动的最大收益，是在一定的技术条件下，资源全部投入第i 种生产活动所取得的收益。bi可根据经验或有关技术标准推算而获得。当 bi（i=1，2，…，n）被确定后，可根据式（3-34）求出λi（i=1，2，…，n）也可以近似地用式（3-35）求出 λi（i=1，2，…，n）。

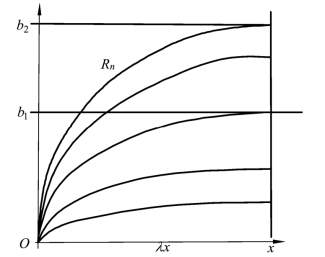
图3-15　多种产出规模报酬递减

如果各种生产函数不是椭圆轨迹，而是其它规模报酬递减函数，是否还是按照前面的方法优化配置资源呢？

资源投入的规模报酬递减，也就是资源的影子价格关于资源投入量的单调减函数——wi=wi（λix）。这个函数可能是直线型，也可能是其他单调减函数。

若wi=wi（λix）为直线型：

式中 ki是直线的斜率，表示单位资源投入，所对应的产出率在减少，减少的收益率与增加的资源投入之比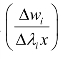。G 为初始值，表示资源开始投入时，单位资源的收率很高，而后随着资源投入的增加而下降。这个直线方程可以根据相关生产理论或历史生产数据模拟回归方程得到。根据式（3-22），与式（3-36）所对应的收益函数为：

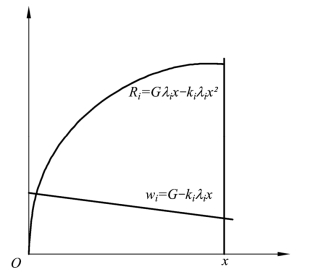
图3-16　直线型规模报酬递减

当时，第i 种生产活动有最大收益（见图3-16）。

如果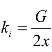，λi=1时，收益 Ri达到最大值。

若wj=wj（λjx）为曲线型：

Bj表示第j 种生产活动的资源投入在起初最高的单位投入产出水平，而后随着资源量的投入增加而降低，这个参数可以通过历史经验或有关理论推导而得到。根据式（3-22），与式（3-38）所对应的收益函数为：(www.xing528.com)

当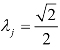时，第j 种生产活动有最大收益（见图3-17）。

图3-17　递减曲线型规模报酬递减

这是约定在资源投入量达到x 时，资源投入的规模报酬为零。如果不是这样，是更一般的情况：

如果将式（3-40）中F 设定为F=x，式（3-40）就变为了式（3-38）的特殊情形。在这里F≠x，相应的收益函数为：

当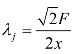时，第j 种生产活动有最大收益。

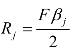若wk=wk（λkx）为曲线型：

Bk和前面Bj的意义一样。根据式（3-22），与式（3-42）所对应的收益函数为：

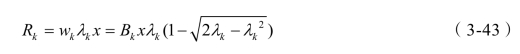
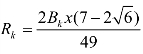当时，第k 种生产活动有最大收益（见图3-18）。

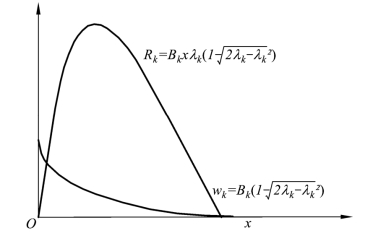
图3-18　递减曲线型规模报酬递增

更一般的情况：

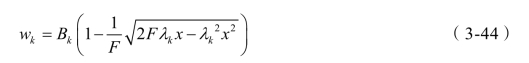
式（3-42）是式（3-44）中F=x 的特例。在这里F≠x，相应的收益函数为：

当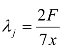时，第j 种生产活动有最大收益。

如果在一组生产活动决策中，包含了以上生产函数或其他规模报酬递减函数，有限的资源分配给各种生产活动的比例——按照各种生产活动的影子价格都相等来计算，即根据式（3-46）求得各种生产活动分配资源的比例。

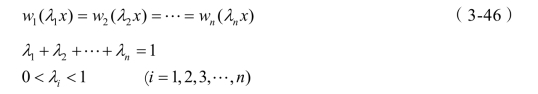
解式（3-46）得各种生产活动最佳利用资源的比例。