资源多用途模型：一种为多种生产活动进行资源安排的方法

进一步的可以将生产活动由两种扩展到多种，分析的结果可以由前面的两种产出扩展到多种产出，资源优化配置在两种生产活动的基础上，用相似的方法分配。假设商品的总数为n，q=（q1，...，qn）为产出向量，p=（p1，...，pn）为价格向量，a=（a1，...，an）为技术参数向量，w=（w1，w2…wn）为影子价格向量，λ=（λ1，λ2…λn）为各种生产活动所用资源占总资源的比例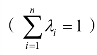，R=（R1，R2…Rn）为收益向量，x 为资源供给的数量。这些向量之间的关系如下：

生产一个单位的商品所需资源的数量ai与该种商品生产的数量qi之积就是生产该种商品投入的资源量。这里仍然把投入多种生产活动的资源总量x 看着是常数，投入到某种生产活动的资源量也等于资源总量与分配比例之积，见式（3-20）。

商品的价格与该种商品的生产数量之积等于其生产活动的收益，用式（3-21）表示。生产活动的收益也可以用资源投入量与相应的影子价格之积来表示，见式（3-22）。

价格向量和影子价格向量是资源配置的重要依据，价格与影子价格之间的关系为：商品的价格除以生产每单位商品所用的资源数量等于影子价格，见式（3-23）；每单位资源投入的产出水平即影子价格，乘以生产每单位商品所用的资源数量，等于价格，见（式3-24）。

各种生产活动的收益之和（即总收益）可以用价格与产量之积、之和来表示，也可以用资源投入量与影子价格之积、之和来表示，见式（3-25）。(www.xing528.com)

资源优化配置的生产活动以收益最大化为目标，其目标函数见式（3-26）和式（3-27）。

式中 V（x）表示的是x 所能生产的所有产出组合的集合。

有了以上这些约定以后，仿照3.2 节的方法，对规模报酬不变、规模报酬递增、规模报酬递减等生产活动的资源优化配置问题进行研究。