最优资源配置下的规模报酬递减问题

甲、乙两种生产活动，都呈现资源投入的规模报酬递减，与前面一样——仍然选择椭圆方程进行分析，椭圆以 B（x，0）为圆心（见图3-8）。甲乙两种生产活动的收益与资源投入的椭圆方程：

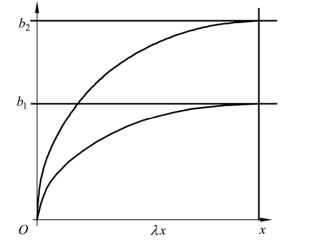
图3-8　两种产出规模报酬递减

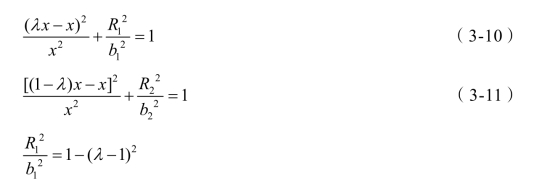
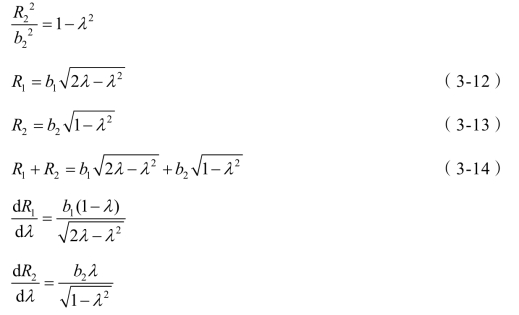
在λ∈[0，1]，当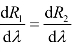时，R1+R2有最大值。

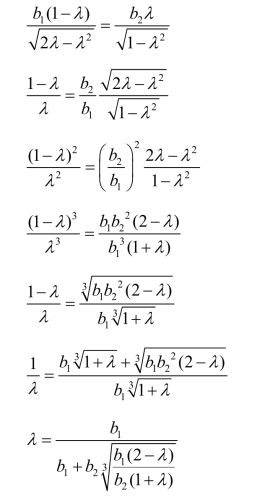
当 b1=b2时，，式（3-14）有最大值。当 b1＜b2时，，式（3-14）有最大值。当 b1＞b2时，，式（3-14）有最大值。在 b1≠b2时，可近似地取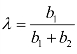。在式（3-14）中，λ∈[0，1]，。λ在取值区间内，对应的总收益值列入表3-17。

表3-17　规模报酬递减的资源投入组合收益表(https://www.xing528.com)

从表3-17 看出：

如果 R1（x）=R2（x），即甲乙两种生产活动的最大收益相等，有限的资源平均配置两种生产活动能使总收益值达到最大值，生产决策——两种生产活动等量投入资源。如果 R1（x）≠R2（x），即甲乙两种生产活动的最大收益不相等，资源平均配置两种生产活动或只配置一种生产活动都不是最佳选择。资源配置的比例为：甲商品生产资源投入的比例等于甲商品生产的最大收益值比上甲已两商品生产的最大收益值之和；乙商品生产资源投入的比例等于乙商品生产的最大收益值比上甲已两商品生产的最大收益值之和。

当生产呈现规模报酬递减时，两种生产活动的收益函数分别为：

总收益为：

求关于λ的导数可以得出使得总收益最大化的资源配置。两种都具有规模报酬递减的生产活动，有限的资源按两种生产活动的生产潜力配置，生产潜力大的多投入资源，生产潜力小的少配置资源。