资源最优配置实现规模报酬递增

生产甲、乙两种商品所投入的资源量为x，在本章，我们把x 看作个常量，在资源限制条件下讨论具有规模报酬递增的两种生产优化配置资源。假设甲乙两种生产的收益（R1和R2）与资源投入的函数都是同类型的连续递增函数，选择椭圆方程为基本函数，椭圆的长轴为x、短轴为bi（i=1，2）、椭圆的圆心为B（0，bi）。如图3-7 所示，我们只讨论第一象限内的函数。生产甲乙两种商品的椭圆方程的长轴均为x，表示生产甲商品（或乙商品）的资源投入量的选择范围，生产甲商品的资源投入量 λx，生产乙商品的资源投入量（1-λ）x，λ∈[0，1]。生产甲商品的椭圆方程的短轴均为b1，b1=R1（x），表示全部资源生产甲商品的最大产出量。生产乙商品的椭圆方程的长轴均为b2，b2=R2（x），表示全部资源生产乙商品的最大产出量。生产甲乙两种商品的椭圆方程为：

图3-7　两种产出规模报酬递增

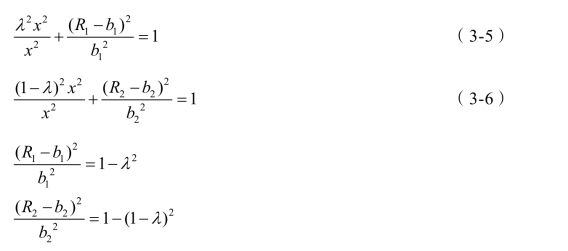
从式（3-9）看出，在生产函数确定之后，两种生产活动的收益之和取决于，λ∈[0，1]：

λ取不同的值，两种生产活动的资源投入就有不同的组合，也就有不同的收益。我们选择能使收益达到最大化的那一组资源组合作为生产决策。表3-16 列出了λ取不同的值所对应的总收益。(www.xing528.com)

表3-16　规模报酬递增的资源投入组合收益表

从表3-16 中看出：

如果 R1（x）=R2（x），即甲乙两种生产活动的最大收益相等，一种资源投入尽管生产的商品不一样，但产生的经济效果是一样的。资源分散投入两种生产活动（不管怎样的组合）的收益不如集中投入一种生产活动的收益高，生产决策——将全部资源只投入甲商品的生产或只投入乙商品的生产，不同时用于生产两种商品。如果 R1（x）＜R2（x），即甲商品生产的最大收益小于乙商品生产的最大收益，不管怎样的资源投入组合，都不会超过乙商品生产的最高收益，生产决策——全部资源投入乙商品的生产。如果 R1（x）＞R2（x），即甲商品生产的最大收益大于乙商品生产的最大收益，不管怎样的资源投入组合，都不会超过甲商品生产的最高收益，生产决策——全部资源投入甲商品的生产。

当生产呈现规模报酬递增时，生产函数为凸函数。凸函数的极值点位于函数定义域的边界上。目标函数为：

恒有R=R1+R2≤R1（x），或者R=R1+R2≤R2（x）。两种都具有规模报酬递增的生产活动，有限的资源全部投入规模报酬较高的一种生产活动。这与3.1.4 的结论相同。