【摘要】：甲产品规模报酬递增与乙产品规模报酬递减构建的收益函数，乙产品规模报酬递增与甲产品规模报酬递减构建的收益函数，这二者是对称的。表3-13～表3-15 的“λ”栏是收益函数一阶导数为零的方程，该方程符合收益函数二阶导数小于零的解为收益最大化的解。如果规模报酬递增的速度大于规模报酬递减的速度，全部资源投向规模报酬递增的生产活动。
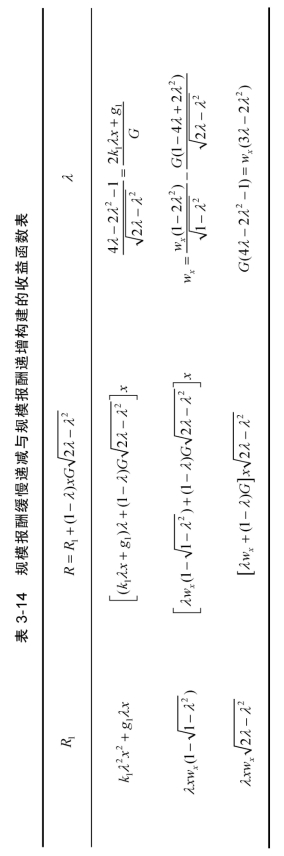
甲产品规模报酬递增与乙产品规模报酬递减构建的收益函数，乙产品规模报酬递增与甲产品规模报酬递减构建的收益函数，这二者是对称的。因此，我们这里只讨论甲产品规模报酬递增与乙产品规模报酬递减构建的收益函数。这类收益函数的二阶导数的正负号需根据模型的参数来确定。如果二阶导数大于零（或者等于零），同前一样，两种资源只投向一种生产活动。如果二阶导数小于零，令一阶导数为零求解λ，由λ和（1-）λ决定资源分配。由规模报酬快速递增、快速递减所构成的收益函数在定义域【0，1】内既有极大值又有极小值，我们只讨论极大值部分。表3-13～表3-15 的“λ”栏是收益函数一阶导数为零的方程，该方程符合收益函数二阶导数小于零的解为收益最大化的解（见图3-6）。
(www.xing528.com)
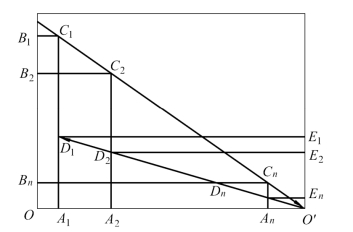
图3-6 资源配置定分比点示意图图
在图3-6 中：约定规模报酬递增的速度小于规模报酬递减的速度。由定分比点 A1所决定的收益为
，由定分比点 A2所决定的收益为
……由定分比点An所决定的收益为
。
在S1与 Sn之间必定有一个最大值（最大收益值）。这个最大值所对应的资源分配定分比点为资源优化配置点。
如果规模报酬递增的速度大于规模报酬递减的速度，全部资源投向规模报酬递增的生产活动。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
