理论依据与基本概念

有限的资源对生产活动的配置形成的资源结构与产品结构之间的关系η=Bη+Iξ+ζ（η表示产品结构，B表示产品之间的关系矩阵，ξ表示资源结构，I表示资源结构与产品结构之间的关系矩阵，ζ表示表示随机误差项）称为资源—产品结构模型。资源对生产活动有不同的配置，就有不同的结构模型。在众多的结构模型中，至少能找到一种优化组合的产品能极大地满足人们的需要（效用最大化）。有限资源的优化配置映射产品优化组合得到多维向量空间的最优点，本书证明了这个最优点的存在性，在理论上推导出了求解这个最优点数学模型，为产业结构调整提供理论支撑和方法论指导。在本书理论推导的过程中，一些主要名词的含义如下：

（1）资　源

本书中的资源是广义的资源，包括不可再生资源、再生资源，还包括生产要素等。新古典经济学把技术变化也作为一种生产要素，用于解释未被传统生产要素所解释的产出增长。在奥地利学派中，企业家精神被作为最重要的生产要素。但在新古典学派中，企业家精神与人力资本并没有本质的区别。本书中的资源不包括技术和企业家精神，本书中的资源主要指生产过程中的实质性的投入，如土地、劳动等物质资源和劳动力资源。

（2）生产函数

在本书中，生产函数是资源投入与产品产出的数量、收益、利润等之间的等量关系（即函数关系）。不同的生产活动有不同的生产函数，不同的资源、不同的资源组合……有不同的生产函数。用y={y1，…，yn}表示产出向量（产品数量或收益），其中n表示产出的种类；用x={x1，…，xm}表示投入资源向量，其中m表示投入资源的种类。则生产函数可以表示为y=f（x）。本书还研究了有约束条件的生产函数。

（3）成本函数

会计学上成本函数是对产品而言，是关于生产成本与产出规模之间的函数关系，表示在每一个产出水平上的生产成本。本书的成本函数是对资源投入而言，是关于生产费用与资源投入规模之间的函数关系。单位资源成本就是资源的价格，资源价格也是资源投入规模的函数，所以，本书把随资源投入规模变化的成本函数称为规模成本。规模成本分三种类型：

① 规模成本不变（资源的价格cp不变），成本等于资源投入的数量x乘以资源的价格（C=xcp）。规模成本不变可能是资源数量相对较大，生产者所用资源数量相对较少，不足以影响资源的供求，资源的价格cp保持不变。

② 规模成本递增（资源的价格cp递增），成本函数是凹函数。式中：x为资源投入的数量；X为资源限制量；B为模型参数，表示资源限制量被用到一半时的资源成本，这个参数可根据生产的性质确定或根据经验模拟。规模成本递增可能是资源有限，资源用量增加，资源的供给减少，资源的价格提高。

③ 规模成本递减（资源的价格cp递减），成本函数是凸函数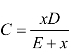。式中：x为资源投入的数量；D为成本限制量；E为模型参数，表示成本达到成本限制量的一半时资源投入量，D、E可根据生产的性质确定或根据经验模拟。规模成本递减可能是资源相对无限，生产规模扩大，由于规模效益，资源的价格就会降低。

（4）收益函数(www.xing528.com)

收益函数是以价值指标描述产出水平与资源投入之间的函数关系。最基本的收益函数是一种资源投入产出一种产品的收益函数，多种资源投入的收益函数或多种产出的收益函数是最基本收益函数的复合或叠加。在一种产出的情况下，从固定的投入获得最大的产出不存在经济上的选择，这一点必定是既定投入水平下生产函数上所对应的点。当产出种类扩大到两种或两种以上时，收益最大化就会变为一个真正的经济决策问题。本书假定资源的边际收益函数递减，基本收益函数为。式中：M为收益极限量；x为资源投入量；V为收益达到收益极限量M的一半时的资源投入量。M和V可根据生产的性质或经验模拟得到。

（5）利润函数

利润函数是以价值指标描述的投入与产出之差，在数值上等于收益减去成本，在形式上由收益函数减去成本函数。收益函数可以表示为R=R（p，y），成本函数可以表示为C=C（w，y），其中p表示产品的价格向量，w表示投入资源的价格向量，y为给定的产出水平。则利润函数π=π（p，w）在形式上可以看作是R（p，y）-C（w，y）。收益函数也可以表示为R=R（px，x），成本函数可以表示为C=C（w，x），其中px表示单位资源的收益向量，w表示投入资源的价格向量，x为给定的资源投入。则利润函数π=π（px，w）在形式上可以看作是R（px，x）-C（w，x）。本书以利润最大化为目标，求解资源最佳投入规模、资源投入最佳结构（生产中投入的资源种类及其比例关系）以及相对应的最佳收益水平和最佳的收益结构（产品收益种类及其比例关系）。收益最大化不等于利润最大化，在资源约束下要求利润最大化，在一种产出的情况下，也存在经济上的决策问题。

（6）规模报酬

在经济学中，规模报酬是指所有投入等比例的变动导致的产出数量的变动。如果产出数量变动的比例大于投入数量变动的比例，则称为规模报酬递增，规模报酬递增的原因是随着生产规模的扩大，投入要素的利用效率提高。如果产出数量变动的比例小于投入数量变动的比例，则称为规模报酬递减，规模报酬递减的原因是投入要素的利用效率随着生产规模的扩大逐渐降低，例如公司规模越大，越难以管理，从而导致资源利用效率的损失。如果产出数量变动的比例等于投入数量变动的比例，则称为规模报酬不变。对于生产函数y=f（x），规模报酬不变意味着λy=f（λx），对任意λ＞0；规模报酬递增意味着λy＜f（λx），对任意λ＞1；规模报酬递减意味着λy＞f（λx），对任意λ＞1。规模报酬通过资源投入的边际收益来反映：边际收益不变，规模报酬不变；边际收益递增，规模报酬递增；边际收益递减，规模报酬递减。资源投入的平均收益与资源投入的边际收益同方向，但滞后。本书采用资源投入的平均收益来反映规模报酬——平均收益不变为规模报酬不变，平均收益递增为规模报酬递增，平均收益递减为规模报酬递减。

（7）影子价格

影子价格表示的是资源最优使用效果的价格，即当资源增加一个单位时，目标函数最大值的增量。影子价格可以反映没有市场价格的商品或者服务的潜在价格，也可以用来反映市场不完善的情况下商品或服务的潜在价格，用于甄别商品或服务的市场价格是否真实地反映了其潜在价格，从而可以得到对市场不完善程度的衡量。

（8）凹函数

凹函数有两种相反的定义：一种定义是函数曲线凸向坐标原点的为凹函数，另一种定义是函数曲线凹向坐标原点的为凹函数。本书采用前者定义。凹函数曲线上任取两点并连线，这条线段高于函数本身曲线的位置。令S表示一个集合，函数g=g（m），对属于集合S中任意两点m和m′，以及λ∈（0，1），如果有g（（1-λ）m+λm′）≤（1-λ）g（m）+λg（m′）成立，则称g=g（m）为凹函数。凹函数意味着边际递增。反之，为凸函数。可以看到，收益函数是凸函数，成本函数是凹函数（一般情况下）。