基于相似性的链路预测算法：实践检验与应用便利性

由于复杂网络在多学科、多领域中的广泛运用，链路预测也相应地得到了更多关注。不同领域的学者从自身领域出发提出了多种链路预测算法，这些算法在计算复杂度和计算效率上存在着些许不同，针对不同的问题，其预测精度也存在差别。确切来说，暂时还尚未有一种普适的链路预测算法，而每一种算法的预测稳定性也需要进一步的实践检验。这也决定了能否将链路预测广泛地应用于实际领域，后续的研究也将进一步摸索其中的规律，以便为链路预测系统性的理论做出贡献。在综合考虑了计算复杂度和实际应用便利性等多个方面后，本节选择基于相似性的链路预测算法作为研究方法。

一、基于相似性的链路预测算法

基于相似度的链路预测方法的实质就是两个节点具有更高的相似性或接近性，那么它们就更倾向于产生链接。这就涉及一个问题，即如何刻画两个节点的相似程度。刻画节点相似程度最简单的方法就是依据节点自身属性，比如两家企业的产品种类、销售额、企业规模等比较接近，就可以说这两家企业比较相似，更倾向于产生链接。在这里，利用节点属性进行链路预测的前提条件是节点之间的链接要代表这种相似性。也就是例子中的企业与企业之间的链接要代表的是它们属于同类企业这种关系。

另外一种刻画节点相似度的方法则抛开属性特征等信息，完全采用网络的结构信息，也就是结构相似性。那么如果结构相似性的定义能符合目标网络结构特征，则结构相似性链路预测精度就相对较高。这种只使用结构信息的链路预测方法计算复杂度较低，简便、实用、高效，如基于共同邻居（Common Neighbors）的相似性指标，它表示两个节点若拥有更多的共同邻居，那么他们就更倾向于产生连边。

具体来分，网络结构相似性还可划分为基于节点信息的相似性指标，基于路径的相似性指标和基于随机游走的相似性指标。

1.基于节点信息的相似性指标

此类指标仅仅依靠节点的相似性信息来进行链路预测，计算复杂度较低，算法效率高，因此也被称作局域算法（Local Arithmetic）。

（1）共同邻居指数CN（Common Neighbor）算法如下：

式中，Γ（x），Γ（y）分别代表节点x，y的邻居节点集合，|Γ（x）|则代表节点x的度，也就是邻居集合中节点的个数。这个指标是最为简单的，对应着两个节点之间共同节点的个数，在实际运用中也具有较好的预测效果，尤其在人际关系领域。同时，这个指标符合人们生活中的经验，比如两个人同时认识的朋友越多，那么这两个人结交成为朋友的概率就越大。

腾讯QQ的“您可能认识的人”这个功能的实现就运用了与这个指数相关的方法，该功能取得了不错的效果。

（2）在共同邻居的基础上，考虑两端节点度造成的影响，从不同的视角又延伸出六种指标，分别为

①Salton指数［1］：

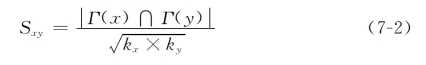
式中，kx和ky分别表示节点x和y的度值，也叫作余弦相似性。

②Jaccard指数［2］：

该指数常用于信息检索的预测。

③Sorensen指数［3］：

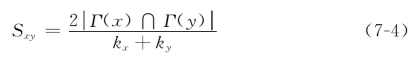
该指数常用于生物群落相似性的比较。

④大度节点有利指数（Hub Promoted Index）：

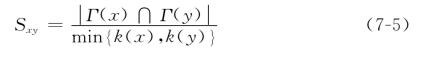
⑤大度节点不利指数（Hub Depressed Index）：

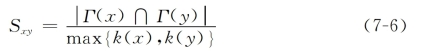
⑥LHN-I指数［4］：

该指数由Leicht，Holme和Newman共同提出，因此命名为LHN。

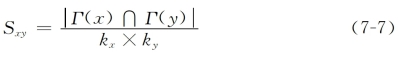
通过以上Sxy的公式可以看出，这6个指数形式相近，只是分析相似性的角度不同，因此适用的领域也稍有差别。

（3）优先连接指数PA（Preferential Attachment）［5］。

优先连接指数因其可以产生无标度网络结构而出名。在网络结构中，一条新边连接到一个节点的概率与该节点自身的度数成正比，即该节点度数越大，那么建立链接的可能性就越高。

该指数由于仅仅需要知道节点度数，计算复杂度相对较低，具有很高的效率，在实际生活中应用较广。

（4）如果考虑到两个节点的共同邻居的度的信息，则有AA和RA指数。两者区别在于给邻居节点赋予权重的形式不同，RA以赋权，AA则以赋权，共同邻居度小时，差别不大，当度值很大时，两者计算的相似性则相差很大。

①AA指数（Adamic-Adar Index）［6］：

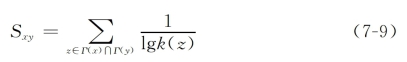
该指数对度小的共同邻居赋予了较大的贡献。

②RA指数（Resource Allocation Index）［7］：

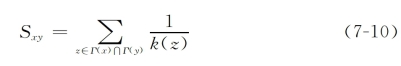
该指数考虑了网络资源分配的情况，即将邻居节点当作资源的中转枢纽，按照自身度值来平均分配资源。

（5）CAR指标［8］。

在考虑共用邻居的度值信息的基础之上，这些共同邻居的相互作用是否对链路预测精度产生影响呢？答案是肯定的，CNL指标正是基于这样的思想。Ravasi等人认为网络倾向于形成某种局部范围内的社团结构，那么针对两个未曾连边的节点对（x，y），用CN（x，y）表示节点对（x，y）的共同邻居个数，用LCL（x，y）表示节点对（x，y）所有共同邻居之间连接边的数目，那么CAR指标被定义为：

该指标明显提高了CN指标的精确度，也超过了AA和RA指数，实际上是增加了相应节点的局部集聚系数，因此对社团结构明显的网络具有很好的预测效果。

2.基于路径的相似性指标(www.xing528.com)

在网络结构中，除了节点外，还有一种形态，即边的存在。那么边是否能作为判断两个节点的相似性的工具呢？答案是肯定的。2个没有共同邻居的节点，通过2条或者更长的路径连接，那么它们的相似性即为基于路径的相似性指数。目前已知的基于路径的相似性指标有局域路径指数、Katz指数、LHN-II指数等。

①局域路径指数（Local Path）［9］。

LP指数除了考虑共同邻居，还考虑了次近邻节点对相似性的贡献，是一种半局域算法，其相似性定义为：

式中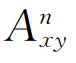，代表着节点x和节点y之间长度为n的路径数目；a为变量且α≥0，控制着次近邻节点能对节点的相似性做出多大的贡献。当α=0时，LP恰好等同于CN指标。

②Katz指数［10］。

在LP的基础上可以继续拓展，考虑四阶路径、五阶路径的贡献，当考虑了所有阶的路径的贡献之后，就得到全局域算法——Katz指数：

式中，Axy为网络的邻接矩阵。假设A的最大特征值为k，当ε＜时，上述数列收敛。

3.基于随机游走的相似性指标

①平均通勤时间ACT（Average Commute Time）［11］。

平均通勤时间代表了从节点x传递到节点y所经过的平均步数，其定义为：

式中，该网络的Laplace矩阵的伪逆矩阵为L+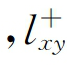表示伪逆阵中相应位置的元素。显然，两个节点的平均通勤时间越小，则这两个节点越接近，可以对其赋予较高的相似性，如式（7-15）所示：

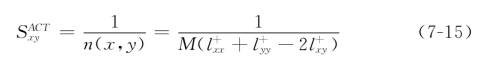
②局部随机游走指数LRW（Local Random Walk）［12］。

LRW指数只考虑有限步数的游走过程，一个粒子在t时刻从节点x出发，在t+1时刻到达节点y的概率为πxy（t），那么系统演变方程为：

式中，πx（0）为一个N×1的向量，第x个元素为1，其余为0。假设：网络中每个节点的初始资源值与节点度值存在正相关关系，即Rx=为节点x的初始资源值，k（x）为节点x的度值，M为常数，那么随机游走t步的LRW相似性定义为：

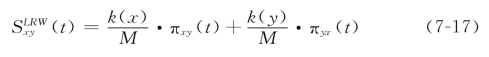
此外，文中还在LWR的基础之上汇总前t步结果，得到SWR的相似性指数，即叠加的局部随机游走指数（Superposed Random Walk）相似性定义如式7-18所示。

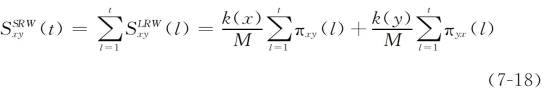
还有一些其他的随机游走类指标。

二、基于相似性预测算法的比较与分析

周涛等给出了基于节点局部信息相似性的指标在蛋白质相互作用网络（PPI）、科学家合作网络（NS）、美国电力网络（Grid）、政治博客网络（PB）、路由器网络（INT）、美国航空网络（USAir）这6个网络中的预测精度，所有结果采用AUC作为预测精度评价指标。张扬夫［13］和白萌［14］也对有关网络进行过验证。本文选取部分常用指数进行汇总整理，实验网络拓扑性质如表7-1所示，网络链路预测精度如表7-2所示。

表7-1 实验网络的拓扑性质表

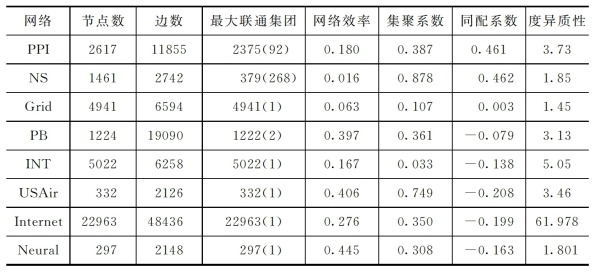
在此，需要指出以下几点：

①由于在测试集和训练集的划分、预测次数等方面，不同研究者使用了不同的数据，而且划分时也存在随机性，不同学者得到的预测精度存在些许差异；

②最大联通集团一列中，2375（92）表示PPI网络中共有92个联通集团，其中最大的联通集团包含节点2375个。

表7-2罗列了基于局域信息的链路预测指标精度，同时也列出了基于路径的链路预测指标精度。可以看出，除了个别网络特例外，采用链路预测算法均可得到比随机连边要好的效果，精度基本都超过0.5，有些指标AUC值还可以达到0.9以上，这表明该项指标对网络结构形态刻画得十分吻合，具有良好的预测效果。

表7-2 实验网络的链路预测精度表

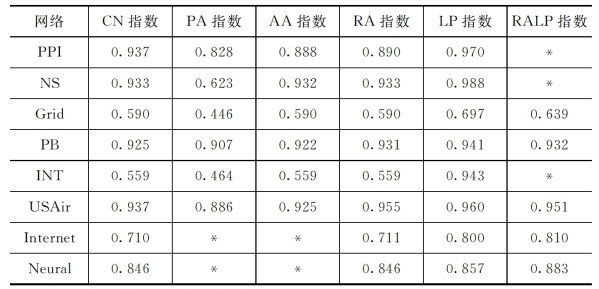
其中，标注*的为未检测该项精度。

由于国内外学者在研究链路预测时，使用的多是以上几个数据集，数量少，且缺乏大量网络数据的实例验证。因此，仅仅通过以上数据，达不到统计上的意义。在此，我们通过对数据进行分析，来简单地推测下这些指标间、拓扑性质间的关系，为后来的研究提供更准确的方向。

由统计分析结果表7-3所示，可以看到（该结果尚缺少大规模数据验证，因此客观地讲，只可以作为参考）：

表7-3 统计分析结果表

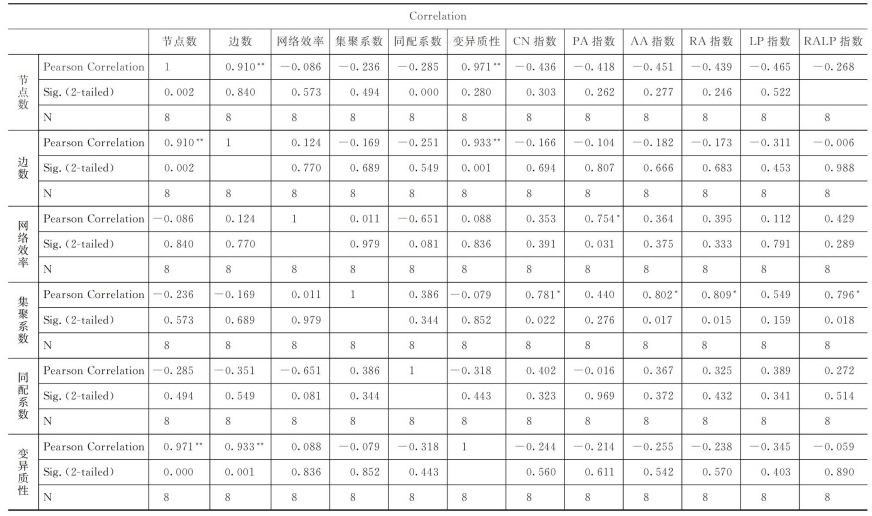
续表

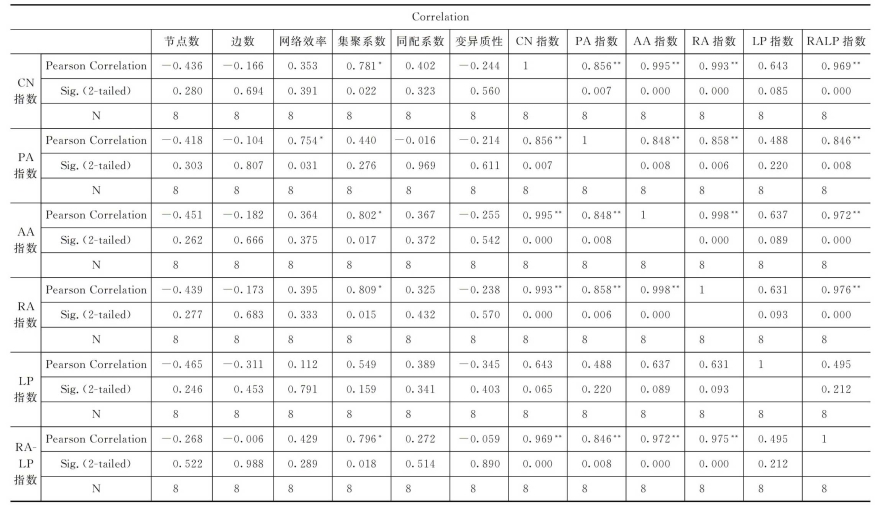
①同配系数与其他各项无明显的相关关系，但是这可能是由于数据有限造成的，或者存在一定的间接关系，而上述结果未进行偏相关分析；

②CN指数、AA指数、RA指数、RALP指数均和网络的集聚系数具有比较明显的相关性，而唯独PA指数表现出了和网络效率具有一定的相关性；

③实验上并没有发现网络同配系数和PA优先连接算法精度上的联系，这也就否定了以往的观念，即认为PA指数对同配网络预测精度不错，对于非同配网络预测精度很差。

通过PA指数的定义可以看出，PA链路预测要想取得高精度，那么需要满足两个条件：一是需要有一定的大度节点；二是大度节点之间或大度节点与其他零散节点之间尚未产生连边。因此，从直观上来看，当网络中出现一定的“明星节点”，形成一些聚类团体时，会更加适用PA算法。

RA指数一方面与共同邻居个数相关，另一方面与共同邻居的度相关。当共同邻居的度值越小时，表示其资源分配时能够转发更多的资源，那么两节点间的相似值就越高，能获得更好的预测精度。同时，Ravasi等人提出的CAR指标也显示出较高的精确度，明显地提高了CN预测精度，也超过了Adamic-Adar指数和Resource Allocation指数。在这里，当共同邻居个数小于或等于2个时，CAR指数和CN指数相同，当网络局部形成社团，集聚系数变大时，那么共同邻居之间的联系更加密切，CAR指数就大大地增加了CN指数的分辨率。与此同时，RA指数由于共同邻居的度值增大，在一定程度上分散了其资源的分配，相似性得分下降。因此，在倾向于形成局部社团的网络中，CAR指数具有比RA指数更高的预测精度。当网络集聚系数小时，RA指数与CN指数分辨能力相差不大，当集聚系数升高时，RA指数就表现得十分出色；但集聚系数升高的过程中会强化CAR指数，而这在一定程度上会弱化RA指数，这也就是在局部社团多的网络中，CAR指数具有比RA指数更好的预测表现的原因。