供应链互联性与强度对抗毁性分析

供应链网络的中断会导致高利润的损失，例如2011年4月中国广州汽车制造业生产总值出现自2003年来的首次下降，同比下降幅度高达32.2%［6］，这是2011年3月日本地震导致的。本章通过供应链网络的连通性和效率来进行抗毁性分析，主要通过攻击强度的调整（总强度不变），攻击方式的选择（随机和蓄意）对节点进行攻击来分析。

一、供应链网络的鲁棒性与抗毁性

鲁棒性是一个可以衡量复杂网络性能的重要指标，它并不是一个全新的概念，在各种各样的网络、系统和组织的研究中，鲁棒性都有它存在的价值，大体可以表示为对事件的承受能力或容错能力，具体如表5-1所示。

从表5-1中对不同类别的鲁棒性定义的列举可以看到，鲁棒性的内涵十分丰富。对于供应链网络而言，鲁棒性是指当不正常的情况，即不符合规则的活动真的发生时，要保证网络不会引起灾难性的后果。

表5-1 鲁棒性定义表

在不同情况下，复杂网络抗毁性的定义是不一致的，但主要由系统定位、威胁、适应性、服务的持续性和时效性这五个部分组成。［7］结合这五个关键的组成要素，可以将供应链网络的抗毁性定义为：当供应链网络中出现随机性或确定性故障，部分节点或子网遭受到自然或人为的摧毁或压制时，该网络能在规定时间内维持及恢复其性能、效能，使其达到一个可接受程度的能力。鲁棒性和抗毁性有相似之处，面对风险的抗毁性在一定程度上反映了网络的鲁棒性。

Albert在《Nature》上发表的文章掀起了研究网络抗毁性的热潮，文章将随机攻击和故意攻击作为破坏网络的手段，主要研究了无权、无向网络的抗毁性，研究表明：在随机攻击下，无标度网络比随机网络有更强的鲁棒性；在故意攻击下无标度网络却非常脆弱［8］。如图5-1所示是一个随机网络，由于没有关键节点（Hub-Node）的存在，这种网络的一个突出特点就是抵抗故意攻击的能力较强，即由于占据重要地位的关键节点（Hub-Node）较少，所以即使移除一部分也不至于使得网络瘫痪。而无标度网络则不同，如图5-2和图5-3所示，BA网络中便存在度很大的关键节点（Hub-Node）。这种服从幂律分布的网络对随机攻击呈现鲁棒性，但当承受对于关键节点针对性较强的外来攻击时，网络则易受较大破坏。

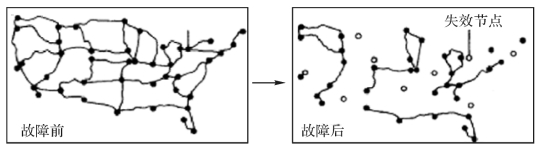
图5-1 ER网络面对随机攻击图

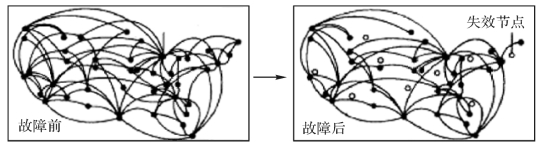
图5-2 BA网络面对随机攻击图

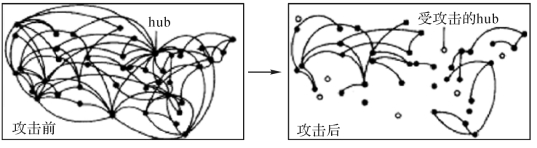
图5-3 BA网络面对选择攻击图［9］

资料来源：BARABASI AL，BONABEAU E.Scale-free networks［J］.Scientific American，2003，5（1）：60-69.

本文参照这两种攻击类型来研究层次型供应链网络模型的抗毁性，并以攻击总权重固定，攻击次数为变量的手段来分析网络的鲁棒性特征，然后提出相应的应对方案。

二、供应链网络抗毁性攻击策略和评估方案

确定攻击策略是对供应链网络进行抗毁性分析的第一步，本文主要根据Albert提出的两种攻击策略进行分析：①随机攻击，在这种攻击之下，网络中的某个或某些节点因为不可预测的原因如自然原因或突发事件退出目标网络，该过程显然为随即发生；②选择攻击，在这种攻击之下，网络中特定的具有重要地位的节点将面临更高概率的破坏，这可以理解为一种人为的破坏，是有计划的选择性行为。

本章提出一种新的攻击模式：设置一个恒定的攻击总强度DS，按照等差数列设定攻击次数n，每次攻击强度按照公式ds=DS/n确定攻击次数。当攻击强度大于网络中节点强度时，则该点退出供应链网络，并取消其与邻接矩阵的联系；当攻击强度小于网络中节点的强度时，属于去边攻击，即随机删除该节点的部分边或将边上的权值降低。每种策略采用随机攻击和选择攻击这两种攻击策略。

网络受攻击后，通常可以从两个方面来分析网络：一是网络性能下降程度；二是网络拓扑的连通性破坏程度。本章选用网络连通性和网络全局效率作为网络抗毁性的考察参数，来考察在不同的攻击策略下网络性能的下降程度和网络连通性的变化。下面是对本章连通性和网络效率定义的公式。

1.供应链网络连通性

供应链网络的连通性是指网络面对节点删除的抗毁性表现，下式计算得到：(www.xing528.com)

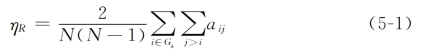
式中，aij为节点i到节点j连通参数，若节点i到j有路径，则aij=1，否则aij=0，GR是受攻击后的剩余网络的节点集合。网络的连通性反映的是网络被分隔的情况，即网络面对节点删除时网络性能的保持能力。

2.供应链网络全局效率

全局效率Eglobal为网络中两节点之间最短距离倒数之和的平均值［10］，可以按下式计算得到：

式中，Eglobal衡量信息并行传播时系统的效率，即全局效率。Eglobal∊［0，1］，当网络拓扑为完全图示时，Eglobal值最大，即Eglobal=1；当所有节点均为孤立节点时，Eglobal值最小，即Eglobal=0。

三、供应链网络抗毁性数值分析

本节采用HWSP模型模拟生成一个层次型复杂供应链网络，基于计算机软件模拟分析HWSP网络的抗毁性，其中n0=50（ns=25，nm=5，nr=20），m=3，S=15，N=1000。计算可得，网络中节点强度最大为4543，平均强度为40.582，因此，本章提出攻击总强度为10 000、攻击次数从1到20等差排列的攻击模式，如表5-2所示。

表5-2 HWSP模型攻击模式表

1.随机攻击

对HWSP模型生成的1000个点的层次型供应链网络进行随机攻击，攻击策略如表5-2中，固定总攻击强度为10 000，攻击次数分别为1-20的等差数列，每种攻击次数的攻击强度不同。随机选择网络中的节点进行攻击，若攻击强度大于被选节点的强度，则删除此节点，即该节点退出供应链网络；若攻击强度小于被选节点的强度，则随机删除与此节点相连的边，即该节点在供应链网络中的重要度降低。

2.选择攻击

对HWSP模型生成的1000个点的层次型供应链网络进行选择攻击，攻击策略如表5-2中，固定总攻击强度为10 000，攻击次数分别为1-20的等差数列，每种攻击次数的攻击强度不同。按照网络中度值越大的选择网络中的节点进行攻击，若攻击强度大于被选节点的强度，则删除此节点，即该节点退出供应链网络；若攻击强度小于被选节点的强度，则删除与此节点相连的强度越小的边，即该节点在供应链网络中的强度减弱。网络连通性变化如图5-4所示。

由图5-4可以看出，网络面对随机攻击和选择攻击时网络连通性的变化，选择攻击时的网络连通性下降速度快于随机攻击。计算可得，面对不同的攻击，随机攻击的网络连通性变化很小，当攻击次数n=16或20时，网络连通性反而上升，这个主要是因为随机攻击有可能会去掉网络中垃圾节点，使网络连通性上升；当攻击次数n=5、8、9时，网络连通性下降了4.55个百分点；网络平均下降0.2275个百分点。选择攻击对网络的连通性影响非常大，由图中菱形点曲线可以看出：对网络进行4次攻击和5次攻击的时候，线段斜率最大，网络连通性分别下降14.18个百分点和11.27个百分点，此时对网络的连通性影响最大；当网络遇到第6次攻击后，再对网络进行攻击，网络的连通性下降基本不变，呈现一条直线。因此，对网络进行4—5次攻击时，对网络的影响最大；总体而言，当总强度一定时，分多次对网络进行攻击对网络的效率影响更大，如图5-5所示：

图5-4 网络连通性变化图

图5-5显示的是网络效率的变化，网络面对选择攻击，网络效率的变化明显大于随机攻击。面对不同的攻击，随机攻击的网络效率变化不大，其中当n=3、4、6、16、19、20时，网络效率呈现上升趋势，其原因是随机攻击去掉了一些垃圾节点导致网络效率不减反增，整个网络平均下降0.64个百分点；选择攻击对网络的效率影响非常大，由图中菱形点曲线可以看出，网络效率下降速率是变缓的，对网络实施1次强度为10 000的攻击使网络效率下降最多，为29.56%；当n＞15时，网络的全局效率影响基本保持在0.1。因此，对网络中度值越大的节点进行攻击，其影响越大，总强度一定时，分多次对网络进行攻击对网络的连通性影响更大。

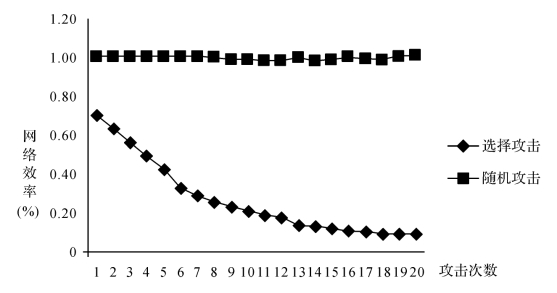
图5-5 网络效率变化图

综上可知，在选择删除的情况下，供应链网络是脆弱的，面对随机删除时，网络的抗毁性系数较高。上述供应链网络的连通性和网络效率可以看作在网络的拓扑结构上，物流、信息流和资金流的连通率和传递效率，衡量的是供应链网络结构的连通性。