HWSP模型数值模拟分析：一种新的视角

本节基于计算机软件编写程序，采用第三章第二节HWSP模型的演化机制，生成层次型加权供应链网络模型。本节首选构建一个由N=4000节点构成的层次型供应链加权网络，固定n0=50（ns=25，nm=5，nr=20），m=3，S=15，S1=350，S2=1500，即从包含50个全部有贸易往来的成员企业构成的供应链网络开始演化，假定其中原材料供应商有25个、生产商有5个、销售商有20个，每个节点的外包强度下限是350，上限是1500来执行网络的数值模拟。然后选取刻画复杂网络最重要特性的点度分布、点强度分布、集聚系数和平均最短路径等度量参数进行数值仿真模拟，从度分布、点权分布来对构造的层次型加权供应链网络模型的拓扑性质进行分析，最后分析各个参数在供应链网络中的实际意义。

一、度分布

按照上述供应链初始网络开始演化，可以选取不同的η值来执行网络的数值模拟。当η=0时，HWSP模型类似于LBBV模型，择优概率完全按照点强度选择；当η=1时，HWSP模型完全按照最短路径选择合作节点企业；当η=0.5时，HWSP模型折中选择连边节点。

如图3-4所示是HWSP模型的度分布图，对数坐标的横坐标为某一个度值k，纵坐标是度值为k的节点的概率P（k）。本文分别选取η=0，η=0.5，η=1进行模拟。由图3-4可以看出，HWSP模型的度分布是符合幂律分布的，即P（k）～k-γ。计算可得：当η=0时γ=1.2304，当η=0.5时γ=1.2520，当η=1时γ=1.2614，所以γ≈1.25。供应链中度值高的节点很好，这说明度值大的节点在网络中的概率小，大量高度值出现在低概率，即所谓的“长尾效应”，符合幂律分布规律。

图3-4 HWSP模型度分布图

二、点强度分布

供应链网络中点强度的定义是与之相连的边权总和，边权可以表示为网络中相连两企业节点间的交易量。供应链网络的点强度可以表示一个企业的供需能力，这是供应链里的重要统计指标和评价标准。

图3-5是HWSP模型的点强度分布图，对数坐标的横坐标是某一个点强度值ω，纵坐标是点强度值为ω的节点的概率P（ω）。本文分别选取η=0，η=0.5，η=1进行模拟。由图3-5可以看出，在双对数坐标下HWSP模型呈现良好的幂律尾分布，点强度strength很小的节点的概率很小，strength=12左右时的节点最多，而度值degree很大的节点的概率也很小，且权分布也像其他的现实复杂网络一样具有很重的尾部现象。

图3-5 HWSP模型点权分布图

三、度一点强度分布(www.xing528.com)

一般情况下，节点度值越大，其点强度越大。如图3-6所示的是HWSP模型的点强度与点度的变化关系，其中横坐标为某一个点度k，纵坐标是点强度值ω。本文分别选取η=0，η=0.5，η=1进行模拟。由图3-6可以看出，点强度越大的点，度值也越大，说明点强度和点度成正比增长，即ω∝k，符合现实情况。

图3-6 节点的点强度与点度的变化图

四、集聚系数

集聚系数C是复杂供应链网络中的一个重要衡量参数，集聚系数与点度的相关性如图3-7所示。图3-7显示的HWSP模型集聚系数与点度的相关性，横坐标为某一个点度k，纵坐标是该点的集聚系数C（k）X。本文分别选取η=0，η=0.5，η=1进行模拟。由图3-7可以看出，ETA=0时节点（“*”表示）比较聚集，因为新节点完全按照强度选择进入，容易使得网络节点聚集在一起，集聚系数比较大。图中大多数节点的集聚系数比较大，集聚系数C（k）随点度k的增加而逐渐下降，即点度大的节点集聚系数较小，点度小的节点互相之间联系紧密，可见，HWSP模型生成的网络是具有层次结构的网络。计算可得：当η=0时c=0.0104，当η=0.5时c=0.0110，当η=1时c=0.0121，所以c≈0.0112。该供应链网络集聚系数比较小，主要是因为供应链大多是线性的，这符合实际供应链网络的运作。

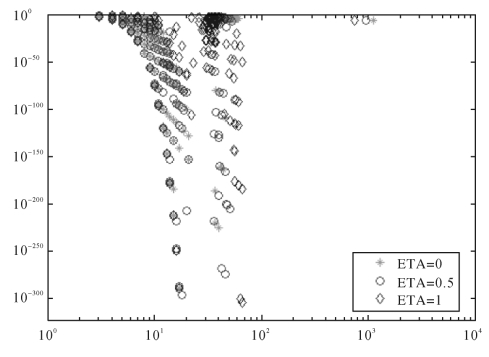
图3-7 聚类系数与点度的相关性图

五、平均最短路径

我们把网络中任意两个节点之间的最短路径求出来算出平均值，该平均值即为网络的平均最短路径。本节采用n0=50（ns=25，nm=5，nr=20），m=3，S=15，S1=350，S2=1500的演化机制，生成11个参数因子η均匀分布且不等的HWSP模型复杂供应链网络，计算这些网络的平均最短路径L如图3-8所示。

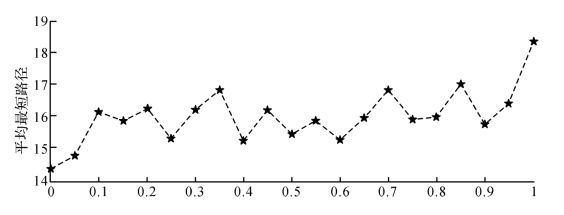
图3-8 HWSP模型的平均最短路径图

由图3-8可以看出，HWSP模型网络的平均最短路径大约在14～19之间，计算可得，平均L=16.0366，相比较其他复杂网络而言，其平均最短路径有点长，这主要是因为网络中没有进行跨层连接，而跨层连接对整个网络信息的有效传递可以起到非常重要的作用。