加权供应链网络的演化模型探析

供应链网络不能抽象为一般的无权复杂网络加以研究，因为无权网络只能给出供应链上主体之间的相互作用存在与否的定性描述，这种定性描述无法反映各主体相互合作最主要的信息。笔者认为供应链网络中各个结点成员受到自身“强度”“距离”及“偏好性”三个维度的影响，因此，供应链主体之间合作关系的重要性，即相互作用强度的大小，对供应链网络结构、功能演化有着至关重要的作用。而且供应链里的主体是分属性的，节点属性不同，连接概率不同，因此将供应链网络进行分层研究对供应链网络结构、功能演化也是至关重要的。综上所述，可以得出如下结论：将供应链网络抽象为层次型加权网络可以反映不同属性节点的更丰富的信息，而抽象为无权单顶点网络则不能很好地描绘供应链网络的特殊属性。

Yook等［6］在2001年提出了第一个加权的复杂网络演化模型，即YJBT模型。在该模型中，网络规模依据偏好性增长，根据偏好性的不同，生成的网络拓扑结构也不一样。该模型随机赋值给网络的边，演化机制和BA相似，但该模型的赋值不具有灵活性，不能随意改变。ZTZH（Zheng-Trimper-Zheng-Hui）模型是YJBT模型推广，是由Zheng等［7］提出的。他们在度和权的演化过程中加入了随机因素，但是该模型的不足之处也是边权一旦赋予，不再改变。

一、边权赋予方式

采用加权复杂网络研究层次型供应链网络的第一个问题就是边权的赋予方式问题，这个是把供应链网络抽象成加权复杂网络的必要工作，因为边权大小代表了供应链网络上主体之间相互作用的强度大小。研究者进一步将权重进行细分，原则上权重可以分为相似权（Similarity Weight）和相异权（Dissimilarity Weight）两种：相似权中，权值大小与两个节点之间的距离呈反方向变动趋势，与两点的关系紧密程度成正方向变动，即权值越大越紧密；而相异权则不同，权值大小与两个节点之间的距离成正方向变动，与两点的关系紧密程度呈反方向变动，即权值越小越紧密。在供应链网络概念中，权重并不是单纯的距离或单纯流量概念的定义，而是企业之间合作的紧密程度，相似权权值越大，两企业之间相互依赖的程度就越高，越需要相互合作；而相异权则恰恰相反，权值越大表示两个企业主体之间的关系距离越远，合作可能性越小。Zhang等［8］提出相似函数与相异函数表达式，见公式3-2和公式3-3。

相似权函数：

相异权函数：

相似权与相异权函数的关系如图3-1所示。

图3-1 相似权与相异权函数关系图

在复杂网络的研究领域，大多研究者采用给连接边加上权重和按照边的介数来赋权这两种方式对边权进行赋权，如表3-2所示：

表3-2 两种边权赋权方式表

在社会网络中，一般采用社会距离，即关系距离，来衡量两个主体（节点）之间关系的紧密程度，这种紧密程度反映在网络上就是两者之间的权重。［9］在本章的分析中，默认使用相似权来定义权重，并引入和使用合作次数和合作概率的概念（两个主体间没有连线即概率为0［10］）。合作次数或者合作概率大，说明两企业之间存在着比较高的相互依赖关系。对供应链网络赋权是一种通过调整节点之间关系来设置供应链网络性能的合理手段。复杂网络分析手段的应用，为改善网络结构和功能指明了新的方向。

二、层次型供应链网络上的统计量

在图论中，G=（V，E，W）是表示网络的经典方式。V，E，W分别为点，边，权，对应于供应链中的企业实体，企业间的边和企业间的合作关系。以一个矩阵W表示企业之间的合作关系，矩阵的行和列都为网络中企业的数量，wij表示企业i和企业j的合作关系，wij∊［0，∞］表示两个企业之间的合作关系从无开始不断加强。当每条边权重一样时，可以归一化为1，这时的网络为无权网络。

（1）节点企业的点度。

在复杂供应链网络中，描述企业主体和其他企业的联系的统计变量可以用点度ki，其计算公式为：

其中，aij用来表示两点之间的边存在与否。点度显示了与主体节点vi建立直接合作关系的伙伴数量，可以体现该节点企业在网络中的重要性。

（2）节点企业的点强度。

在复杂供应链网络中，描述企业主体综合能力和影响力的统计变量自然就是点强度si，其计算公式为：

其中，wij为vi和vj之间的交易关系强度，即其权重值。点强度不仅考虑了与主体节点vi建立直接合作关系的伙伴数量，还考虑了该主体和直接合作伙伴连接的权重，能综合地体现该节点企业的综合能力和重要性。

点强度分布P（S）主要是用来衡量企业主体具有点强度S的概率，它与度分布P（k）的作用类似，这两个分布反映了复杂供应链网络的基本统计信息。

（3）复杂供应链网络的集聚系数。

企业节点的集聚系数反映了该企业节点的一级近邻之间的集团特性。近邻节点之间合作次数越多，则合作关系就越密集，那么该节点企业的集聚系数就越高。供应链网络的集聚系数计算公式为：

（4）复杂供应链网络的最短路径。

在很多情况下，企业都会试图通过形成联盟来获取自己想要的东西，达到信息的共享。在当今战略联盟中，各个联盟主体可以通过从供应链网络中以最短的路径来获得自己想要的产品或者通过自己来获得，即自己生产各种外部资源。可想而知，第一种获取的方式更容易被企业所接受，因为其成本低，能够迅速获取。

在加权复杂网络研究领域，每条边关联的物理量对整个网络功能的影响是加权网络分析的主要考虑问题。对于位于D维欧式空间中的网络而言，两个节点之间的欧式空间距离就是连接两个节点间的长度，在无权复杂网络中，度量距离的方法就是把经过边数最少的路径定义为两个节点主体间的距离。而对于加权的复杂供应链网络而言，欧式空间的距离概念并不十分适用，由于不同的合作关系产生不同的权重，在度量距离时三角等式原则就失去了他的正确性。［11］

在供应链网络上，节点企业vi和vj之间的最短路径为i→k→j，通过两条权重分别为wik和wkj的边相连，则节点企业vi和vj之间的距离必须使用调和平均值，即lij=ωikωkj/（ωik+ωkj）来计算。同时，可以计算供应链网络上任意两点间的路径距离，进而可以得到任意两个企业节点间的最短距离及整个供应链网络的平均最短距离。

三、供应链网络演化生成的基本前提

本研究构建的供应链层次网络模型是有别于其他复杂网络模型的，该演化生成模式是建立在供应链实际运作的观察之上的，因此有以下六个前提条件。

前提一：供应链网络中的主体包括三种类型：原材料供应商、生产商、销售商，因此网络由这三种类型的节点构成。(www.xing528.com)

前提二：供应链网络具有层次结构性，同一类型的节点构成一层，总共三层。考虑到企业联盟、外包等关系，同层之间也有一定比例的连接，但主要是层与层之间的连接，另外跨层之间的连接暂时不予考虑。

前提三：供应链网络中允许新节点企业的自愿加入，但不考虑老节点企业的退出情况。

前提四：供应链网络中节点企业之间的关系以“联盟—合作”机制形成，除了考虑每个节点企业的局部利益外，还强调整个供应链网络的整体利益，旨在实现供应链网络的整体最优，实现“个体”与“整体”的和谐统一。

前提五：供应链网络中节点之间的连接采用点权有限的择优选择机制，即新的节点一般倾向于与那些具有较高强度的“大”节点相连接，即所谓的“马太效应”。但是研究发现，也存在有些节点会综合衡量点强度和路径，然后做出合适的选择。这符合现实中供应链网络的情况，一般企业都希望能够与实力较强的企业合作，但也会考虑到该企业的距离，因此，有时候最强的企业不一定会成为合作的对象。

前提六：供应链网络节点成员具有饱和度，节点企业会根据自身的节点容纳能力（超过一定的点强度）选择同层网络中的其他节点企业进行交互合作，简称“外包”，同时达到超容纳能力时不接受新节点的连接。

四、层次型复杂供应链网络模型算法描述

（1）综合考虑第三章第一节中介绍的复杂供应链网络演化的原理和机制，基于多主体建模方法，本文构造了基于点权和路径选择的层次型加权复杂供应链网络模型（HWSP模型，Hierarchical Weighting network based on Strength and Path），其生成的算法如下：

STEP1：初始状态t0时刻。

复杂供应链网络G（t0）开始是n0（n0=ns+nm+nr）个企业构成的层次型网络，共有三层（原材料供应商、生产商和销售商），其中ns个节点属于原材料供应商，nm个节点属于生产商，nr个节点属于销售商。其三种节点类型一定要满足一定比例ns∶nm∶nr，其中nm＜ns，nm＞nr。另外给它的每条边赋予权值w0=S×random［0，1］，设定有限点强度S1（si≤S1）、S2（S1＜S2），即当节点的点强度超过S1时，接纳新节点连接的同时外包给同层的其他节点，当节点的点强度超过S2时，不接纳新节点连接。其流程如图3-2所示。

图3-2 HWSP模型算法流程图

STEP2：三类节点的增长。

每间隔t时间添加一个新的节点n，并连接到m个已经存在的同类型节点上，且m≤nx（其中x为s、m或r），因此每次增加m条边。新增节点的类型按照概率来选择，概率属于原材料供应商节点、生产商节点和销售商节点的概率分别是ns/n0、nm/n0和nr/n0。根据新增节点的类型，其连接机制如下：

第一，n为原材料供应商：新节点n选择生产商nm类节点中的m（m＜nm）个节点进行连接，加入m条边，每条边的权重为wk=S×random［0，1］，新节点n连接到老节点i的概率满足择优选择规律：

其中，Πi为一个新节点与一个已经存在的节点i连接的概率；si为节点i的强度；ηi为利他偏好因子，ηi=0时新节点不偏向与i相连，ηi=1时新节点与i相连的概率最大；din为老节点i和新节点n之间的最短距离；j、k分别是生产商层中的节点的序号，从1开始。

第二，n为生产商：新节点n既要选择原材料供应商ns类节点中的m（m＜ns）个节点进行连接，加入m条边，又要选择销售商nr类节点中的m（m＜nr）个节点进行连接，加入m条边，每条边的权重为wk=S×random［0，1］，新节点n连接到老节点（属于原材料供应商层的节点）i的概率满足择优选择规律：

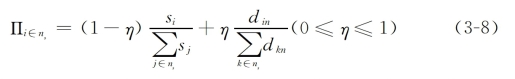
新节点n连接到老节点（属于销售商层的节点）i的概率满足择优选择规律：

第三，n为销售商：新节点n选择生产商nm类节点中的m（m＜nm）个节点进行连接，加入m条边，每条边的权重为wk=S×random［0，1］，新节点n连接到老节点i的概率满足择优选择规律：

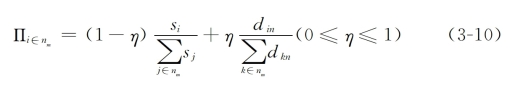
原材料供应商层和销售商层的连接规则一致，它们都是选择生产商层中的m个节点进行择优连接；中间的生产商层则略微复杂些，这一层的节点与上面的原材料供应商层及下面的销售商层都有连接，其连接择优规则是一样的，都是按照择优概率选择原材料供应商层和销售商层中的m个节点。

第四，检验择优规律公式3-7至3-10中被选取的m个节点的强度s，若节点i的强度si≥S，则节点i与新结点n相连，同时老节点i还与同层的其他点连接，连接满足如下择优选择规律：

STEP3：边权演化。

每次新加入的边<n，i>都赋予一个权值w0=S×random［0，1］，参照BBV模型的边权演化规则，本书认为新加入的边<n，i>只会局部地引发连接节点i与它的邻居节点j边的权重发生相应的改变，调整按照如下规则进行：

eij的边权wij发生改变，每次新引入一条边<i，j>，会给节点i带来额外的流量负担δi。δi为固定值，δi＜win时不会对相邻边权产生很大的影响；δi≈win时，新的边权win大致会被分配到其相邻的wij上；δi＞win时会对相邻边权产生很大的影响。

（2）上述模型的演化与所设的拓扑特征控制参数相关：

第一，复杂供应链网络演化过程中，新增加的企业的类型不一样，其连接增长的机制即企业选择合作伙伴（原材料供应商、生产商、销售商）的方式不同，参数ns∶nm∶nr的比例也不同，可形成各个行业的供应链网络的结构，如钢铁、电子、食品、纺织等行业；

第二，供应链网络生产的规模大小N，也直接关系到供应链网络的复杂性、层次性等宏观特性的体现并且间接影响到成员节点内部的微观属性值；

第三，择优连接规律中η值的不同，企业的综合能力、企业的偏好连接因素和企业间的距离占的偏重不一样，即它们在择优选择规律中的权重不一样，节点与节点之间的连接方式也会不一样；

第四，节点连接边的连接数量，即m值的改变会直接影响供应链网络增长过程的交易分布情况、新加入企业选择合作伙伴的方式，也间接影响到其他成员企业在整个供应链网络中的地位和重要程度。

通过这几个参数的调整，可获得不同结构的供应链网络的拓扑结构。