解析复杂网络中节点度值的概率分布特征

简单的系统会展现出复杂的行为，简单的规则自组织演化也可以形成复杂的系统，目前，用来刻画这种复杂性的重要的工具之一就是网络。网络就是由节点和边组成的，从广义上讲，现实生活中的各种网络中的个体可以看作成网络中的节点，个体之间的关系可以看作网络中的边。复杂网络可以用这种抽象的方式来描述现实的网络，小至朋友关系网络（如图2-1所示）等各种简单的网络，大至信息网络、社会网络。通过研究这些网络的拓扑结构和动力学特性，可以揭示网络的拓扑结构和由结构决定的功能、演化规律及动力学过程。

图2-1 朋友关系网络图

欧拉（Euler）开创了图论，第一次把网络的研究作为一门学科，而后Solomonoff和Rapoport及Erdos和Renyi引入了随机图论，带来了一个网络发展的重要阶段。而目前的研究热点主要是基于小世界网络和无标度网络。1967年，Stanley Milgram提出了著名的六度分离理论，他所做的小世界实验给出了这样的结论：一个人想要与地球上任意角落的人取得联系，中间只需要通过平均5个人的传递，地球上任意两个人之间的距离是6个人。1998年6月，Watts和Strogatz通过对小世界网络群体动力行为的研究，第一次指出了复杂网络所具有的小世界网络的特征，并提出著名的“WS小世界网络模型”，说明少量的随机连接会对网络的拓扑结构产生重大的影响。［1］1999年10月，Barabasi和Albert［2］通过对随机网络中标度的研究，进一步验证了复杂网络所具有的无标度网络的特征，并提出了著名的BA模型。此后，学术界对于复杂网络各方面的研究进入了一个新的时代：研究范围拓展；研究方向多元化；研究群体扩大化。在这样的研究环境下，复杂网络的研究甚至被称为网络新科学（New Science of Networks）。

复杂网络的研究发展过程如表2-1所示。

表2-1 复杂网络研究的简史表

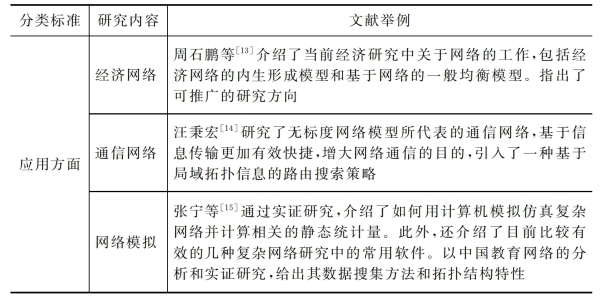
国内学者对于复杂网络的研究主要分为理论和应用两个方面。理论方面，演化网络、加权网络和动态网络是目前复杂网络研究的三个主要网络类型；另外还包括网络同步、网络控制和网络传播。应用方面，国内学者主要的研究涉及生物网络、广义合作网络、城市交通网络、制造网络、经济网络、通信网络及网络模拟。具体内容如表2-2所示。

表2-2 国内学者复杂网络研究现状表

续 表

目前，国内外关于复杂网络的研究可以简单地分为三个方面：复杂网络的静态统计性质；通过构建模型，进而研究复杂网络的统计性质和演化规律；预测网络系统的行为。

一、复杂网络的统计量

研究复杂网络及其相关问题，我们首先要从研究复杂网络的统计性质入手。目前学术界公认的用来测度复杂网络结构的统计特性有三个基本概念：平均路径长度（Average Path Length）；聚类系数（Clustering Coefficient）和度分布（Degree Distribution）。为了方便描述复杂网络的统计量，首先简单地定义一个复杂网络为G=（V，E），其中V和E分别代表网络中的所有节点和边。

1.平均路径长度

网络的平均路径长度也称为网络的特征路径长度。在复杂网络理论中，我们把网络中任意两个节点i和j之间的距离dij称为连接这两个节点最短路径上的长度，把网络上任意两个节点之间的距离的最大值称为网络的直径（Diameter），记为D，则D=maxdij，网络的平均路径长度L可以定义为任意两个节点之间的距离的平均值，其计算公式为：

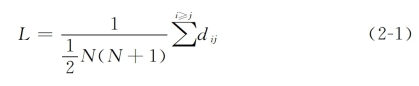
其中，N为网络中节点的个数。

2.聚类系数

聚类系数是描述网络中节点集聚特性的统计量。在一个网络中，有ki个邻居节点与节点i相连。所有ki个节点之间最多可能存在的边数为ki（ki-1）/2。定义ki个节点之间实际存在的边数Ei和总的可能的最多边数ki（ki-1）/2比例为网络中节点i的聚类系数Ci，即：

定义整个网络的平均聚类系数C为所有节点i的聚类系数Ci的平均值。

(www.xing528.com)

其中0≤C≤1。当C=0时表示所有节点都是单独存在的，即网络中没有任何节点互相连接；当C=1时网络变为全局耦合网络，即网络总是存在任意两个节点都是直接相连的。

3.度与度分布

网络中节点i的度ki是与该节点相连接的所有节点的数量。在复杂网络中，节点的度分布一般用分布函数P（k）来描述。P（k）表示在一个复杂网络中，任意一个节点的度值为k的概率。研究表明，规则网络的度服从Delta分布，随机网络的度近似服从泊松分布，然而许多现实中存在的网络的度分布与泊松分布具有明显的不同之处，他们大多数可以用幂律分布（Power Law Distribution），即P（k）∝k-γ来更好地描述，其中γ为幂律分布的幂指数。幂律分布的曲线比泊松分布的曲线下降要缓慢得多，更加符合现实网络的实际情况。

4.其他统计量

平均路径长度、聚类系数、度和度分布这三个统计量是复杂网络研究的基础，随着复杂网络研究的深入，现实网络中还有一些其他重要的统计性质也逐渐被研究者发现并重视起来。例如：用来描述网络节点的删除对网络连通性影响的网络弹性（Network Resilience）；用来描述网络中所有的最短路径中经过节点的数量比例的节点介数（Vertex Betweenness），以及类似的边介数（Edge Betweenness），介数反映了相应的节点或边在整个网络中的作用和影响力；描述不同网络结构之间的差异的度和聚集系数之间的相关性；以及描述加权网络中节点和边属性的点权和边权。

现实中的复杂网络主要分为社会网络，信息网络，技术网络和生物网络四大类，表2-3为各种现实网络的统计性质。其中N代表节点，M代表边总数，<k>为平均度数，L为平均路径长度，γ为幂指数，C为聚类系数，空格表示无可靠数据。“—”表示不符合幂律分布。

表2-3 各种实际网络的基本统计数据表

二、复杂网络模型

最早用来刻画复杂网络的两个模型是规则网络和随机网络。规则网络具有聚类系数大，平均路径长的特点，而随机网络恰好相反，它拥有比较小的聚类系数和短的平均路径。但是这两个网络的特殊性较强，现实中的网络的拓扑结构一般介于这两个网络之间，于是Watts和Strogatz为了更准确地描述现实网络的特征，提出了小世界网络，并构造了WS模型。具有算法如下：

（1）从规则网开始：假定有一个节点总数N，每个节点与它最近邻的K=2k个节点相连线的规则网络，其中N≥K≥1。

（2）随机化重连：以概率P随机重连网络中的每个边，即将边的一个端点保持不变，而另一个端点取为网络中随机选择的一个节点，并且排除自身到自身的连线和重复连线，即P=0。

当P=0时网络变成完全规则网络，而P=1时网络变为完全随机网络。随着P值的变化，网络逐渐从规则网络过渡到随机网络。其中当0＜P＜1时，网络具有比较大的聚类系数和较短的平均路径长度，此时的网络就是小世界网络。具体的演化过程如图2-2所示。

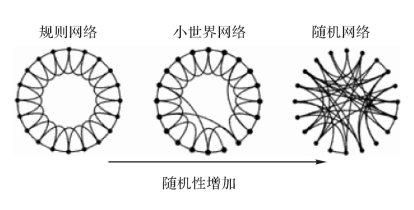
图2-2 规则网络、小世界网络、随机网络图

为了解决WS模型可能出现孤立集团的问题，Newman和Watts提出用NW小世界模型改进，NW模型把WS模型中的随机化重连规则改进为随机化加边，即先随机选取一对节点，然后在他们之间加边，加边时要删除自身到自身的连线和重复连线。

在前人研究的基础上，Barabasi和Albert提出了复杂网络具有无标度特性，并建立了著名的BA模型。BA模型是一个动态增长的演化模型，它描述了复杂网络的幂律特性。具体算法如下：

（1）初始，开始给定n0个节点；

（2）增长，在每个时间步重复增加一个新节点和m（m≤n0）条新连线；

（3）择优，新节点按照择优概率选择旧节点i与之连线，其中ki是旧节点i的度。

人们通过改变择优概率，又演化出了许多基于BA模型的新模型。

在对现实中复杂网络的研究过程中，我们有时必须要考虑网络中边的权重，即我们所谓的加权网络，目前研究的加权网络模型主要分为两大类：

（1）边权固定模型，即网络演化的过程中，为每一条边赋权，并且边的权重不随网络结构的演化而变化。具有代表性的是2001年Yook-Jeong-Barabas-Tu提出的YJBT模型，其演化过程与BA模型完全相同，并随机化为边赋权，边权值不随网络演化而变化。该模型的不足之处是边权赋值不可改变。其后出现的类似的改进模型如ZTZH模型等都具有类似的缺点。

（2）边权演化模型。边权固定的模型只是在无权网络的基础上给边赋权，并且权重不可演化，这些模型忽略了新节点或边加入网络可能引起的权值变化，不能说是严格意义上的加权网络。于是Barrat，Barthelemy，Vespignani等人在2004年提出了一个基于点强度驱动和边权逐渐加强机制建立的网络演化模型，即BBV模型。该模型生成的网络的度分布、点强度分布和边权分布都是幂律分布，并且幂指数介于2和3之间，具有无标度特性。但是BBV模型没有考虑真实网络演化中的一些因素的影响，比如节点吸引力，节点强度有限等。其他的模型还有Dorogovtsev Mendes提出的DM边权演化模型，该模型在边权演化过程中依赖权重大的边为其增加权重，并吸引新的连接。虽然该模型与BBV模型演化机制不同，但两个模型的统计量分布都是幂律分布。中科大小组提出了一个基于流驱动的加权网络模型。该模型在考虑了新节点加入的同时，还考虑了网络中时间演化导致的边权变化，以及节点退出导致的老节点之间产生新的连接而产生的影响。