跨区域行业的集聚分析

根据上文，我们得到444 个四位数代码的跨区域行业，下面，本文对444 个行业进行聚类分析，进而得到相应的产业集群的结果。该计算过程主要分为以下四个步骤。第一步，构建行业相关系数矩阵Mi £¬j ；第二步，根据行业的相关性矩阵Mi £¬j ，选择适当的参数；第三步，应用聚类分析的方法对行业进行聚类分析；第四步，根据不同的参数得到的多个产业集群，对每组产业集群结果进行评分，根据得分情况选取最适宜的参数，找到最优的产业集群结果。

首先，本文的相关性矩阵的计算为每个行业在各个地区的企业个数的相关系数，具体算法为地级市层面上两两行业的相关系数，计算公式如式（2）所示：

其中i 和j 分别表示行业i 和行业j，r 表示地区，因此根据以上公式，我们可以得到行业的相关系数矩阵。

在第二个步骤中对参数的适当选择，主要是对集群个数的选择。由于本文要对444 个行业进行聚类划分，因此本文考虑的集群个数的范围为2 到70 个。因为考虑到集群个数如果高于70 个，则每个集群内部的行业个数将过少，从而集群分类的意义不大，因此我们的集群个数选择区间定为2 到70 个。所以，在第三步中，我们将得到69 个可能的集群组成结果。为了判断集群的最适宜的个数，我们使用第四步对这69 个集群进行评分。现在对第四个步骤中评分标准进行相应的说明，判断集群划分的是否合理的重要标准为，集群内部的行业相关性要显著高于集群间行业的相关性，根据这一重要标准，并且参考 Delgado 等（2016）的评分体系，本文使用以下两个评分标准，分别如式（3）和式（4）所示：(www.xing528.com)

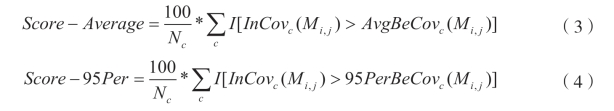
其中InCovc 为该集群内部的两两行业的相关性，即集群内行业相关性。BeCovc 为某一集群中的行业与另一个集群中的行业的相关性，即集群间相关性。Avg −BeCovc 为集群间相关性平均值，95PerBeCovc 为集群间相关性的95%跟位数。I（•）为判断函数，如果则记1，否则就记为0。同样的，则记1，否则就记为0。为集群个数。通过上述计算公式，我们得到两个评分，Score −Average 和Score−95Per，然后我们将这两个分值取平均数后得到69 个评分结果，具体评分如图24-1 所示。

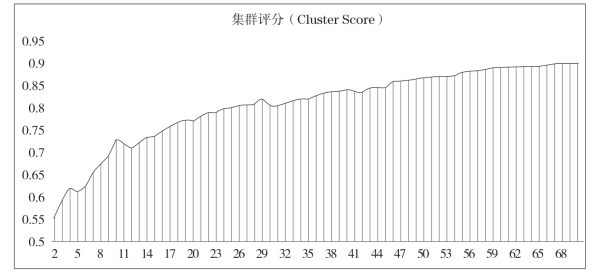
图23-1 69 个集群的评分趋势图

由图23-1 可以看出，随着集群个数的增大，集群评分逐渐增大，但是增大的趋势逐渐平缓，尤其是在集群个数在46 个之后，分值逐渐趋于平缓，因此本文认为，将集群个数定于46 个不失为一个适宜的选择。主要基于以下两个考虑，从69 个集群的评分趋势图来看，在少于46 个集群时，评分随着集群个数的增大而增大，并且趋势较为明显，在多于46 个集群时，评分的增大趋势逐渐趋于平缓；第二，考虑到如果集群个数过多，将导致集群内部行业数目逐渐减少，这会削弱对集群的行业研究的意义。因此，本文认为，最优的集群个数为46 个。附录一收录了该46 个集群的行业组成。