EOQ库存管理的优化方法

正如前文所述，为了保证正常的生产经营，所有的企业（包括JIT方式下的企业）都会保有一定量的库存。但是库存要付出代价，保持高库存是没有必要的。一方面需要存货，另一方面，持有存货既有成本又有风险，于是产生了库存控制上的一个重要问题：到底应该保有多少库存才算是合理的，这就产生了研究这种问题的方法，即订货批量为多少时最为经济。

经济订货批量（EOQ），即Economic Order Quantity，是固定订货批量模型的一种，可以用来确定企业一次订货（外购或自制）的数量。当企业按照经济订货批量来订货时，可实现订货成本和储存成本之和最小化。在库存管理中必须作出的基本决定之一就是对照发出重新补充库存的订单的成本平衡库存投资的成本。要回答的问题是，应该订多少货。正确的订货数量要使和发出订单的次数有关的成本与和所发订单的订货量有关的成本达到最好的平衡。当这两种成本恰当地平衡时，总成本最小。这时所得的订货量就称为经济批量或经济订货量（EOQ）。

7.3.1 确定型基本存储模型

确定型基本存储模型是假定需求不随时间变化的模型，有关参数如需求量、提前订货时间是已知确定的值，而且在相当长的一段时间内稳定不变。显然，这样经过数学抽象概括的条件在现实经济生活中是很难找到的，但我们认为，只要所考虑的参数波动不大，就可以近似认为是确定性的存储问题，我们先从简单的问题开始研究起，在后面的部分逐步加入变化的条件，研究模型的解，为库存的控制提供帮助和依据。

一、经济订货批量（EOQ）模型

1.经济订货批量的概念

经济订货批量（EOQ）模型又称整批间隔进货模型、EOQ存储模型。由于需求量和提前订货时间是确定已知的，因此只要确定每次订货的数量是多少或者进货间隔期为多长时间，就可以作出存储策略。由于存储策略是使用存储总费用最小的经济原则来确定订购批量，故称该订购批量为经济订购批量。

该模型适用于整批间隔进货、不允许缺货的存储问题，即某种物资单位时间的需求量为常数D，存储量以单位时间消耗数量D的速度逐渐下降，经过时间T后，存储量下降到零，此时开始订货并随即到货，库存量由零上升为最高库存量Q，然后开始下一个存储周期，形成多周期存储模型。

2.EOQ基本存储模型

（1）模型假设。

存储某种物资，不允许缺货，其存储参数如下所示：

T指存储周期或订货周期，单位为年、月或日；D指单位时间需求量，单位为件／年或件／月或件／日；Q指每次订购批量，单位为件或个；C1指存储单位物资单位时间的存储费，单位为元／（件·年）、元／（件·月）或元／（件·日）；C2指每次订货的订货费，单位为元；t指提前订货时间，此处假设为零，即订货后瞬间全部到货。

（2）建立模型。

存储量的变化如图7.2所示。

图7.2 整批间隔进货的EOQ模型存储量变化状态图

公式的推导过程如下：

一个存储周期内需用该种物资Q＝DT个，图7.2中斜线上的每一点表示在该时刻的库存水平，每一个存储周期存储量的变化形成一个直角三角形，一个存储周期的平均存储量为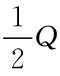，存储费用为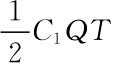在这个存储周期内存储总费用为 ，订货一次订货费为C2，因此，。

因为订购周期T是变量，所以只计算一个周期内的费用是没有意义的，需要计算单位时间的存储总费用CZ，即

将T＝Q／D代入上式，得

图7.3 订购批量与存储系统费用关系

显然，单位时间的订货费用随着订购批量的增大而减小，而单位时间的存储费用随着订购批量Q的增大而增大。如7.3所示。

由图7.3可以直观看出，在订货费用曲线和存储费用曲线相交处，订货费和存储费相等，存储总费用用曲线取得极小值。

利用微分求极值的方法，由式（7－1）可得

即得到经济订货批量

因为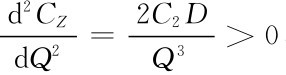，故当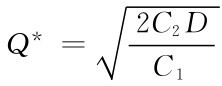时，CZ取得极小值。

式（7－2）被称为经济订购批量公式，又称为威尔逊公式。

由式（7－2）及Q＊＝T＊D，可得经济订货间隔期

将Q＊值代入式（7－1），得到按经济订货批量进货时，存储系统的最小存储费用为。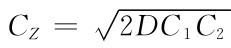

【例7－1】 某车间需要某种元件，不允许缺货，按生产计划均衡生产，月需用量D＝200件，每订购一次的订货费C2＝6元，该元件可在市场上立即购得，提前订货时间为零，已知其存储费C1＝0.8元／（件·年），问应如何组织进货？

解：按式（7－2），有

经济订购周期为

如以D表示某种物资的年需要量，V表示该物资的单价，C2为一次订货费，r表示存储费率（存储每元物资一年所需的存储费用），则得到经济订购批量的另外一种常用形式，可表示为

二、分批均匀进货的EOQ模型

由于这种模型最早用于确定生产批量，故亦称Production Lot Size（PLS）模型。在生产活动中，产品的生产时间是不容忽视的，即生产批量Q按一定的生产速度P，需要一定时间tp才能完成，也就是需方向供方订货，供方一边加工，一边向需方供货，直到合同批量全部交货为止。

1.模型假设

D、T、Q、C1、C2含义同前，不允许缺货。P表示单位时间的供货速度（生产量），且P＞D；tp表示生产批量Q的时间。在tp时间内，一边以P的速度供货（生产），一边以D的速度消耗，tp时间内的进货量满足一个订货周期T的需用量，即Q＝Ptp＝DT，所以tp＝DT／P。

2.建立模型

分批均匀进货的EOQ模型的存储量变化如图7.4所示。

图7.4 分批均匀进货的EOQ模型存储量变化状态图

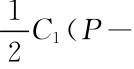
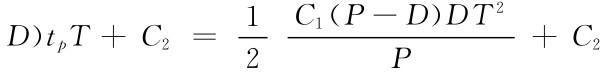生产批量（即订购批量）Q需时间tp，即tp也为进货延续时间；单位时间的产量P为进货速度。故在tp时间内库存的实际增长速度为P－D，最高库存量为（P－D）tp；平均存储量为；一个存储周期的存储总费用为 ，单位时间存储总费用为CZ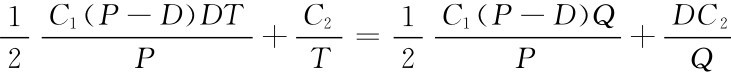＝令。利用微分求极值的方法， ，求得使单位时间存储总费用最低的经济订购批量为

经验证，知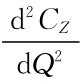＞0，故式（7－5）得到的Q＊使CZ取得极小值。

相应地，经济订购周期为

单位时间最小存储总费用为

与经典的EOQ模型相比，由于分批均匀进货，节省了存储费用，订购批量是整批进货的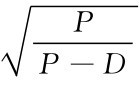倍，但单位时间存储总费用反而是原来的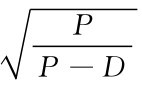倍。

【例7－2】 某厂每月需要某零件，该零件由本厂零件车间生产供应给装配车间。生产该零件的速度P＝8 000件／月，每组织一次生产因换工装夹具与调试生产线，需花费装配费（相当于订货费）C2＝500元。零件积压的存储费率为r＝0.08元／（元·年），该零件成本为V＝8元／件，问零件车间每月应如何组织该零件的生产及该厂全年为此需支付的存储费用是多少？

解：该零件单位时间的存储费用为C1＝r·V。由式（7－5）可得

可近似地安排每次生产3 000件，T＝3 000／3 000＝1（月），即每个月组织一次生产。如此安排，每年的存储总费用为

7.3.2 确定型扩展存储模型

在本节中，我们讨论的是加上了附加条件之后确定型存储模型的变化。

一、价格有折扣的EOQ模型

前面讨论的存储模型是比较简单的情况，都假定存储物资的单价是固定不变的，所以计算存储总费用时不考虑物资购货款。如果物资单价与订购数量有关，当订购批量达到一定数量时，单价可以有一定折扣，那么物资购买款就成为影响存储系统总费用的一个重要因素。这类存储模型称为价格有折扣的EOQ模型。

1.价格折扣的概念

在很多情况下，物资单价和订购批量是有关系的。许多厂家为了促销，会给不同的订购数量规定不同的优惠价格。当订购批量达到批发数量时，当一次订货数量可以凑足整车运输时，都可能给予一定的折扣，这类和订购数量大小有关的物资单价在建立存储模型时，称为价格折扣。

（1）第一种价格折扣形式。

一般来说，一次订购批量越大，单价越低。设单价有n级折扣，第一级折扣的最低一次订购批量最小，假定可以从零开始，单价最高，以后各级规定的最低一次订购批量逐级增加，而单价逐级降低，令Vj代表第j级的物资单价（Vj－1＞Vj）；Qj代表第j＋1级的最低一次订购批量（Qj＜Qj＋1），则当Qj－1≤Q≤Qj时，单价为Vj，购货款为QVj。按这种形式折扣所订购的物资，整批按一个统一的折后单价计算货款。

（2）第二种价格折扣形式。

这种折扣形式是在不同的数量范围内取得不同的单价，即单价有n级折扣。现规定Vj代表第j级的物资单价（Vj－1＞Vj）；Qj代表第j级的订购批量（Qj－1＜Qj）。当0＜Q＜Q1时，单价按V1计算；当Q1≤Q≤Q2时，Q1部分单价按V1计算，Q－Q1部分的单价按V2计算，其余Q－Q2部分按单价V3计算，以此类推。这种形式的价格折扣又称多种价格折扣。

2.第一种价格折扣的情况下的经济订购批量

下面从存储系统总费用最小的角度讨论较为常见的第一种价格折扣情况下的经济订购批量。

由于取得折扣价，所以购货款节省；同时，由于订购数量大，减少了订货次数，节省了订货费；但是存储费用增大。应权衡以上三个方面的费用，选择三者总和最小的订购批量为经济订购批量。

在不同的折扣价格Vj下，总货款与订货数量的关系如图7.5所示，而存储系统全年总费用（购货款、订货费、存储费）随订购批量Q而变化，如图7.6所示。

由图7.5可见，单价为Vj时Q的定义域为Qj－1≤Q＜Qj，定义域范围内的实线曲线段表示订购批量Q是实际可能发生的，定义域范围外的虚线曲线段表示订购批量是不可能发生的。年总费用随Vj不同而不同，它构成一组曲线。单价Vj越高（j值越小），曲线位置越高。寻找经济订购批量Q＊，即在定义域0＜Q＜＋∞范围内，找出年总费用曲线的最低点，其方法如下所述。

图7.5 订购批量—货款曲线图

图7.6 订购批量—总费用曲线

先求折扣价格Vj时的经济订购批量。用式（7－4）求理论经济订购批量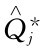，计算公式为

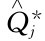如果处于实线段中，即，则即该折扣单价Vj时的经济订购批量；如处于虚线段中，则靠近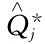的那个实线段端点即该折扣单价Vj时的经济订购批量。即

在求出不同折扣价格Vj时的经济订购批量后，其中使年存储总费用（包括购货款）最低的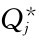为最终选定的经济订购批量Q＊。

【例7－3】 向批发商店订购某产品，批发商店规定，不同订货数量可以享受不同的折扣价格，如表7.1所示，年需要量为10 000件，该种货物不易腐败变质，不易过时，订货费为每次9元，年存储费率r＝0.08元／（元·年），求经济订购批量。

表7.1 订货数量与价格折扣、单价的关系

解：（1）按式（7－4）求出不同Vj时的理论经济订货批量。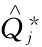

（2）按式（7－8）确定不同折扣价格Vj时的经济订货批量。

上述结果表明，按折扣价格18.00元计算得出的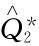2 值适用于250—999件的规定订货范围，而按折扣价格20.00元、16.00元计算得出的 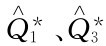均不在规定的订货范围内。所以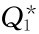取249件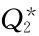，取353件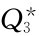，取1 000件。

（3）计算各Q＊j 时的年总费用。

（4）确定经济订货批量Q＊。(www.xing528.com)

比较各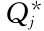年总费用，经济订货批量Q＊为1 000件。

如资金充裕，可将订购批量由249件调整到1 000件，这样包括购货款在内的全年存储系统总费用达到最小。

二、多种物资联合订购的EOQ模型

在实际采购物资时，一般是一次同时采购多种物资。这样，可以凑够一定批量，既便于装车又节省采购人力。例如，有A、B、C三种物资由同一厂家供应，存储周期分别为1个月、2个月、3个月，如将B、C两种物资的存储周期都压缩为1个月，则A、B、C三种物资由于有相同的存储周期就可以同时采购。这样做可以降低B、C两种物资的存储量，节省存储费，而且由于联合订购三种物资时，可以节省订货费用。下面就讨论多种物资联合订购的EOQ模型。

1.模型假设

联合订购集中物资，没有价格折扣；Di表示第i种物资的单位时间需求量；Qi表示第i种物资的订购批量；C1i表示第i种物资单位时间内单位数量的存储费用；C2表示每次订货的订货费用；T表示n种物资的共同存储周期。

2.建立模型

本模型的关键在于n种物资综合考虑，以存储总费用最小为目标，确定共同的经济存储周期T＊，从而确定各种物资的经济订货批量。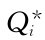

第i种物资单位时间的存储费用

n种物资单位时间的存储费总和为

单位时间的订货费为C2／T。

所以，单位时间的存储总费用为

上式对T求导，并令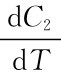＝0，得

所以，共同的经济存储（订购）周期为

第i种物资的经济订货批量为

这n种物资共同的最小存储总费用为

显然，当n＝1时，式（7－9）至式（7－11）与EOQ的基本公式相同。

【例7－4】 某厂使用A、B、C三种物资，年需要量分别为2 000、4 000、5 000个，单位时间存储费分别为0.1元／（个·年）、0.08元／（个·年）、0.15元／（个·年），每次采购的费用为150元，这三种物资可以同时采购，求共同的订购周期及各自的经济订购批量。

解：依照式（7－9），由于

D1C11＝2 000×0.1＝200（元／年）

D2C12＝4 000×0.08＝320（元／年）

D3C13＝5 000×0.15＝750（元／年）

所以

按照式（7－10）计算A、B、C三种物资各自的经济订购批量为

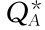＝2 000×0.486＝972（个）

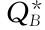＝4 000×0.486＝1 944（个）

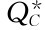＝5 000×0.486＝2 430（个）

按照式（7－11）计算联合订购的总费用为

而三种物资分别订购时对应的存储费用为

全年存储费用总和为

可见三种物资联合采购，全年可节省费用为

939.4－617＝322.4（元）

三、带资金（或库存容量）约束条件限制的存储模型

实际上，企业用于购货的资金是有总额限制的，假如各种物资按独立计算的订购批量进货，总库存占用资金就可能超过资金限额，而这在实际生产和管理上是不允许的。另外，企业的仓储能力是有限的，如按前述方法进货，各种物资的总储存量就有可能超过仓库的库容限制，给生产和管理带来不便并可能造成损失。这些存在于生产和管理上的实际限制，反映到存储模型中即为约束条件。这类模型称为带约束的存储模型。

带资金约束和库容约束的存储问题在建模思路和求解方法上是一致的。如果是单一品种物资，可求出其经济订购批量Q＊，如Q＊满足约束条件，则以Q＊订货；否则，将订购批量调整到约束条件允许的最大批量。如果是多种物资，先分别求出各自的订购批量，再检验各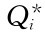值总和是否满足约束条件，如满足则按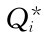订货；否则，就要寻找一种新的求解方法。在满足给定的约束条件的基础上，计算出使存储总费用最小的各种物资的经济订货批量。

带有约束的存储问题，要想求得其最优解，可用高等数学中的拉格朗日乘数法求有条件的极值，来解决这种带有约束的最优化问题，但这种算法的计算量较大。本节介绍一种近似的计算方法，本方法也适用于带约束的随机型存储问题。

1.模型假设

假设每种物资的提前订货时间和需求量确定已知，企业运用再订货点法控制库存（定量订购制）。共有n种物资，Di表示第i种物资单位时间的需求量；C1i表示第i种物资单位时间内单位数量的存储费；C2i表示第i种物资的一次订货费；Qi表示第i种物资的订购批量；Vi表示第i种物资的单价；r表示存储费率，即存储费用占库存平均额的百分比；L表示占用资金限制量。

2.建立模型

存储系统总费用为

约束条件（资金限制）为

按经济订货批量公式，可以解得各种物资的订购批量。当所有物资的平均库存占用资金超过设定的库存限额L时，就需要降低订购批量以减少平均库存，满足资金限额的要求。在EOQ基本公式中加入一个系数，使得重新求解出的各种货物的订购批量同水平的降低，以至于足以满足资金额度的限制。这样，基本的EOQ公式就修正为

式中，α是待定的常量。将式（7－13）代入式（7－12）得到求α的公式

求出α的值以后，将其代入式（7－13）就可以得到调整后的各种物资的订购批量Qi。

【例7－5】 假设企业有三种库存产品，相关数据如表7.2所示。管理人员对这些产品平均库存总额设定的上限为10 000元。年库存成本为平均库存额的30％，其他相关数据如下表所示，求三种库存产品的订购批量。

表7.2 库存产品的相关数据

解：按EOQ公式计算各产品单独订货时的订购批量。

总库存额＝0.5×（20×447.2＋10×912.87＋15×421.64）＝12 199（元）

总库存额超过了10 000元的限额。把相关数据代入式（7－13），得

将α＝0.146代入式（7－13）修正每一种产品的订购批量。

同理，求得Q2＝748.69（件），Q3＝345.81（件）。这样，平均库存额为10 004元，非常接近库存限额。

四、提价前的EOQ模型

如果已知某种物资将要提价，或者遇到以较低价格进货的机会，不应再按常规订货数量进货，而要从存储系统的购货款、订货费用、存储费用综合考虑（暂不考虑资金占用和贴现率问题），以总费用最小为前提，适当扩大订购批量。因此，这种提价前的EOQ模型又称遇低价时的EOQ模型。这种模型与前面有价格折扣的EOQ模型相比，最主要区别在于该模型虽然存在两种不同的价格，但对较低价并没有最低一次订购批量的限制，而且目前遇到的是一次较低价机会，今后将仍以较高价格进货。模型的关键也是求出最有利的经济订购批量Q＊。

1.模型假设

D、R、C2含义和前述一致；V1表示提价前的单价，V2表示未来提价后的单价，即V1＜V2，Q表示按提价前单价V1计价进货的订购批量。

2.建立模型

如按提价后单价V2计价，其经济订货批量为

按此批量订货的存储状态图如图7.7（a）所示。如按现行提价前的较低价V1进货，自然应扩大进货量，此时一次进货量为Q，图7.7（b）为按V1进货时的存储状态图。

图7.7 不同订购批量下存储量变化状态图

当订货批量增大为Q，按D的需求速度，可供Q／D时间使用。在这段时间内存储费用增加，但订货次数D／Q减少，使订货费用减少，由于单价较低，也可使货款减少。综合起来，在Q／D时间内有以下三个方面的费用变化。

（1）货款节省：Q（V2－V1）。

（2）存储费增加：按Q进货，平均存储量为Q，按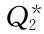进货，平均存储量为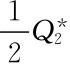，所以存储费增支为。

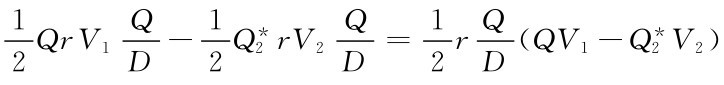（3）订货费用节省：如按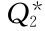批量订货，Q／D时间内共订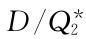次，所以订货费节省为。

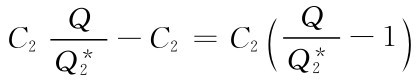共节省费用为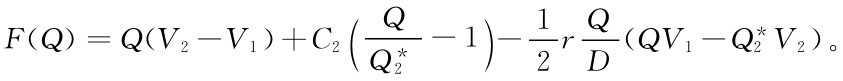

这样，使节省费用F（Q）取最大值时的Q＊值即为经济订购批量。

于是，令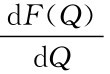＝0，即

因为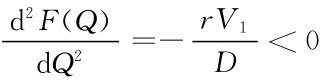，所以Q＊是使费用节省函数F（Q）取得最大值的点。

将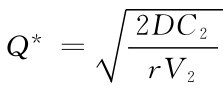代入上式简化后得到

【例7－6】 某工厂消耗某种零件9 000个，正常价格V2＝5元／个，现有可互用的同种零件价格V1＝3元／个。每次订货的订货费用C2＝25元，存储费率r＝0.25元／（元·年），问此时应购入多少零件。

解：按正常（高价）V2计价时，经济订购批量为

按所遇到的较低价格V1计价，使费用节省的经济订购批量，据式（7－14）计算为

可节省费用为

由本例可以看出，提价对经济订货批量有很大影响。当遇到较低价格时，在充分考虑资金的约束、仓库存储能力限制及物资本身是否会变质等条件下，可以扩大批量购置。在实际生产经营中，长期占用大笔资金，还应考虑贴现问题。