敏感性分析方法优化指南

1.单因素敏感性分析

这种方法是指每次只变动某一个不确定因素而假定其他的因素都不发生变化，分别计算其对确定性分析指标影响程度的敏感性。

【例题 9-5】设某项目基本方案的基本数据值见表 9-1，试对该项目进行敏感性分析（基准收益率ic=10%）。

表9-1　基本方案的基本数据估算表（单位：万元）

解：以净现值作为经济评价的分析指标，则预期净现值为

下面用净现值指标分别就期初投资额、营业收入和经营成本等三个不确定性因素作敏感性分析。

设投资额变动的百分比为x，投资额变动对方案净现值影响的计算公式为

设营业收入变动的百分比为y，产品价格变动对方案净现值影响的计算公式为

设经营成本变动的百分比为z，寿命期变动对方案净现值影响的计算公式为

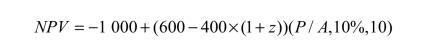
对期初投资、营业收入、经营成本在基准方案的基础上逐一变化±10%、±20% 取值，所对应的方案净现值变化结果如单因素敏感性分析表（见表9-2）和单因素敏感性分析图（见图9-5）所示。

表9-2　单因素敏感性分析表（单位：万元）

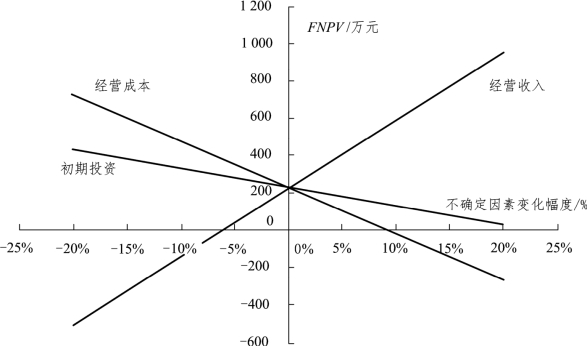
图9-5　单因素敏感性分析图(www.xing528.com)

可以看出，在同样的变动率下，营业收入的变动对方案净现值的影响最大，其次是经营成本的变动，期初投资额变动的影响最小。

根据上面的分析可知，对于本方案来说，营业收入是敏感因素，应对产品价格带来的营业收入进行更准确的测算。如果未来产品价格变化的可能性较大，则意味着这一方案的风险亦较大。

2.多因素敏感性分析

单因素敏感性分析方法适合于分析项目方案的最敏感因素，但它忽略了各个变动因素综合作用的可能性。无论是哪种类型的技术项目方案，各个不确定因素对项目方案经济效益的影响，都是相互交叉、综合发生的，而且各个因素的变化率及其发生的概率的是随机的。因此，研究和分析经济评价指标受多个因素同时变化的综合影响，研究多因素的敏感分析，更具有实用价值。

多因素敏感性分析要考虑可能发生的各个因素不同变动幅度的多种组合，计算起来要比单因素敏感性分析复杂得多。多因素敏感性分析一般是在单因素敏感性分析基础上进行，而且分析的基本原理和单因素敏感性分析大致相同，需要注意的是多因素敏感性分析中的假定同时变动的多个不确定性因素是相互独立的，且各因素发生变化的概率相同。另外，多因素敏感性分析计算比多因素敏感性分析计算复杂得多，常见的多因素敏感性分析有双因素敏感性分析和三因素敏感性分析。

常见的多因素敏感性分析有双因素敏感性分析和三因素敏感性分析，以下主要通过例9-6介绍双因素敏感性分析。

【例题9-6】设某出租经营的房地产，固定资产投资为170 000元，年租金收入为35 000元，年经营费用为 3 000 元，项目经济寿命为 10 年，固定资产残值为的 20 000元，基准收益率为 13%（现金流量图如图9-6所示），试就初始投资和年租金收入对该项目的净现值进行双因素的敏感性分析。

解：根据上述条件，设 x 表示初始投资变化的百分数，y 表示同时改变的年租金收入的百分数，则：

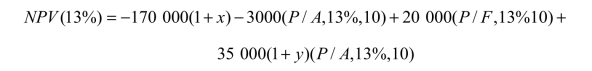
如果NPV（13%）≥0，则该投资方案收益率在13% 以上。

图9-6　本经营项目的现金流量图

即9 531.6－170 000x＋189 918.52y≥0，简化y≥－0.050 2＋0.895 2x

在以初始投资变化百分数x为横坐标和以年租金收入变化百分数y为纵坐标的平面图上，我们可知 y＝－0.050 2＋0.895 2x 与 x、y轴分别交于（5.62，0）和（0，－5.02）点作出y＝－0.050 2＋0.895 2x的一条直线，即NPV（13%）＝0的直线，则可以得到图9-7。

图9-7中由NPV（13%）＝0直线分割成两个区域。斜线以上的区域，NPV（13%）＞0，也就是该区域上的任何一对xy的变化率组合，该项目均能得到13% 以上的投资收益率，而且该组合离开 NPV（13%）＞0直线的距离越远，其抗风险的能力也越强；斜线以下的区域，NPV（13%）＜0，该区域中任何一个xy的变化率组合均会使该投资的收益率低于13%。从图9-7以看出，项目对投资的增加相对较为敏感。

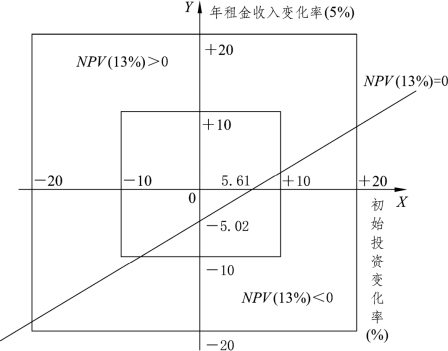
图9-7　双因素敏感性分析图

敏感性分析具有分析指标具体，能与项目方案经济评价指标紧密结合，分析方法容易掌握，便于分析，便于决策等优点，有助于找出影响项目方案经济效益的敏感因素及其影响程度，对于提高项目方案经济评价的可靠性具有重大意义。但是，敏感性分析没有考虑各种不确定因素在未来发生变动的概率，这可能会影响分析结论的准确性。实际上，各种不确定因素在未来某一幅度变动的概率一般是不同的。可能有这样的情况，通过敏感性分析找出某一敏感因素未来发生不利变动的概率很小，因而实际上所带来的风险并不大，以至于可以忽略不计，而另一个不太敏感的因素未来发生不利变动的概率很大，实际上带来的风险比那个敏感因素更大。这种问题是敏感分析所无法解决的，必须借助概率分析方法。