资金时间价值是工程经济分析的基本原理，资金等值计算是这个原理的具体应用。在进行计算时要注意严格按照基本公式应用的条件进行套用，不能直接应用公式时，可以进行适当的变换，使其符合基本公式。在变换过程中，常常用到名义利率和实际利率。
1.计息期与支付期一致的计算
【例题3-9】某企业有一笔投资，打算从第 17—20年的年末收回1 000万元。若年利率i＝10%，则此投资的现值是多少？
解：现金流量图如图3-8所示：
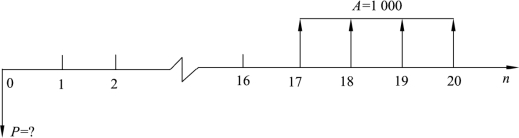
图3-8 现金流量图
方法一：根据一次支付现值公式计算：
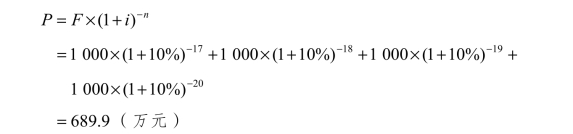
方法二：先根据等额支付现值公式将年金折现到第17年年初，再根据一次支付现值公式折现到0年的现值：
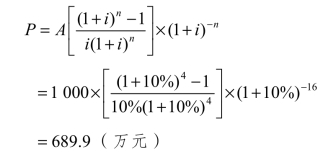
2.计息周期小于（或等于）资金收付周期时的等值计算
当计息周期小于（或等于）资金收付周期时，等值的计算方法有以下两种：
（1）按收付周期实际利率计算。
（2）按计息周期利率计算，即
F =P (F /P, r /m, mn)
P =F (P /F ,r /m, mn)
F =A( F /A, r /m, mn)
P =A( P /A, r /m, mn)
A =F (A /F ,r /m, mn)
A =P (A /P ,r /m, mn)
【例题3-10】某家庭购买商品房抵押贷款60万元，抵押贷款的期限为20年，按月等额偿还，年贷款利率为 6%，问月还款额为多少？如果该家庭30% 的收入可以用来支付抵押贷款月还款额，问该家庭须月收入多少，才能购买上述住宅？
解：
月贷款利率i=6%/12 =0.5%，计息周期数n＝20×12＝120（月），则月还款额：(www.xing528.com)
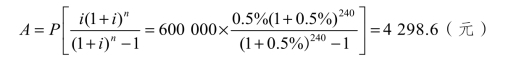
该家庭欲购买上述住宅，其月收入须为：4 298.6/0.30＝14 328.7（元）
3.计息周期大于收付周期
由于计息周期大于收付周期，计息周期间的收付常采用下列三种方法之一进行处理。
（1）不计息。在工程经济分析中，当计息期内收付不计息时，其支出计入期初，收益计入期末。
（2）单利计息。在计息期内的收付均按单利计息。
【例题3-11】付款情况如图3-9所示，年利率8%，半年计息一次，复利计息，计息期内的收付款利息按单利计算（单位：万元）。问：年末金额多少？
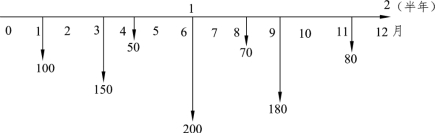
图3-9 现金流量图
解：计息期利率i=8%/2=4%，计息期内的收付款利息按单利计算：
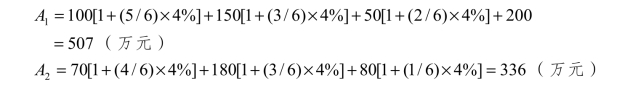
然后利用普通复利公式即可求出年末金额F为
F=507（F /P，4%，1）+336=863.28（万元）
（3）复利计息。
计息期长于支付期。以存款为例，通常规定存款满足计息期时才计利息，既在计息期间存入的款项在该期不计息，要到下一期才计利息。因此，在计息期间存入的款项，相当于在下一个计息期初的存入；在计息期提取的款项，相当于在前一个计息期末的支取。
【例题3-12】有一项财务活动的现金流量图如图3-10所示（箭头向上表示存款，箭头向下表示取款，单位：万元）。如果年利率为 12%，按季度计息，则这个现金流量年末的终值F是多少？
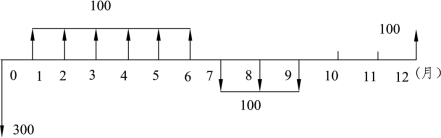
图3-10 财务活动现金流量图
解：由于计息期为每季度，且计息期内不计息，因此，将现金流量合并到每个季度的期末，合并整理后的现金流量图，如图3-11所示。
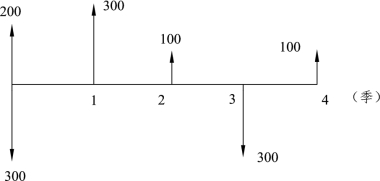
图3-11 财务活动整理后现金流量图
计息周期利率，即季度利率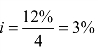
，所以本财务活动年末的终值为
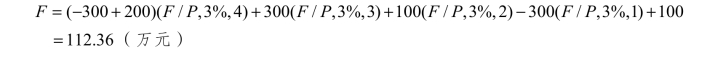
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
