考虑一个由制造商和零售商组成的两级供应链系统，假设系统内的各参数值分别为：p=30，w=10，ck=2，c=3，u=35，v=40，λ=1，ε和ξ均服从于[-15，15]的均匀分布。突发性需求前：批发价契约下，Kws=41.43；能力预约契约下，K*=47.78，ΠI（K）=847.22，τ=26%，r=1.48。以下对突发性需求下经能力预约契约协调的供应链参数变化情况进行讨论，几种情况下的供应链能力决策与利润比较如图6-1和图6-2所示。
图6-1 突发性需求前后供应链能力决策
①突发性需求信息对称且完全的情况下，Kcase1（ξ）=86.67+ξ，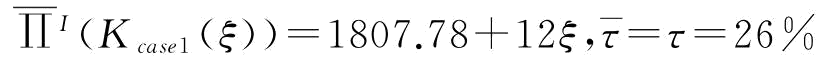
不变，
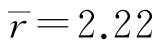，零售商需要向制造商支付η=35.39。②突发性需求信息对称但不完全的情况下，可计算出Kcase2=86.67，为常量与ξ无关，
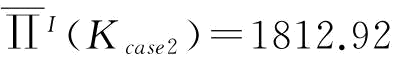，其他参数如
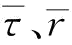和η都保持不变。③突发性需求信息不对称的情况下，可计算出Kcase3（ξ）=（2040+47ξ）/12，
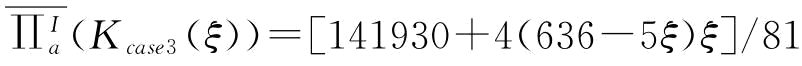，不对称信息下供应链要获得协调，原来的线性能力预约契约要修正为非线性能力预约契约后，供应链才能得到协调。由于P（ξ）是ξ的凹函数，供应商获得的能力预约费用要低于线性能力预约费用。
可发现：①突发性需求下，只要满足一定条件，扩张能力（Kcase1（ξ）、Kcase2、Kcase3（ξ）均大于K*）是有意义的，因为三种情况下的利润要比ΠI（K）大。②比较Kcase1（ξ）和Kcase2，当ξ=0时，式（6-7）和式（6-8）是等价的，即Kcase1（ξ）=Kcase2=86.67，相应的供应链利润均为1812.92。③比较Kcase1（ξ）和Kcase3（ξ），可以发现信息不对称下的供应链最优能力达不到信息对称且完全下的供应链最优能力，其利润同样如此；当前仅当ξ=15，即当制造商揭示出零售商最大信息时，供应链能力决策值达到最大，均为101.67，其对应的利润也达到最大，均为2167.78；图6-2中阴影部分为信息甄别所带来的信息租金对供应链造成的利润损失。④比较Kcase2和Kcase3（ξ），当满足式（6-14）即当ξ≥6.38时，Kcase3（ξ）≥Kcase2，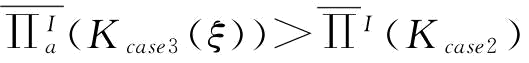
，也就是说当通过能力预约契约协调揭示出的信息足够大时，突发性需求信息不对称下的供应链能力决策要优于突发性需求信息对称但不完全下的供应链能力决策。
图6-2 突发性需求前后供应链利润
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
