我们认为突发性需求下的供应链能力应急是一个两期决策问题：第一期，制造商在市场需求D=u+ε的基础上建立能力；第二期，突发事件导致了突发性的市场需求v+ξ（假设突发性市场需求由v和ξ两部分组成，符号的界定由后面分别讨论），则新的市场需求为D+v+ξ=u+ε+v+ξ。需要指出的是，由于是突发性需求，所以我们假设由于受到突发事件的影响，市场需求变化的部分与原有的市场需求是独立的，即ξ是独立于ε的。
以下就供应链双方成员对突发性需求信息的了解的相关情况分别讨论：
（1）假设突发性需求信息对于供应链双方成员来说是对称的且是完全信息；即v、ξ是已知的，且为双方的共有信息。
（2）假设突发性需求信息对于供应链双方成员来说是对称的但是不完全信息；其中，v是已知的，ξ服从于均值为零、概率密度函数为g（.）、累计分布为G（.）的随机变量，双方对v和ξ的了解程度是一样的。
（3）假设突发性需求信息对于供应链双方成员来说是不对称的，其中v是已知的且为双方的共有信息，ξ是零售商的私有信息，而对于制造商来说是（2）中假设的随机变量，但制造商了解ξ的分布区间为ξ∈[a，b]。
突发性需求信息对称下，经过能力预约契约协调后的供应链、零售商和制造商的利润函数分别为：
其中，K为突发性需求下的供应链能力决策；K*为突发性需求前经能力预约协调后的供应链最优能力；λ＞0为打破原来生产计划增加能力部分K-K*所带来的额外单位能力成本。由于本文研究的是突发性需求下的能力决策，所以只考虑v+ξ＞0的情况。
1）突发性需求信息对称且完全
命题2：突发性需求信息对称且完全下，u、v、ξ是常数，ε是随机变量，供应链最优能力K为：
其中，
证明：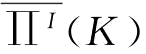
是严格凹函数，令
的一阶导数等于零，求得
所以，当
时，即当市场需求增大部分所带来的利润足够弥补调整能力所带来的成本时，增加能力到Kcase1才有意义；相反，当市场需求增大部分所带来的利润还不能弥补能力扩张所带来的成本时，能力扩张无意义，此时应保持原有的能力K*不变，得证。
命题3：突发性需求信息对称且完全下，通过调整参数r到
，可使得供应链重新得到协调，（其中
），制造商获得系数为τ的供应链利润加上常数项η，零售商获得系数为1-τ的供应链利润减去常数项η（其中η=（p-w）λK*/（p-c）），可参照命题1证明。
2）突发性需求信息对称且但不完全
命题4：突发性需求对称但不完全下，u、v是常数，ε、ξ是随机变量，供应链最优能力K为：
证明：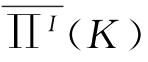
是严格凹函数，令
的一阶导数等于零，求得
当
，产能扩张到Kcase2，否则维持原有产能K*不变。至于如何协调该情况下的供应链能力，可参考命题3，协调中参数的变化是完全相同的。
通过比较命题1和命题3可以发现，无论突发性需求信息是确定还是不确定性的，只要供应链双方对市场需求的信息的认知是对称的，原有的能力预约协调还可以使用，也就是说能力预约协调具有一定的鲁棒性。特别指出的是，如果没有协调，制造商将单方面最大化自己的能力
为K≥K*时批发价契约下的供应链能力决策量，这个结果将在3.2中应用到。
3）突发性需求信息不对称
通过观察式（6-2）和式（6-3），可以发现零售商的利润是有关制造商提供的能力K单调递增的，而制造商则要为多余的单位能力付出成本ck。在双方的博弈中，当ξ为零售商的私有信息时，零售商有动力去夸大ξ的信息让制造商加大能力K，而制造商不相信零售商提供的有关ξ的信息，并根据对信息ξ的判断来调整能力K到Ka（Ka为不对称信息下经批发价契约协调的供应链能力决策），可求Ka=u+v+（F°G）-1（（w-c-ck-λ）/（w-c）），与式（6-9）一样，其结果中并不包含ξ。所以，无论在信息对称但不完全还是在信息不对称下，批发价契约下的供应链能力决策值一样。以下考虑用信息甄别博弈下的能力预约契约对供应链进行协调。
基于信息甄别博弈的能力预约契约下，供应链的决策顺序如下：①制造商提供一个契约组合{K（ξ），P（ξ）}（其中ξ∈[a，b]，P（ξ）是基于信息ξ的转移支付）；②给定契约组合，零售商选择
（其中，
是零售商给出的信息，不同于真实信息ξ；
是基于信息
的转移支付），制造商在收到
后建立能力
；③零售商在观察到市场的需求信息D后下订单；（4）制造商生产并发货
；（5）零售商在收到货物以单价p出售。(www.xing528.com)
突发性需求信息不对称下，经能力预约契约协调后的供应链、制造商和零售商的利润函数分别为：
制造商通过信息揭示原理（revelation principal）引导零售商给出真实信息ξ，使得自己的期望利润最大化，即有下式：
IC：
，对所有的
PC：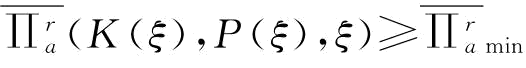
目标函数代表制造商期望利润；IC约束表示通过信息揭示使得零售商告诉真实信息所得要大于虚假信息所得；PC约束表示要保证零售商能获得一个最小利润
。
引理1：
证明：对式（6-11）求导，并令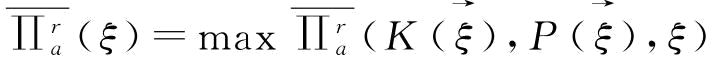
，则有
是ξ的递增函数，而ξ∈[a，b]，所以
当ξ=a时，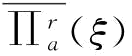
最小，得证。
由包络原理得：
对上式两边积分，并将
代入得：
所以，制造商的利润可以表示为：
根据积分中值定理，上式可表示为：
其中，（1-G（ξ））/g（ξ）（p-w）F（K（ξ）-u-v-ξ）为信息不对称下制造商为揭露零售商的信息而导致的利润损失。所以，制造商最大化利润的问题变为：
对上式进行一阶求导，则有：
即突发性需求信息不对称下的供应链最优能力K=Kcase3可由式（6-14）求出。
1）比较Kcase1（ξ）和Kcase3（ξ）
命题5：对于所有的ξ∈[a，b]，Kcase3（ξ）≤Kcase1（ξ）
证明：当零售商给出自己的真实信息ξ时，Kcase1（ξ）是式（6-4）或式（6-9）的最优能力，所以
；而Kcase3（ξ）是L（K（ξ），ξ）的最优能力，所以有：
-u-v-ξ）]≥0，由于F是增函数，所以Kcase3（ξ）≤Kcase1（ξ）成立。也就是说，突发性需求不对称下，如果零售商放大市场需求信息，那么通过能力预约下的能力Kcase3（ξ）依然达不到对称信息下的供应链最优能力Kcase1（ξ）。
2）比较Kcase2和Kcase3（ξ）
由于Kcase2的表达式里不包含ξ，同时式（6-14）也解不出Kcase3（ξ），无法建立Kcase2和Kcase3（ξ）的关系表达式，以下通过假定ε和ξ均服从[a，b]的均匀分布来计算并比较。
令Kcase3（ξ）-Kcase2≥0，可求得：当ξ≥b+（a-b）（c-p）/2（c-2p+w），Kcase3（ξ）≥Kcase2。所以，当揭示出的私有信息ξ足够大时，供应链信息共享程度提高了，信息不对称下的供应链比信息对称但不完全下的供应链愿意提供更多的能力。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
