从研究内容上来看,该部分与5.2部分的联系与区别是:5.2部分研究的是突发事件可能会造成供应链上游企业供应商生产运营系统中断,这种风险会传递给供应链下游企业制造商,制造商面临供应中断风险,而制造商通过设计一个补偿契约来引导供应商对恢复能力的合理投资;从风险的分类来看,第5章研究的是如何防范供应中断风险。而部分考虑的是在一个由多个供应商和一个制造商组成的装配式供应链中,当突发事件可能对不可靠的供应商造成冲击时,制造商为了防范供应中断风险可以事前采取相应的能力恢复措施并对供应商进行应急恢复援助;而供应链中其他的供应商为了防范制造商因订单取消所带来的需求中断风险,可以要求制造商在提交订单时先预付定金。从风险的分类来看,本部分将供应中断风险和需求中断风险纳入到一个框架进行研究,主要研究装配式供应链中制造商的应急恢复援助和供应商的订金决策。
中国期刊网中,搜索题为“订单取消”的学术文献,目前只有一篇,即范丽繁、陈旭(2012)[146]发表在《管理学报》上的论文“顾客可能取消订单的MTO企业订单定价策略”,该文研究了顾客下订单后可能取消订单的按订单生产型(Make To Order,MTO)企业如何定价以使得目标最大化。实际上,有关订单取消的文章可以参照Qi et al,作者研究了下游企业面临的市场需求面临突增或锐减下的供应链协调问题,其中,市场锐减下,上游企业面临订单被大幅取消的风险,作者研究了如何通过设计契约来协调供应链。于辉等、Chen and Xiao在同样的背景下研究其他的供应链契约协调问题。突发事件造成需求波动或中断下,现有的文献考虑的是:突发事件造成需求突变下,企业之间通过特定的契约如批发价契约、收益共享契约等来协调供应链。然而,在实际的供应链运营中,处于弱势地位的上游企业(例如,以汽车行业为代表的装配式供应链中,供应商往往处于弱势地位,而制造商往往处于强势地位)很难通过调整批发价来转嫁风险(生产计划已经安排好或者零部件已生产出来,但是订单被取消),在不公平博弈中,弱势企业只有被动接受订单被取消的风险。所以,弱势企业在订单可能被取消的情况下,只能主动地去防御风险,例如在顾客下订单时,可以要求顾客先预付一部分订金,当然在实现的订单下,订金是可以归还的(Deductible)。目前,在供应链产能的建立或扩张上,相关文献研究了通过交付订金的方式来预约能力,目的是激励上游企业建立更多的能力,如Erkoc and Wu(2005)[147]、Jin and Wu(2007)[148]研究了能力预约契约下的高科技产品能力扩张与供应链协调问题,Serel(2007)[149]考虑了现货市场不确定下,制造商与供应商的多周期能力预约契约问题,研究发现:相比价格契约,能力预约契约可以增加供应商对能力的有效利用。上述研究假设供应链下游企业制造商是主导博弈方,将其支付给上游企业供应商的单位预约能力的价格或订金被当作是一个常数,即由供应链下游企业决定的。然而,在现实中,供应链上游企业供应商也有可能是主导博弈方,其为了防范订单被取消的风险而制定订金决策(即将订金视为决策变量)也是符合现实情况的。
供应商通过预付订金的方式来转嫁风险,对于下游企业制造商来说,如何管理好其他供应商不可靠风险或突发事件风险成为当务之急。目前,对供应商不可靠下装配式供应链的研究主要有两类:第一类是研究供应链的订货决策与协调。Gurnani et al(2000)[150]研究了供应商不可靠/随机产出下使得期望总成本最小化的供应链协同问题。Kelle et al(2009)[151]、Keren(2009)[152]分析了随机产出对供应商最优决策及制造商的订货优化与协调策略的影响。Güler and Bilgic(2009)[153]进一步分析和比较了随机产出下不同的供应链契约的优化,如零售价格契约、回购契约、回购收益共享组合契约和改进的回购收益共享组合契约。He and Zhang(2008)[154]研究了供应商随机产出大于和小于制造商订货量的两种情况下,风险不共享和风险共享对供应商和制造商的最优决策的影响。Gurnani and Gerchak(2007)[155]、马士华和李果(2010)[156]通过引入惩罚机制研究装配企业的零部件订货决策与供应链惩罚契约。第二类是研究供应链恢复及应急援助问题,即不可靠的供应商在遭受突发事件后,可以事先通过建立恢复能力来进行修复,这一类文献在前面已详细说明。
基准模型描述的是研究对象在稳态时的决策问题,即当供应链成员在稳定的商业运营环境下的最优决策,这是研究当突发事件导致商业运营环境不稳定时,供应链成员援助决策和订金决策的前提和基础。本章研究的基准模型是一个常见的二阶段装配式供应链模型:由两个零部件供应商Si(i=1,2)和一个装配制造商M组成,M向Si分别采购零部件并进行1∶1∶1(可以理解为一个零部件A和一个零部件B经过加工装配成一个产成品AB)装配作业制造一种季节性商品面向市场。该部分主要研究稳态下的制造商的最优订货决策,相关参数假定如下:
q:制造商M的订货量;
r:市场零售价;
wi:供应商i的批发价格;
gm:制造商M的单位商誉成本;
gsi:供应商Si的单位商誉成本;
v:制造商M单位剩余存货的残值;
d:制造商面对的市场需求,d是随机变量,其分布函数为F(.)。
相关参数假设下,我们可以得到稳态下制造商的期望利润函数为:
其中,Ε为随机变量的期望;v(q-d)+为制造商剩余存货的残值;gm(d-q)+为制造商的商誉成本。由于min{q,d}=q-(q-d)+=d-(d-q)+,式(5-7)经过进一步整理可得:
式(5-8)对q分别进行一阶求导和二阶求导,可得:
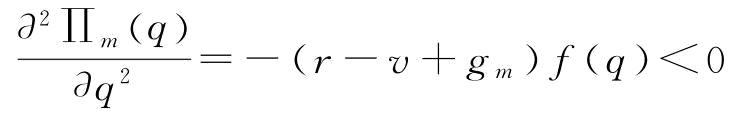 ,即Πm(q)是关于q的凹函数。令
,即Πm(q)是关于q的凹函数。令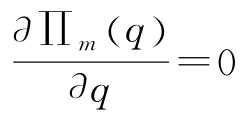 ,进而求得稳态下的制造商最优订货量或供应商的最优生产量为:
,进而求得稳态下的制造商最优订货量或供应商的最优生产量为: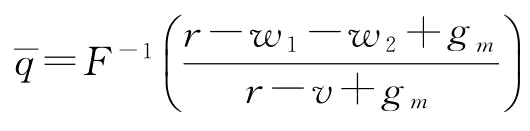
我们假设在装配供应链中,供应商S1处于自然灾害低发区,且供应商对生产工厂建筑物维护结构进行了加固并对生产设施进行了防火保护,从而突发事件下供应商S1是可靠的;而供应商S2处于自然灾害频发地区,且没有相应的安全措施,从而突发事件下供应商S2是不可靠的甚至生产运营中断,从而造成装配制造商M供应中断,进而造成供应商S1需求中断。当供应商S2突发事件发生后,制造商难以找到合适的替代供应源,由于存在商誉成本/订单拖欠成本,它向供应商S2提供应急援助。应急援助下,供应商S2可能不能完全恢复,其恢复的产量qe则取决于制造商的事前投入的恢复措施。同时,由于供应商S2不能完全恢复,制造商则可能会取消零部件供应商S1的部分订单,进而导致供应商S1面临极大的需求风险。事实上,供应商在接收到订单时可以要求制造商预先交付一部分订金以防范风险,供应商S1订金决策的依据则来源于制造商事前投入的援助措施e。所以,突发事件下,制造商恢复与供应商订金决策的顺序为:
(1)供应商S1根据订单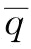 (稳态下制造商的订货量)进行生产,并宣布单位订货量的订金为w(假设0≤w≤w1,即单位订货量的订金不大于批发价,这与常理是符合的),需要制造商M提前支付订金
(稳态下制造商的订货量)进行生产,并宣布单位订货量的订金为w(假设0≤w≤w1,即单位订货量的订金不大于批发价,这与常理是符合的),需要制造商M提前支付订金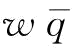 ;
;
(2)制造商M根据支付的订金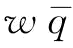 、供应商S2遭受突发事件的概率p以及自身的商誉成本gm制定援助恢复措施决策e,供应商S2的恢复产量为qe(因为稳态下,制造商M的最优订货量为
、供应商S2遭受突发事件的概率p以及自身的商誉成本gm制定援助恢复措施决策e,供应商S2的恢复产量为qe(因为稳态下,制造商M的最优订货量为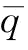 ;所以,
;所以,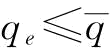 );
);
(3)制造商向供应商S1发出订单qe,供应商S1供货qe并归还制造商M未取消订单部分的订金。供应链的决策如图5-2所示。
图5-2 突发事件下供应链应急援助恢复与订金决策
突发事件可能造成供应商S2生产运营中断,制造商事前制定恢复措施并提供应急援助。制造商援助恢复的动力来源于两个方面:一方面是供应商S2供应中断带来的商誉损失;另一方面是突发事件下取消供应商S1订单所带来的订金损失。假设在应急援助恢复下,供应商S2的恢复产量qe与制造商的援助措施e的关系为qe=t(e),并满足一阶导数t′(e)大于零,二阶导数t″(e)小于零,即随着制造商援助措施的增加,供应商恢复产量呈递减的增加趋势,这与实际的供应链运营是吻合的。应急援助恢复下,制造商M的期望利润函数可以表示为:
其中, 。
。
式(5-9)中,x表示单位援助措施所投入的援助额;ex表示援助恢复措施e下所投入的援助额;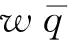 表示稳态下制造商支付的订金;p表示突发事件发生的概率。式(5-9)中,第一项表示支付的订金;第二项表示突发事件发生的情况下,制造商获得的利润与供应商S1归还的订金之和;第三项表示突发事件没有发生的情况下,制造商获得的利润与供应商S1归还的订金之和;第四项表示突发事件发生的情况下,制造商的商誉损失;第五项表示制造商提供给供应商S2援助恢复所投入的援助额。
表示稳态下制造商支付的订金;p表示突发事件发生的概率。式(5-9)中,第一项表示支付的订金;第二项表示突发事件发生的情况下,制造商获得的利润与供应商S1归还的订金之和;第三项表示突发事件没有发生的情况下,制造商获得的利润与供应商S1归还的订金之和;第四项表示突发事件发生的情况下,制造商的商誉损失;第五项表示制造商提供给供应商S2援助恢复所投入的援助额。
给定供应商S1的单位订货量订金w,以及供应商S2遭受突发事件的概率p,制造商可以优化自身的援助恢复决策,如命题4所示。
命题4:制造商最优援助恢复措施e*满足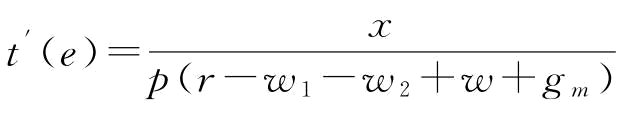
证明:式(5-9)分别对e进行一阶求导和二阶求导得:
其中,qe=t(e)。由于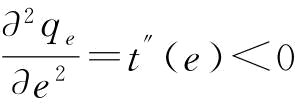 ,则
,则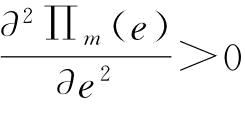 ,即Πm(e)是关于e的凹函数。令
,即Πm(e)是关于e的凹函数。令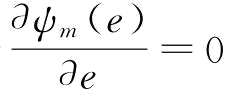 ,即可求得
,即可求得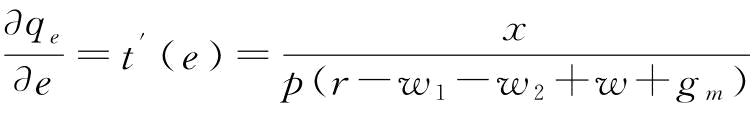 。证毕。
。证毕。
由于t′(e)>0,t″(e)<0,即t′(e)是关于e的减函数,即制造商的最优援助恢复措施e*是关于突发事件概率p、支付给供应商单位订单的订金w及制造商自身的单位商誉成本gm递增的,是关于制造商单位援助措施所花费的援助额x递减的。
命题1给出了突发事件下制造商最优援助恢复措施e*,由于订金w是供应商S1的决策变量,所以制造商投入的援助恢复措施则取决于p和w的大小,且e*是关于p和w的增函数。假设不存在订金即w=0时的援助恢复措施为en,则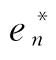 满足
满足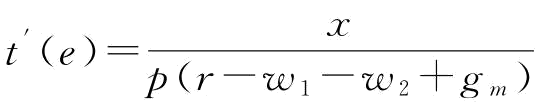 ,也就是说,即使供应商S1不制定订金决策,制造商也会投入援助恢复措施;而供应商S1之所以要制定订金决策,是希望制造商能投入更多的援助恢复措施,以降低自身订单被取消的风险。那么,供应商S1是否能无限增加订金,当订金满足什么条件时,制造商有意愿投入更多的援助恢复措施,从而使得供应商S2的产量恢复的更多?值得注意的是:
,也就是说,即使供应商S1不制定订金决策,制造商也会投入援助恢复措施;而供应商S1之所以要制定订金决策,是希望制造商能投入更多的援助恢复措施,以降低自身订单被取消的风险。那么,供应商S1是否能无限增加订金,当订金满足什么条件时,制造商有意愿投入更多的援助恢复措施,从而使得供应商S2的产量恢复的更多?值得注意的是:
(1)假设在不存在订金时,应急援助下的最优恢复产量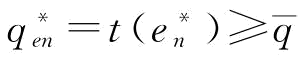 ,则供应商S1制定订金决策是没有意义的,因为此时供应商S2的最优恢复产量已经达到了稳态下的目标,供应商并不存在订单被取消的风险;
,则供应商S1制定订金决策是没有意义的,因为此时供应商S2的最优恢复产量已经达到了稳态下的目标,供应商并不存在订单被取消的风险;
(2)假设不存在订金时,应急援助下的最优恢复产量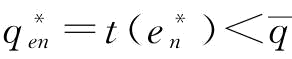 ,则该情况下供应商S1制定订金决策是有意义的,订金的存在是使得最优恢复产量
,则该情况下供应商S1制定订金决策是有意义的,订金的存在是使得最优恢复产量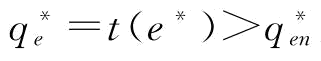 且
且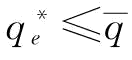 (即存在订金下的最优恢复产量要大于不存在订金下的最优恢复产量,但不超过稳态下制造商的最优订货量)。
(即存在订金下的最优恢复产量要大于不存在订金下的最优恢复产量,但不超过稳态下制造商的最优订货量)。
为了研究供应商S1的订金w满足的条件,我们将qe以显性函数的形式来表达。前面假设t′(e)>0,t″(e)<0,可以令qe=t(e)=aeb(其中,a是产量恢复的规模系数;b是产量恢复的弹性系数,0<b<1),进而可以得到命题5。
命题5:假设qe=t(e)=aeb(0<b<1),当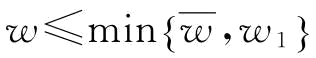 时,制造商M有意愿投入更多的援助恢复措施e,此时,
时,制造商M有意愿投入更多的援助恢复措施e,此时,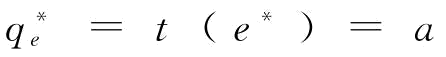
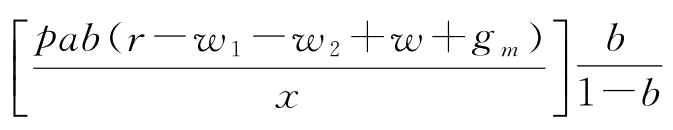 ;
;
其中,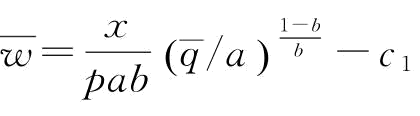 ,c1=r-w1-w2+gm,c2=r-v+gm,
,c1=r-w1-w2+gm,c2=r-v+gm, F-1(c1/c2)
F-1(c1/c2)
证明:由于qe=t(e)=aeb,则t′(e)=abeb-1;根据命题1的结论,abeb-1=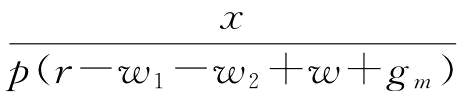 ,可以求解出
,可以求解出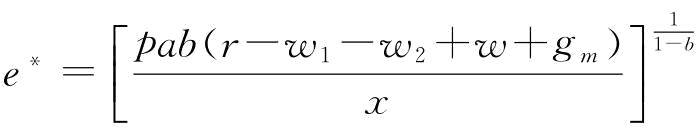 ,则供应商S2的最优恢复产量为
,则供应商S2的最优恢复产量为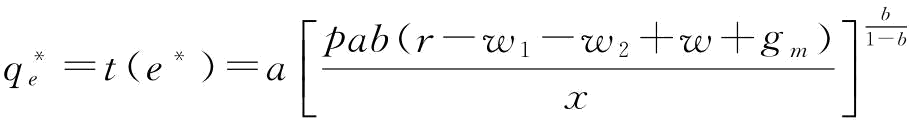 。由于
。由于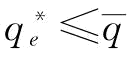 ,则有
,则有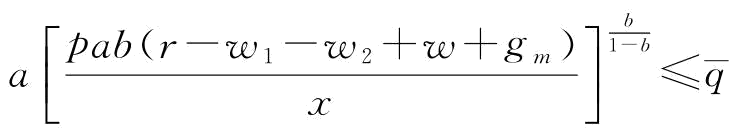 ;令c1=r-w1-w2+gm,c2=r-v+gm,求解上式得:
;令c1=r-w1-w2+gm,c2=r-v+gm,求解上式得: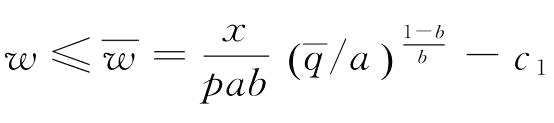 ,其中,
,其中,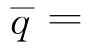 F-1(c1/c2)。
F-1(c1/c2)。
根据前面的假设:供应商S1收取的订金w不会大于批发价,即w<w1。所以,当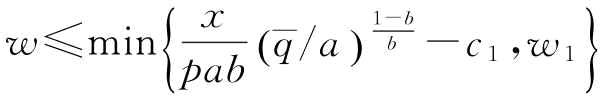 时,制造商M才有意愿投入更多的应急援助恢复措施e。证毕。
时,制造商M才有意愿投入更多的应急援助恢复措施e。证毕。
以上分析了当供应商S1的订金w满足什么条件时,制造商有意愿投入更多的援助恢复措施。那么,当存在订金下的供应商S2的恢复产量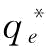 对突发事件概率p敏感性程度与不存在订金情况下的敏感性程度相比,哪个更高?供应商S2产量恢复的弹性系数b对这种敏感性程度又是如何影响的?相关结论如推论3所示。
对突发事件概率p敏感性程度与不存在订金情况下的敏感性程度相比,哪个更高?供应商S2产量恢复的弹性系数b对这种敏感性程度又是如何影响的?相关结论如推论3所示。
推论3:给定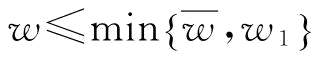 :
:
(1)若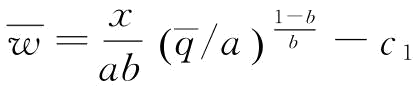 ,p∈[0,1]或
,p∈[0,1]或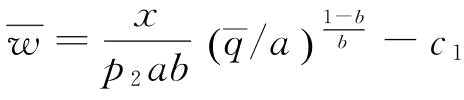 ,p∈[0,p2],
,p∈[0,p2],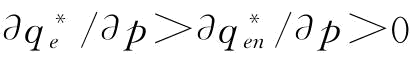 ;若
;若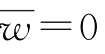 ,p∈(p2,1],
,p∈(p2,1],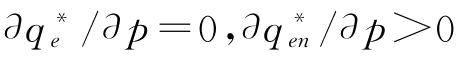 ;
;
(2)若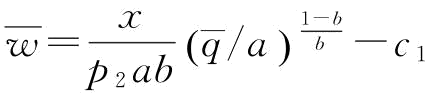 ,p∈(0,p2],
,p∈(0,p2],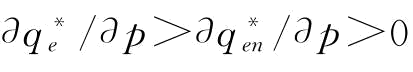 ;若w=0,p∈(p2,p1],
;若w=0,p∈(p2,p1],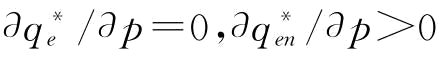 ;若p∈(p1,1],
;若p∈(p1,1], 。
。
其中,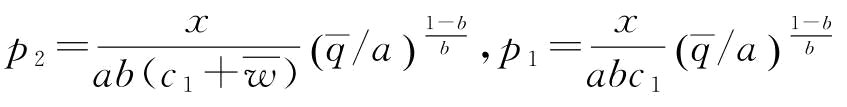 ;
;
(3)当b≥1/2,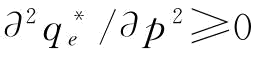 ;当b<1/2,
;当b<1/2,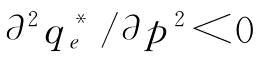 。
。
证明:当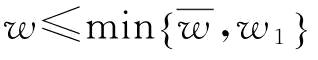 时,满足
时,满足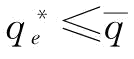 ,制造商有意愿投入更多的援助恢复措施。可以分为三种情况讨论,第一种情况是
,制造商有意愿投入更多的援助恢复措施。可以分为三种情况讨论,第一种情况是 恒小于
恒小于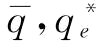 恒小于等于
恒小于等于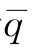 ,那么当p=1时,也满足
,那么当p=1时,也满足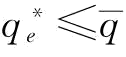 ;第二种情况是
;第二种情况是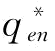 恒小于
恒小于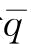 ,当p∈[0,1)时,满足
,当p∈[0,1)时,满足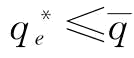 ;第一和第二种情况如图5-3所示;第三种情况是当p∈[0,1)时,
;第一和第二种情况如图5-3所示;第三种情况是当p∈[0,1)时,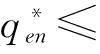
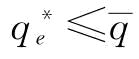 ,如图5-4所示。
,如图5-4所示。
(1)考虑第一和第二种情况:由命题5知,当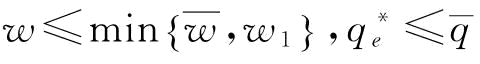 。若p=1时,
。若p=1时,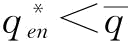 且
且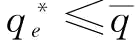 ;将p=1带入
;将p=1带入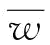 ,则有
,则有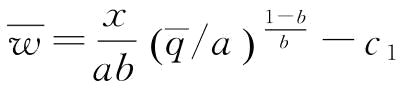 ;若p=
;若p=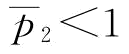 时(其中,
时(其中,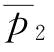 为
为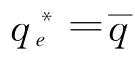 时所对应的p点)
时所对应的p点)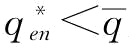 且
且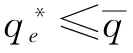 ,将
,将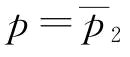 带入
带入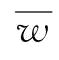 ,则有
,则有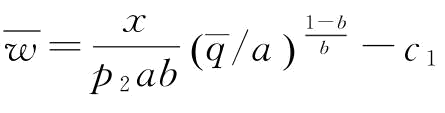 。由于
。由于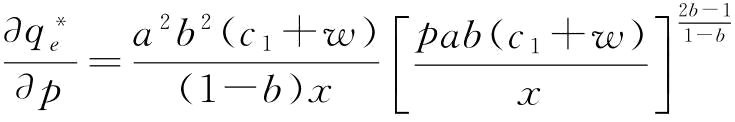 ,
,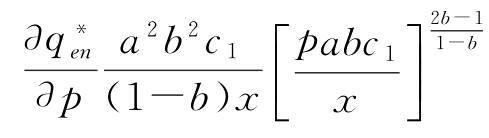 ,所以,若
,所以,若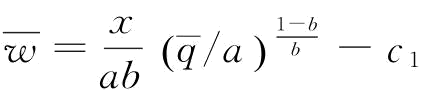 ,p∈[0,1]或
,p∈[0,1]或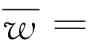
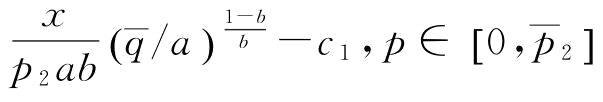 时,
时,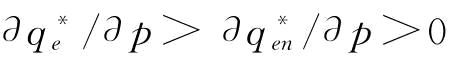 ;若
;若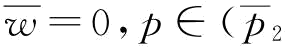 ,1],此时,
,1],此时,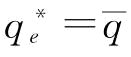 ,则
,则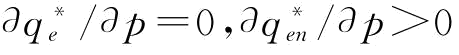 。
。
(2)考虑第三种情况:当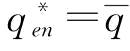 时,对应的p为
时,对应的p为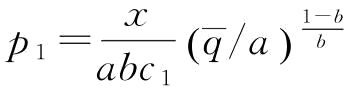 ;当
;当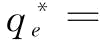
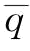 时,对应的p为
时,对应的p为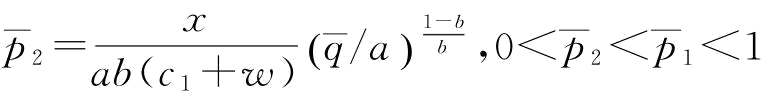 。当
。当 ,即当p∈
,即当p∈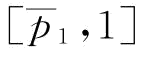 时,供应商S1制定订金决策没有意义,即w=0;当
时,供应商S1制定订金决策没有意义,即w=0;当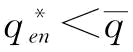 ,即当p∈(0,
,即当p∈(0,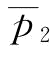 ]时,供应商S1制定订金决策有意义,此时
]时,供应商S1制定订金决策有意义,此时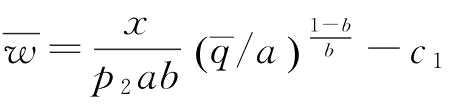 ;当p∈
;当p∈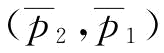 时,由于
时,由于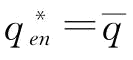 ,供应商S1制定订金决策也没有意义,即w=0。根据(1)的证明知:若
,供应商S1制定订金决策也没有意义,即w=0。根据(1)的证明知:若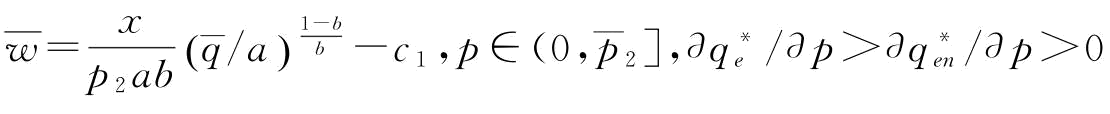 ;若w=0,
;若w=0,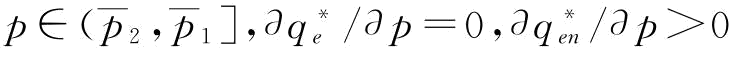 ;若
;若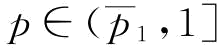 ,此时,
,此时,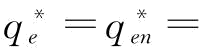
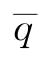 ,则
,则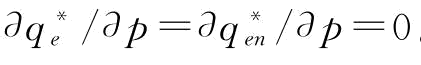 。
。
(3)由于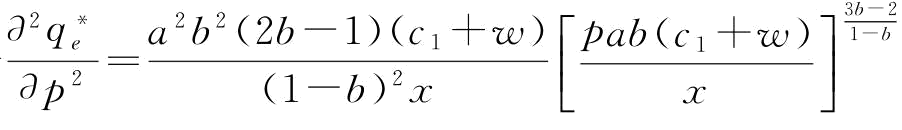 ,很明显,当
,很明显,当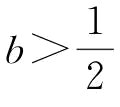 时,
时,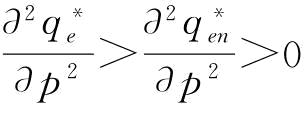 ;当
;当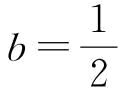 时,
时, ;当
;当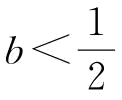 时,
时,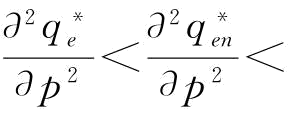 0。证毕。
0。证毕。
图5-3 情形1:突发事件概率对恢复产量的影响
图5-4 情形2:突发事件概率对恢复产量的影响
推论3给出了存在订金与不存在订金两种情况下的恢复产量对突发事件概率的敏感性,当突发事件概率在某一区间范围内时,突发事件概率越大,恢复产量越多,表明制造商对突发事件风险的态度是规避的;当突发事件概率超出某一区间范围时,随着突发事件概率的增加,恢复产量维持稳态下的最优产量不变,因为恢复产量不会超过稳态下的最优产量;由于订金的存在,当突发事件概率在某一区间范围内时,其恢复产量对突发事件概率的敏感性要高于不存在订金的情况;恢复产量对突发事件概率的敏感性要受到应急援助恢复弹性系数的影响,当弹性系数大于某一个值时,存在订金下的恢复产量对突发事件的敏感性比不存在订金下的敏感性增加的速度要快;相反,当恢复弹性系数小于某一个值时,存在订金下的恢复产量对突发事件概率的敏感性比不存在订金下的敏感性减缓的速度要快。以上说明了,恢复产量对突发事件概率的敏感性除了要受到订金的影响,还会受到制造商应急援助恢复的效率如恢复弹性系数的影响。
命题2和推论3分析了:制造商有意愿投入更多的应急援助恢复措施下,供应商S1的订金应该满足的条件;以及在给定订金所满足的条件,恢复产量对突发事件概率的敏感性。那么,在给定恢复产量下,供应商S1如何制定订金决策,使得自身的利润最大化?
由于商业信用的原因,在实际商业运营中订单可能被部分或全部取消,这取决于其下游企业的市场环境、供应链运营环境等。如前所述,在装配式供应链中:①装配制造商可能由于关键零部件的供应中断而取消其他供应商的订单;②由于存在商誉成本,制造商会帮助不可靠的供应商进行应急援助恢复。可靠供应商为防范订单取消带来的风险,要求制造商先预付订金,而其订金决策的依据则依赖于制造商预先所制定的援助恢复决策。
在制造商M提供给供应商S2援助恢复下,供应商S1的期望利润函数为:
式(5-10)中,第一项表示供应商S1收到的订金;第二项表示突发事件发生的情况下,供应商S1的收益减去归还的订金以及商誉成本;第二项表示突发事件没有发生的情况下,供应商S1的收益减去归还的订金。
式(5-10)进一步化简得到式(5-11):
对于供应商S1来说,不管供应链其他成员的运营状况如何,为了防范订单取消风险而制定订金决策是明智的。假定在不存在订金的情况下,供应商S1的期望利润是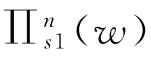 ,则由式(5-10)可知,
,则由式(5-10)可知,
式(5-10)减去式(5-12)得:
其,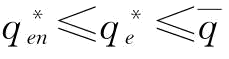 。
。
由于中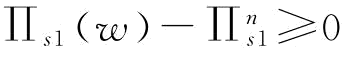 ,所以,供应商S1制定订金决策可以有效激励制造商投入更多的应急援助恢复措施,增加了供应商的恢复产量,降低了订单被取消的风险(当
,所以,供应商S1制定订金决策可以有效激励制造商投入更多的应急援助恢复措施,增加了供应商的恢复产量,降低了订单被取消的风险(当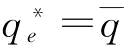 时,订单被取消的风险为零),进而增加了自身的期望利润,这与实际的供应链运营是吻合的。
时,订单被取消的风险为零),进而增加了自身的期望利润,这与实际的供应链运营是吻合的。
根据式(5-11),可以得到供应商S1的最优订金w*、供应商S2最优恢复产量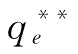 以及供应商S1的最优期望利润
以及供应商S1的最优期望利润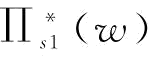 ,其中,
,其中,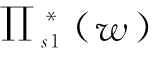 如式(5-14)所示
如式(5-14)所示
命题6:给定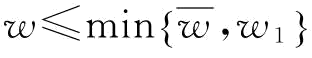 ,存在一个最优的订金
,存在一个最优的订金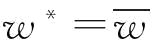 或w*=w1使得供应商S1的运营目标达到最优;当
或w*=w1使得供应商S1的运营目标达到最优;当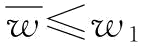 时,
时,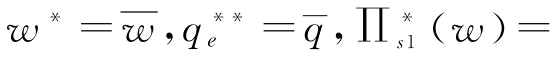
 ;当
;当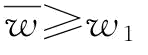 时,w*=w1,
时,w*=w1,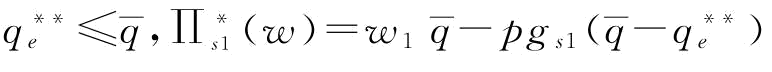 ;
;
其中,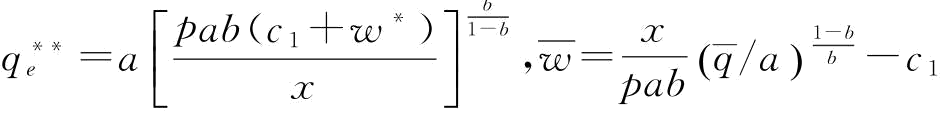
证明:式(5-11)对w一阶求导得:
其中,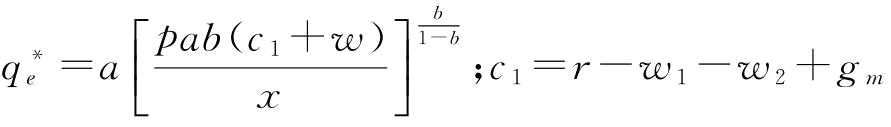 。
。
由于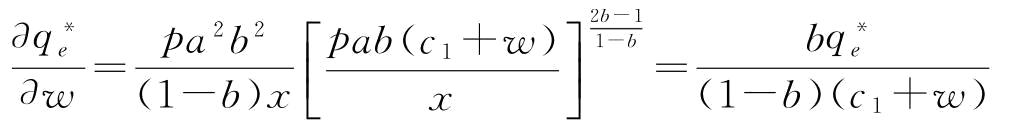
则有,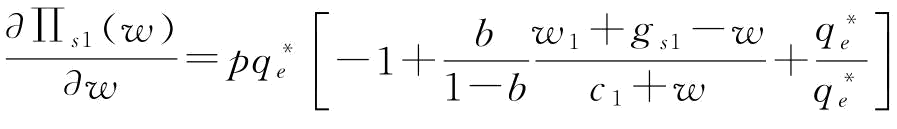
由于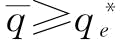 ,那么,
,那么,
以上说明了:w越大,Πs1(w)越大;而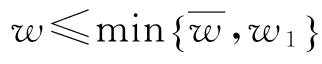 ;则w*取
;则w*取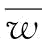 或w1;当且仅当
或w1;当且仅当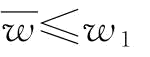 时,
时,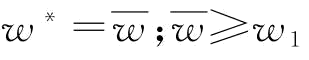 时,w*=w1。
时,w*=w1。
当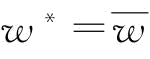 时,
时,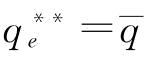 ,则
,则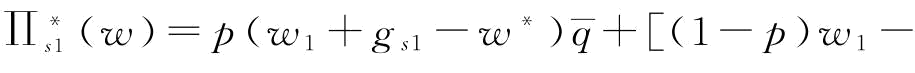
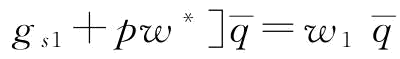 ;当w*=w1时,
;当w*=w1时, ,则
,则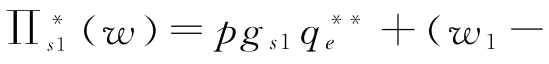
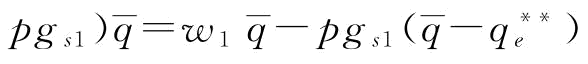 。
。
证毕。
命题6中可看出:突发事件下,存在一个最优的订金使得供应商S1的运营目标达到最优,最优订金的大小取决于供应商S2突发事件发生的概率以及制造商对供应商S2应急援助的效率如恢复弹性系数。
对于供应商S1来说,其制定订金决策是为了促使制造商增加应急援助措施,以提高供应商S2的恢复产量,进而增加自身的期望利润。供应商S1最优订金的制定则取决于突发事件发生的概率以及制造商对供应商S2应急援助的效率如恢复弹性系数;而最优订金又会影响到供应商S2的最优恢复产量,进而影响到供应商S1的最优期望利润。首先,给定恢复弹性系数,分析突发事件概率对最优订金、最优恢复产量以及供应商S1期望利润的影响。
1)突发事件概率对最优订金、最优恢复产量和可靠供应商期望利润的影响
推论4:保持b不变:(1)当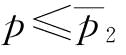 时,w*=w1,∂w*/∂p=0;
时,w*=w1,∂w*/∂p=0;
(2)当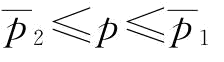 时,
时, ,∂w*/∂p<0;
,∂w*/∂p<0;
(3)当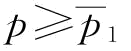 时,w*=0,∂w*/∂p=0;
时,w*=0,∂w*/∂p=0;
其中,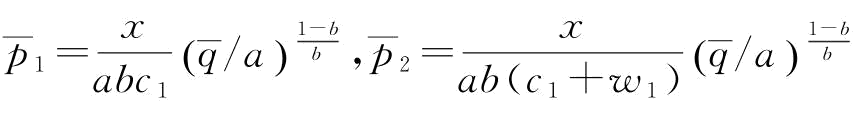
证明:由命题5知,当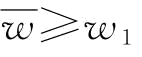 时,w*=w1,并将w*=w1带入推论3中的p2表达式中,则有:
时,w*=w1,并将w*=w1带入推论3中的p2表达式中,则有:
当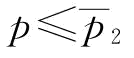 时,∂w*/∂p=0;当
时,∂w*/∂p=0;当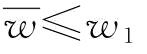 时,
时,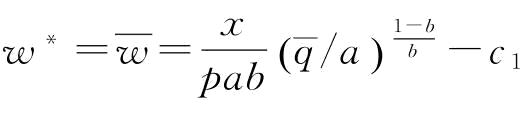 ,所以当
,所以当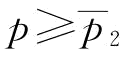 时,∂w*/∂p<0;特别地,当w*=0时,将w*=0带入推论1中的p1表达式中,则有
时,∂w*/∂p<0;特别地,当w*=0时,将w*=0带入推论1中的p1表达式中,则有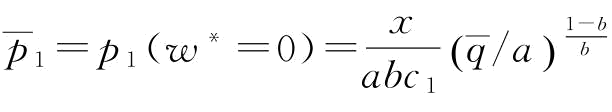 ,所以,当
,所以,当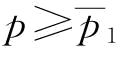 时,∂w*/∂p=0。证毕。
时,∂w*/∂p=0。证毕。
推论5:保持b不变:(1)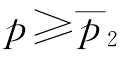 时,
时,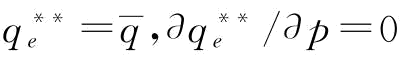 ;
;
(2)当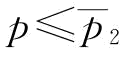 时,
时,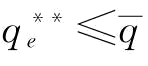 ,
,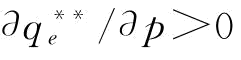 ;其中,
;其中,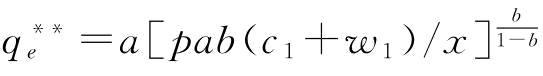
当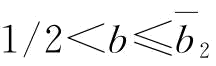 时,
时,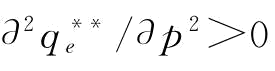 ;当b<1/2时,
;当b<1/2时,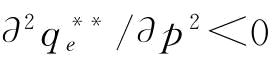
证明:由命题6和推论4可知:①当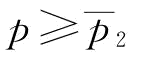 时,w*=0或
时,w*=0或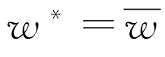 ,此时
,此时 ,则有
,则有 ;②当
;②当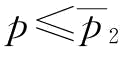 ,w*=w1,此时
,w*=w1,此时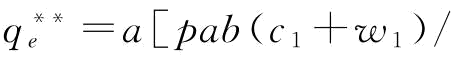
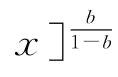 ,则有
,则有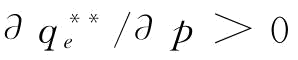 ;由推论3知,
;由推论3知,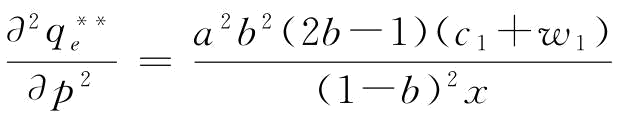
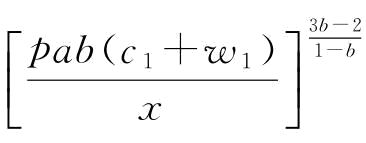 ,所以,当1/2<b<1时,
,所以,当1/2<b<1时,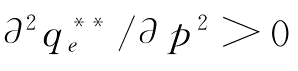 ;当b<1/2时,
;当b<1/2时,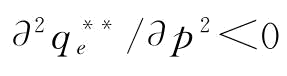 。证毕。
。证毕。
推论4和推论6中可看出,供应商S1的最优订金是突发事件概率的非递增函数,供应商S2的最优恢复产量是突发事件概率的非递减函数。如图5-5、图5-6、图5-7所示:
(1)若突发事件概率不大于某一个特定的值;当突发事件概率增大时,最优订金等于批发价保持不变,此时最优恢复产量没有达到稳态下的最优产量。
(2)若突发事件概率大于某个特定的值;当突发事件概率增大时,最优订金变小,但此时最优恢复产量达到了稳态下的最优产量。
以上可以解释为:突发事件概率本身就是制造商提供应急援助恢复的一个动力,当突发事件概率不大于某一个特定的值时,供应商S2的产量虽然在恢复,但恢复得较为缓慢,供应商S1为了促使制造商投入更多的援助措施,其制定的订金等于批发价(相当于一手交钱,一手交货);当突发事件概率大于某一个特定的值时,供应商S2的产量恢复良好;此时,供应商S1的最优订金对供应商S2的产量恢复的动力有所减弱,其最优订金在小于批发价的情形下就可以保证恢复产量达到稳态下的最优产量;而且,突发事件概率越大,最优订金会变得越小。特别地,当恢复弹性系数较大时,最优恢复产量增加的速度在加快。供应商S1最优订金决策下,突发事件概率对其最优期望利润的影响如推论6所示。
图5-5 突发事件概率对最优订金的影响
图5-6 当b<1/2突发事件概率对恢复产量的影响
图5-7 当b<1/2突发事件概率对恢复产量的影响
推论6:保持b不变:(1)当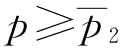 时,
时,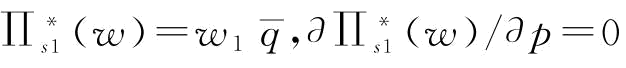 ;
;
(2)当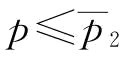 时,
时,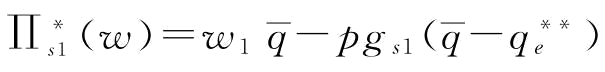 ;
;
当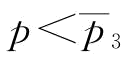 时,
时,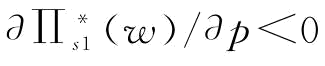 ;当
;当 时,
时,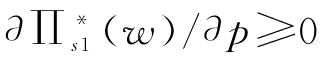 ;(https://www.xing528.com)
;(https://www.xing528.com)
其中,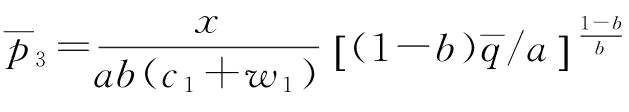
证明:由命题6和推论5知:
(1)当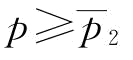 时,
时, ,并带入式(5-14),则有
,并带入式(5-14),则有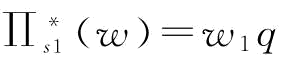 ,所以,
,所以,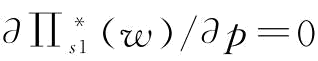 ;
;
(2)当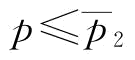 时,w*=w1;将w*带入式(5-14),则有
时,w*=w1;将w*带入式(5-14),则有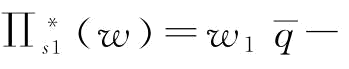
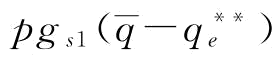 ,其中,
,其中,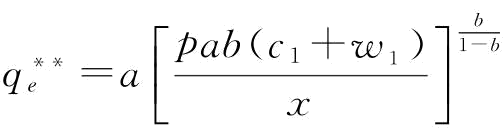 。
。
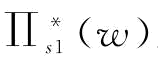 对p一阶求导得:
对p一阶求导得: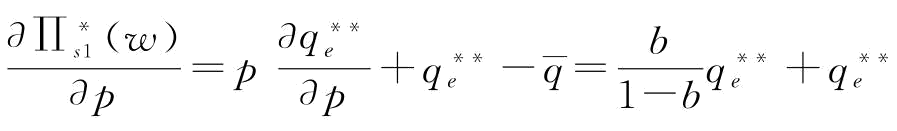
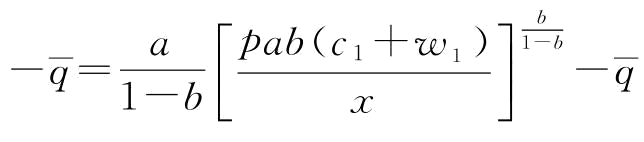 ;
;
若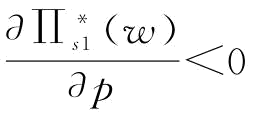 ,则有
,则有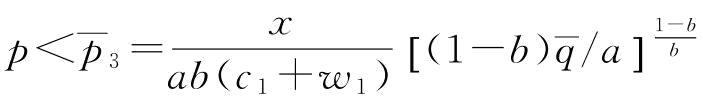 ;若
;若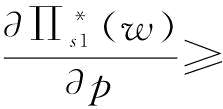 0,则有
0,则有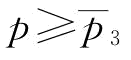 ;由推论4知,当w*=w1时,
;由推论4知,当w*=w1时,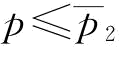 ,所以有
,所以有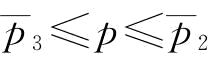 。证毕。
。证毕。
图5-8 突发事件概率对供应商S1最优期望利润的影响
突发事件概率对供应商S1最优期望利润的影响如图5-8所示。结合推论4、推论5和推论6,当突发事件概率到达某一个值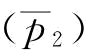 时,由于突发事件概率本身就是恢复的动力;那么,在订金小于批发价下,供应商S2的恢复产量达到稳态下的最优产量,所以供应商S1的最优利润达到稳态的最优利润。当突发概率小于等于某一个值(图5-8中的
时,由于突发事件概率本身就是恢复的动力;那么,在订金小于批发价下,供应商S2的恢复产量达到稳态下的最优产量,所以供应商S1的最优利润达到稳态的最优利润。当突发概率小于等于某一个值(图5-8中的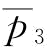 点),随着突发事件概率的增加,最优利润越小;突发事件大于这个值时,最优利润增加,直至增加到稳态下的最优利润。可以解释为:当突发事件概率较小(小于
点),随着突发事件概率的增加,最优利润越小;突发事件大于这个值时,最优利润增加,直至增加到稳态下的最优利润。可以解释为:当突发事件概率较小(小于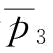 )时,即使单位订金等于单位批发价,但由于恢复产量较小,供应商S1收取的订金所获得的收益完全不能弥补订单被取消所带来的损失;当突发事件概率较大(大于
)时,即使单位订金等于单位批发价,但由于恢复产量较小,供应商S1收取的订金所获得的收益完全不能弥补订单被取消所带来的损失;当突发事件概率较大(大于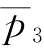 小于
小于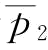 )时,单位订金等于单位批发价,由于恢复产量较大,供应商S1收取的订金所获得的收益能部分弥补订单被部分取消所带来的损失。
)时,单位订金等于单位批发价,由于恢复产量较大,供应商S1收取的订金所获得的收益能部分弥补订单被部分取消所带来的损失。
2)恢复弹性系数对最优订金、最优恢复产量和供应商S1期望利润的影响
推论7:保持p不变:(1)当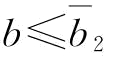 时,w*=w1,∂w*/∂b=0;
时,w*=w1,∂w*/∂b=0;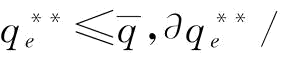
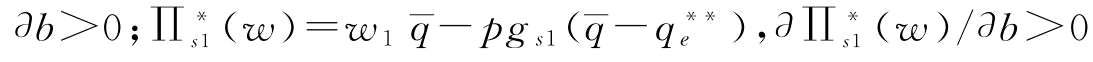 ;(2)当
;(2)当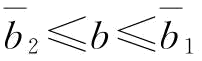 时,
时,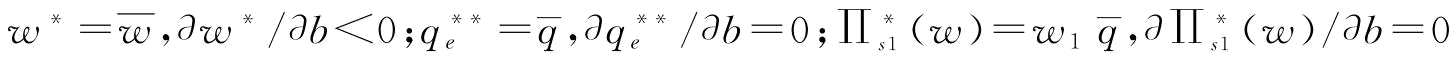
证明:令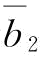 和
和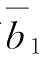 分别为
分别为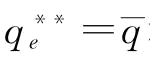 和
和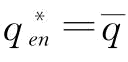 时b的解;
时b的解;
当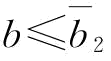 时,
时,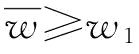 ,则w*=w1;
,则w*=w1;
当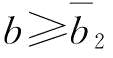 时,
时,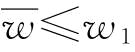 ,则
,则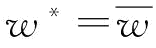 ;
;
特别地,当 时,w*=0。
时,w*=0。
根据命题6的结论:当w*=w1时,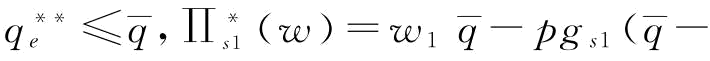
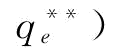 ;当
;当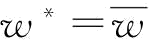 时,
时,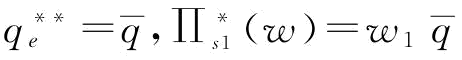 ;
;
w*、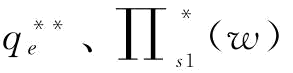 分别对b求一阶倒数,结论如推论7所示。
分别对b求一阶倒数,结论如推论7所示。
图5-9 恢复弹性系数对最优订金的影响
图5-10 恢复弹性系数对恢复产量的影响
图5-11 恢复弹性系数对最优期望利润的影响
推论7可看出,供应商S1的最优订金是恢复弹性系数的非递增函数,供应商S2的最优恢复产量和供应商S1的最优利润是恢复弹性系数的非递减函数。如图5-9、图5-10、图5-11所示,保持突发事件概率不变时:
(1)若恢复弹性系数不大于某一个特定的值,供应商S1为了防范应急恢复能力不足,其最优订金等于批发价保持不变,即相当于一手交钱,一手交货;此时,最优恢复产量没有达到稳态下的最优产量,最优利润也没有达到稳态下的最优利润。
(2)若恢复弹性系数大于某一个特定的值,供应商S1的最优订金对供应商S2的产量恢复的动力有所减弱,其最优订金在小于批发价的情形下就可以保证恢复产量达到稳态下的最优产量,最优利润也达到稳态下的最优利润;而且,恢复弹性系数越大,最优订金会变得越小。
可以进一步地解释为:当援助效率不足时,即使最优订金等于批发价,最优援助恢复产量也达不到稳态下的最优产量;当援助效率相对较强时,即使最优订金小于批发价,最优恢复产量也可以达到稳态下的最优产量,此时供应商S1的最优利润可以达到稳态下的最优值。
3)突发事件概率和恢复弹性系数的联合影响
以上分析了,最优订金、最优恢复产量和供应商S1最优利润分别对突发事件概率和恢复弹性系数的敏感性。那么,突发事件概率和恢复弹性系数对供应商S1最优决策的联合影响如何,如推论6所示。
推论8:(1)当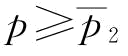 或
或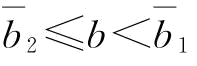 时,∂2w*/∂p∂b>0;
时,∂2w*/∂p∂b>0;
(2)当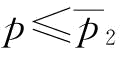 或
或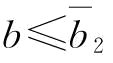 时,
时, ;
;
证明:
(1)当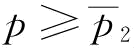 或
或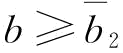 时,
时,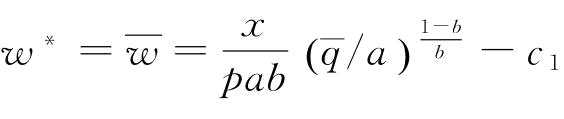 ,所以,∂2w*/∂p∂b>0;
,所以,∂2w*/∂p∂b>0;
(2)当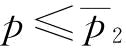 或
或 时,w*=w1,
时,w*=w1,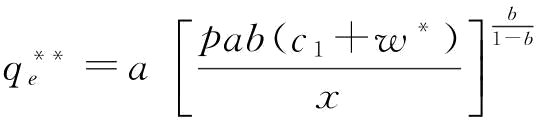 ,所以,
,所以,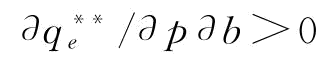 ;由推论4知,
;由推论4知,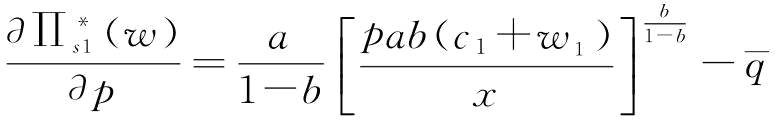 ,所以,
,所以,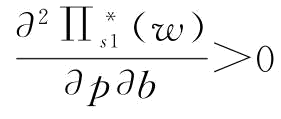 。
。
推论8可看出:
(1)当突发事件概率大于某个值时,随着突发事件概率的增大,供应商S1的最优订金减小,但是当恢复弹性系数增加时,最优订金减小的趋势在加速;当恢复弹性系数大于某一个值时,随着恢复弹性系数的增加,供应商S1的最优订金减小,但是当突发事件概率增加时,最优订金减小的趋势在加速;以上说明了突发事件概率和恢复弹性系数都比较大的情况下,供应商S2的恢复产量较多,供应商S1利用订金作为恢复的动力较弱。
(2)当突发事件概率小于某个值时,随着突发事件概率的增大,供应商S2的最优恢复产量增加,但还不到稳态下的最优产量,但是当恢复弹性系数增大,恢复产量增加的趋势在加速;当恢复弹性系数大于某一个值时,随着恢复弹性系数的增大,最优恢复产量增加,但还不到稳态下的最优产量,但是当突发事件概率增加时,最优恢复产量增加的趋势加速;以上说明了突发事件概率和恢复弹性系数都比较小的情况下,供应商S2的恢复产量较少,供应商S1利用订金作为恢复的动力较强。
(3)结合推论6,当突发事件概率小于某个值(图5-8中的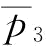 点)时,随着突发事件概率的增大,供应商S1的最优利润在减小(此时,订金的存在还不能弥补突发事件所带来的损失),但是当恢复弹性系数增大时,最优利润减小的速度在趋缓;当突发事件大于某一个值时,随着突发事件概率的增大,供应商S1的最优利润在增加,但是当恢复弹性系数增大时,最优利润增加的速度在加速;特别地,当突发事件概率等于某个值(图5-8中的
点)时,随着突发事件概率的增大,供应商S1的最优利润在减小(此时,订金的存在还不能弥补突发事件所带来的损失),但是当恢复弹性系数增大时,最优利润减小的速度在趋缓;当突发事件大于某一个值时,随着突发事件概率的增大,供应商S1的最优利润在增加,但是当恢复弹性系数增大时,最优利润增加的速度在加速;特别地,当突发事件概率等于某个值(图5-8中的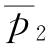 点)时,供应商S1的最优利润等于稳态下的最优利润。结合推论7,当恢复弹性系数小于某一个值时,随着恢复弹性系数的增大,供应商S1的最优利润在增加;当突发事件概率增大时,这种增加的趋势在加速。
点)时,供应商S1的最优利润等于稳态下的最优利润。结合推论7,当恢复弹性系数小于某一个值时,随着恢复弹性系数的增大,供应商S1的最优利润在增加;当突发事件概率增大时,这种增加的趋势在加速。
4)存在订金与不存在订金决策下的可靠供应商最优利润比较
接下来,我们进一步分析比较制定订金决策与不存在订金决策两种情况下的供应商S1最优利润,比较这两种情形下的供应商S1最优期望利润对突发事件概率的敏感性,并探讨恢复弹性系数对这种敏感性的影响。根据推论6,我们同样可以得到不存在订金下的突发事件概率p对最优期望利润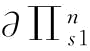 的影响,如推论9所示。
的影响,如推论9所示。
推论9:保持b不变:(1)当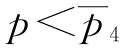 时,
时,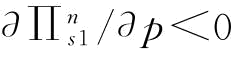 ;
;
(2)当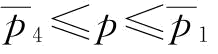 时,
时,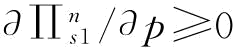 ;
;
(3)当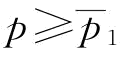 时,
时, ;
;
其中,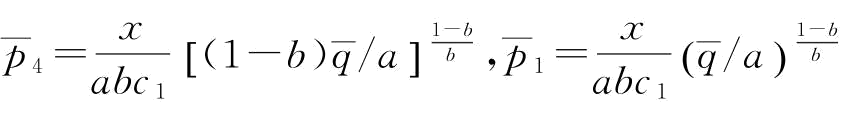 。
。
证明:式(5-12)对p一阶求导得:
其中,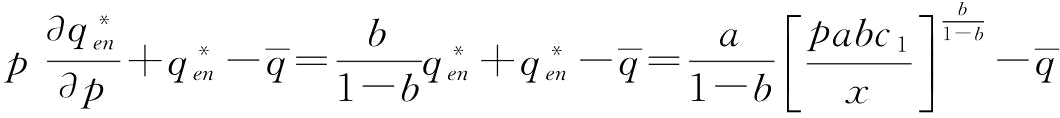 ;
;
当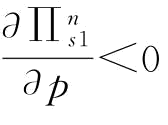 ;
;
那么,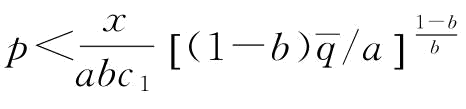 ;
;
当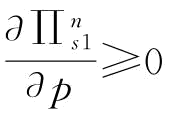 ;
;
那么,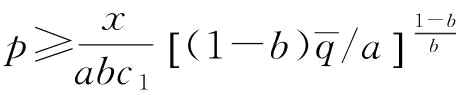 ;
;
由于,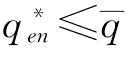 ;
;
则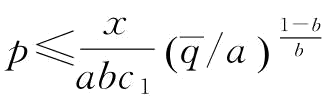 ;
;
令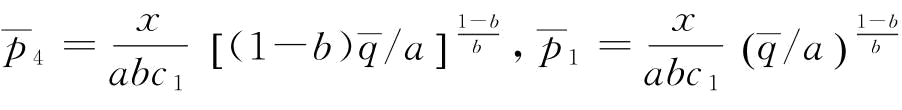 ,即可得到相关结论。证毕。
,即可得到相关结论。证毕。
比较图5-12和图5-13,可以发现:
当恢复弹性系数b增大时,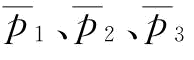 和
和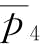 都变小;当恢复弹性系数小于某一个特定值时,
都变小;当恢复弹性系数小于某一个特定值时,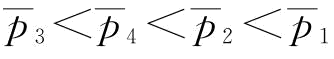 ;当恢复弹性系数大于某一个特定值时,
;当恢复弹性系数大于某一个特定值时,
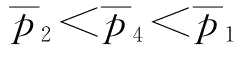 ;也就是说,当恢复弹性系统增大时,曲线
;也就是说,当恢复弹性系统增大时,曲线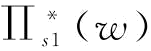 和
和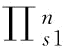 往左移,且曲线
往左移,且曲线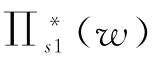 的利润最大值所对应的
的利润最大值所对应的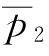 点比曲线
点比曲线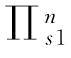 利润最小值所对应的
利润最小值所对应的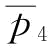 点往左移动速度要快;当
点往左移动速度要快;当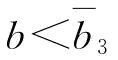 时,
时,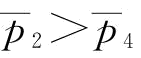 ;当
;当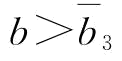 时,虽然
时,虽然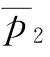 和
和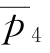 的值都在变小,但
的值都在变小,但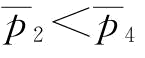 。
。
图5-12 当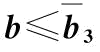 时两种情景下突发事件概率对供应商S1最优利润影响比较
时两种情景下突发事件概率对供应商S1最优利润影响比较
图5-13 当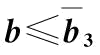 时两种情景下突发事件概率对供应商S1最优利润影响比较
时两种情景下突发事件概率对供应商S1最优利润影响比较
也就是说,当恢复效率较高时,面对小概率事件,存在订金情况下的供应商S1的最优期望利润可以恢复到稳态下的水平;但是不存在订金下的供应商S1的最优期望利润却处于一个相对较低的水平,这说明了应急援助恢复下,供应商S1的最优期望利润的水平与恢复效率以及是否有订金决策的存在有很大的关系。由推论6和推论9可以得到以下有关结论:
结论1:制造商所投入的援助恢复的效率越高,对供应商S1总是有利的;且当恢复效率较高时,供应商S1并不担心小概率事件;
结论2:保持恢复效率不变,不存在订金情况下,供应商S1对小概率事件较为敏感,而更偏爱大概率事件(因为突发事件的概率增加时,制造商提供应急援助恢复的动力在增强);存在订金情况下,供应商S1对小概率事件的敏感性有所减弱。
那么,当突发事件概率不变时,存在订金与不存在订金两种情况下,供应商S1对恢复效率如对恢复弹性系数的敏感性如何?相比较存在订金情况,如果不存在订金情况下的供应商S1的最优期望利润与存在订金情况的差距在减小,那么说明不存在情况下,供应商S1对恢复效率更加敏感。令Δπ为存在订金与不存在订金情况下的供应商S1的最优期望利润的差值,则由式(5-13)得:Δπ=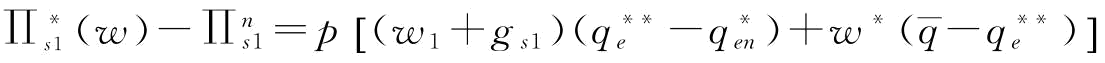 。
。
而b对Δπ的敏感性如推论10所示。
推论10:(1)当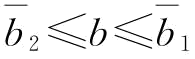 时,
时,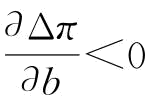 ;
;
(2)当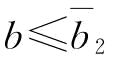 时,若
时,若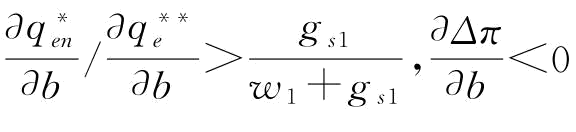 ;
;
证明:由推论7知,当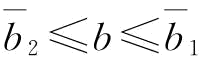 时,
时,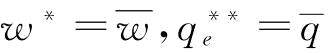 ;当
;当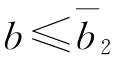 时,w*=w1,
时,w*=w1,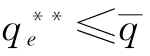 ;
;
(1)当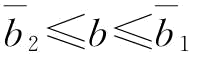 时,
时,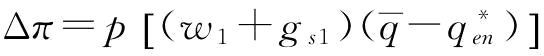 ,则
,则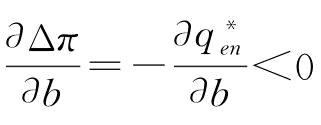 ;
;
(2)当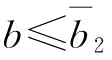 时,
时,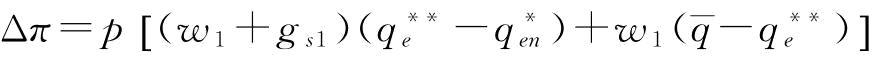 ;
;
那么,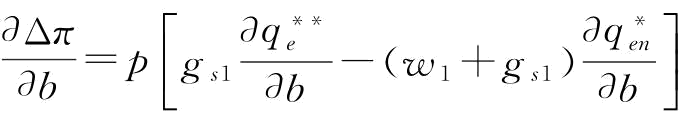 ;
;
分别令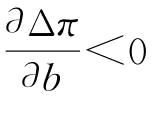 和
和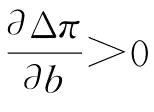 ,即可得到相关结论。证毕。
,即可得到相关结论。证毕。
由推论10可看出:
当恢复弹性系数较强,即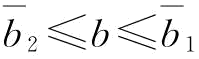 时,存在订金下的供应商S1的最优期望利润已经达到稳态下的水平,不存在订金下的供应商S1的最优期望利润达不到到稳态下的水平;此时,恢复弹性系数增大,存在订金下的供应商S1的最优期望利润不变(此时,最优订金在减小),但存在订金下的供应商S1的最优期望利润增加(此时,最优订金等于批发价)。所以,随着恢复弹性系数的增大,利润的差值在变小,即
时,存在订金下的供应商S1的最优期望利润已经达到稳态下的水平,不存在订金下的供应商S1的最优期望利润达不到到稳态下的水平;此时,恢复弹性系数增大,存在订金下的供应商S1的最优期望利润不变(此时,最优订金在减小),但存在订金下的供应商S1的最优期望利润增加(此时,最优订金等于批发价)。所以,随着恢复弹性系数的增大,利润的差值在变小,即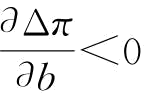 。
。
当弹性系数不足,即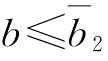 时,无论是否存在订金,供应商S2的恢复产量都达不到稳态下的水平,供应商S1的最优期望利润也达不到稳态下的水平。那么,两种情况下的供应商S1的最优期望利润差值对恢复弹性系数的敏感性要取决于两种情况下的最优恢复产量对恢复弹性系数的敏感性大小(这取决于供应链运营的成本参数及突发事件概率参数的大小),当不存在订金情况下的最优恢复产量对恢复弹性系数的敏感性大于存在订金情况下的敏感性的一定比例时,随着恢复弹性系数的增大,利润的差值在变小,即
时,无论是否存在订金,供应商S2的恢复产量都达不到稳态下的水平,供应商S1的最优期望利润也达不到稳态下的水平。那么,两种情况下的供应商S1的最优期望利润差值对恢复弹性系数的敏感性要取决于两种情况下的最优恢复产量对恢复弹性系数的敏感性大小(这取决于供应链运营的成本参数及突发事件概率参数的大小),当不存在订金情况下的最优恢复产量对恢复弹性系数的敏感性大于存在订金情况下的敏感性的一定比例时,随着恢复弹性系数的增大,利润的差值在变小,即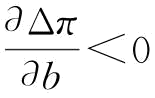 ;反之,利润的差值在变大。综合以上,我们可以得到结论3。
;反之,利润的差值在变大。综合以上,我们可以得到结论3。
结论3:保持突发事件概率不变,当恢复效率较高,或当恢复效率较低且不存在订金下的恢复产量对恢复效率的敏感性相对较高时,存在订金与不存在订金下的最优期望利润差值在变小,即不存在订金情况下,供应商S1对恢复弹性系数更敏感;当恢复效率较低,不存在订金下的恢复产量对恢复效率的敏感性相对较低时,存在订金与不存在订金下的最优期望利润差值在变大,即存在订金情况下,供应商S1对恢复弹性系数更敏感。
综合推论7和推论8,我们讨论订金决策在防范突发事件风险中的作用,如结论4所示。
结论4:当恢复效率较低时,不管有没有订金,供应商都担心小概率事件,即供应商对小概率事件是较为敏感的,可见援助恢复的效率决定了供应商面临的风险大小;当恢复效率较低或面对小概率事件时,订金的激励作用体现的较为明显;当恢复较高或面对大概率事件时,订金的激励作用体现的相对不明显。
假设在稳态下的供应链运营相关参数:r=10,w1=4,w2=2,gm=4,gs1=1,v=2,d服从于[240,280]的均匀分布。我们很容易求得稳态下的制造商最优订货量为: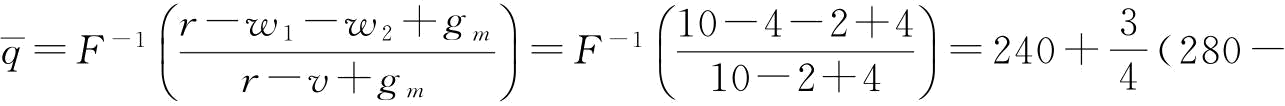 240)=270。
240)=270。
突发事件风险下,制造商M给不可靠供应商S2提供应急援助恢复,假设不可靠供应商S2恢复的产量为qe=t(e)=aeb=10e2/3(其中,a=10,b=2/3),单位援助恢复措施所花费资金x=1。我们可以得到供应商最优的应急援助恢复措施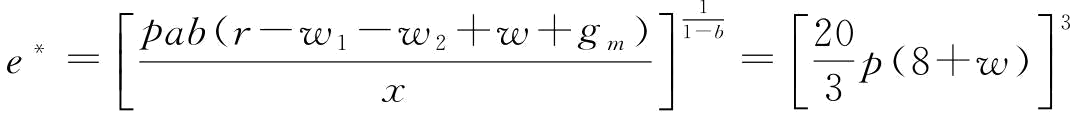 ,不可靠供应商S2最优恢复产量
,不可靠供应商S2最优恢复产量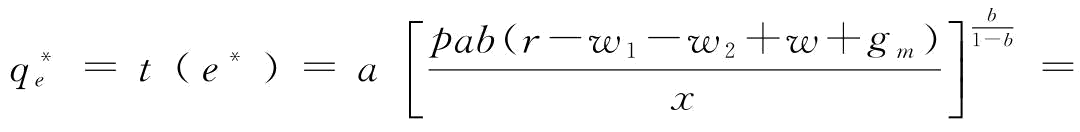
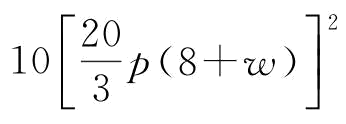 。
。
可以发现:可靠供应商S1制定的订金w越大时,可以激励制造商M投入更多的应急援助恢复措施。当然,w需要满足一定条件时,制造商M才有动力投入更多的应急援助恢复措施。由命题5知,w≤min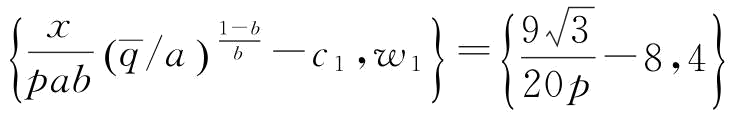 。根据命题6,我们可以得到供应商S1的最优订金w*,供应商S2的最优恢复产量
。根据命题6,我们可以得到供应商S1的最优订金w*,供应商S2的最优恢复产量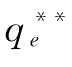 以及供应商S1的最优订金期望利润
以及供应商S1的最优订金期望利润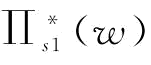 ;同理,也可以得到不存在订金下的供应商S2的最优恢复产量
;同理,也可以得到不存在订金下的供应商S2的最优恢复产量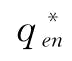 以及供应商S1的最优订金期望利润
以及供应商S1的最优订金期望利润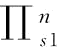 。接下来,我们分析突发事件概率对相关变量的影响。
。接下来,我们分析突发事件概率对相关变量的影响。
(1)p对w*的影响。由推论4知,当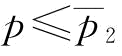 时,w*=w1=4;当
时,w*=w1=4;当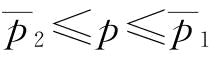 时,
时, ;
;
其中,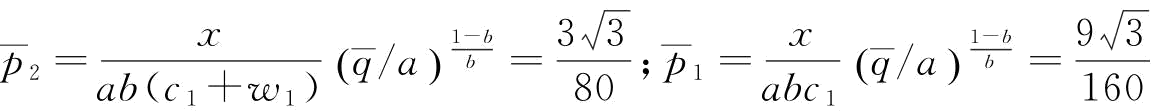 。p对w*的影响如图5-14所示。
。p对w*的影响如图5-14所示。
(2)p对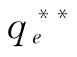 与
与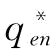 的影响。由推论5知,当
的影响。由推论5知,当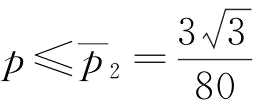 时,
时,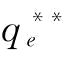 =64000*p2;
=64000*p2;
当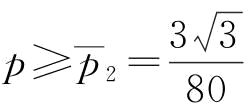 时,
时,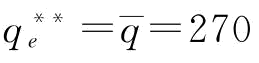 ;由推论3知,当
;由推论3知,当 时,
时,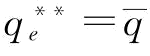 =270;
=270;
图5-14 突发事件概率对最优订金的影响
当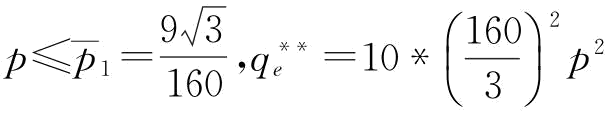 。p对
。p对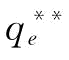 与
与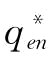 的影响如图5-15所示。
的影响如图5-15所示。
需要是说明的是,当存在订金时,订金本身是随着突发事件概率的变化而变化,有关订金与突发事件概率的相关性如图5-14所示。
图5-15 突发事件概率对最优恢复产量的影响
可以发现,供应商S1的最优订金一开始等于批发价,应急援助恢复下,供应商S2的产量在逐步恢复;随着突发事件的概率的增大,供应商S1的最优订金在小于批发价的情况下,就可以使得供应商S2的产量恢复到稳态下的水平。
(3)由推论6知,当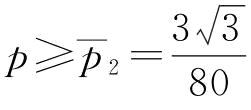 时,
时,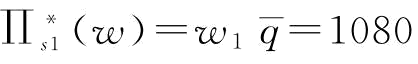 ;
;
当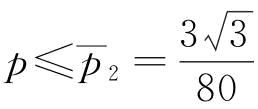 时,
时,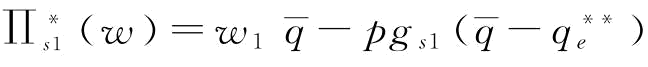 =1080-p[270-10(80p)2];
=1080-p[270-10(80p)2];
由推论9知,当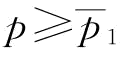 时,
时,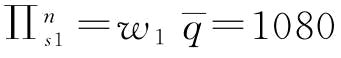 ;当
;当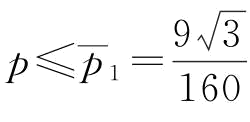 时,
时,
p对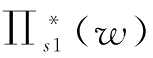 与
与 的影响如图5-16所示。同样,图5-16中,当存在订金时,订金与突发事件概率的相关性如图5-14所示。
的影响如图5-16所示。同样,图5-16中,当存在订金时,订金与突发事件概率的相关性如图5-14所示。
图5-16 突发事件概率对最优期望利润的影响
可以发现:①存在订金情况下的供应商S1的最优期望利润总是不小于不存在订金情况的最优水平,这说明制定订金决策对供应商S1总是有利的;②当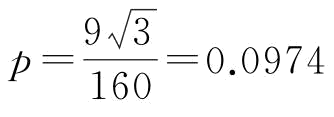 时,不存在订金情况下的供应商S1的最优期望利润可以得到稳态下的水平;当
时,不存在订金情况下的供应商S1的最优期望利润可以得到稳态下的水平;当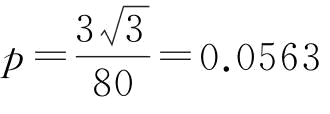 时,存在订金情况下的供应商S1的最优期望利润可以得到稳态下的水平。
时,存在订金情况下的供应商S1的最优期望利润可以得到稳态下的水平。
以上说明了:不存在订金情况下,供应商S1比较偏爱大概率事件,因为突发事件概率大小本事就是制造商投入应急援助恢复的动力;存在订金情况下,对供应商S1来说,其并不担心大概率事件,但是小概率事件的敏感性有所减弱,因为此时订金充当了制造商投入应急援助恢复的另外一个动力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




