该部分考虑的是当供应链上游企业供应商可能遭遇突发事件下,下游企业制造商为缓解供应中断风险,设计契约以引导供应商在事前进行恢复能力投资以便事后尽快恢复供应,主要研究供应商最优恢复能力投资并分析供应链协调所满足的条件。从研究问题的本身来看,这与文献Iyer et al(2005)、Hu et al(2012)类似;从契约设计来看,与Kim and Tomlin(2012)类似。与上述研究不同的是:
(1)Iyer et al(2005)设计的基于绩效的契约中,假定单位恢复时间的惩罚系数是常数;而在本文中是随机变量,我们主要考虑的是:在突发事件发生时间不确定以及特定的经营环境下制造商的商誉成本是不确定的。
(2)Iyer et al(2005)、Kim et al(2010)、Hu et al(2012)考虑通过下游企业设计恢复契约来激励上游企业合理投资恢复能力,但并没有说明契约中相关参数满足什么条件时,供应链能够协调。
(3)除了于辉等(2011)之外,其他文献都是假设供应链下游企业是风险中性的;我们假设供应链下游企业是风险规避的(风险规避程度直接影响到了恢复契约的设计),并引入CVaR风险度量准则来刻画企业在供应中断风险下的应急目标。
本章引入CVaR模型是建立在供应中断风险导致下游企业商誉成本不确定的基础之上;而于辉等(2011)的CVaR模型是建立在中断企业本身的单位额外生产成本不确定的基础之上。
我们考虑一个由供应商和制造商组成的供应链运营系统,其中供应商是不可靠的,即突发事件下,供应商的生产运营系统可能会中断从而导致制造商的零部件供应中断。假设该供应商的零部件具有专用性,制造商没有其他可替代的供应源,所以突发事件后供应商生产运营系统是否能够快速恢复直接关系到制造商的零部件的可获得性。由于资产专用性以及时间的紧迫性,供应商的生产运营系统的恢复需要预先进行恢复能力的投资。突发事件风险下,供应商对恢复能力进行投资的动力一方面来源于其自身的业务需求;另一方面则来源于制造商给予的压力,而制造商的压力来源于其自身的商誉成本较高。相关参数假定如下:
p:突发事件发生的概率;
λ:供应商的恢复能力投资的数量,包括运营设施中可用于修复所需要的维修技术、维修零配件和人员等;
k:单位恢复能力的成本;
b1:运营中断后供应商的单位时间商誉成本或机会成本;
b2+ε:运营中断后制造商的单位时间商誉成本或机会成本;其中,b2是常数,ε是随机变量,其均值为u、概率密度函数为f(.),分布函数为F(.)。
供应商的运营系统由于受到突发事件的冲击,需要进行事后恢复;X是运营系统从瘫痪状态到重新恢复到工作状态需要的时间,或称之为恢复完成时间。我们假设X服从于参数为λ的指数型分布,因此,X的期望值即平均的恢复时间是1/λ。由于在突发事件没有发生前,恢复能力投资需要成本,对于供应商来说,其恢复能力的投资成本需要从制造商那里得到一部分补偿。突发事件前,制造商不能直接观察到供应商的恢复能力选择λ,所以双方之间的契约关系并不能直接建立在λ的基础上,这是一个合理的假设,因为大多数供应商为防范生产运营中断而采取的预防措施(比如制定应对突发事件的预案、备用零配件的库存投资、对员工进行相应的生产设施恢复的培训、将生产运营系统的恢复工作外包给专业的服务企业等)很难监控。但是,制造商可以通过设计一个补偿契约来引导供应商对恢复能力的合理投资。Kim et al(2010)认为,补偿契约的设计可以建立在供应链恢复能力投资绩效(用恢复时间来表示)的基础上,并用转移支付函数T=w-θX表示制造商对供应商的补偿,其中w表示固定的转移支付,其独立于实现的绩效X;θ为单位X的惩罚系数。Kim et al(2010)考虑θ为常数,本章中我们将θ看成是随机变量,主要考虑的是制造商的经营绩效取决于制造商所处的经营环境以及运营中断后的恢复时间的长短,假设θ的均值为 、概率密度函数为g(.)、分布函数为G(.)。根据以上的描述以及相关参数假定,如给定恢复能力λ和制造商的转移支付T,供应商、制造商和供应链的期望成本函数分别为:
、概率密度函数为g(.)、分布函数为G(.)。根据以上的描述以及相关参数假定,如给定恢复能力λ和制造商的转移支付T,供应商、制造商和供应链的期望成本函数分别为:
其中,b2+Ε[ε]=b2+u,为制造商的期望商誉成本;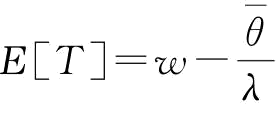 ,为实现绩效下的制造商的转移支付或补偿。
,为实现绩效下的制造商的转移支付或补偿。
对式(5-1)和式(5-3)进行优化,很容易得到:分权供应链下的最优恢复能力为 ;集权供应链下的最优恢复能力
;集权供应链下的最优恢复能力 。可以发现,当且仅当
。可以发现,当且仅当 时,λ*=λs;即当单位恢复时间期望惩罚系数等于制造商的单位中断时间(即恢复时间)所带来的期望商誉成本时,供应链进行协调状态。
时,λ*=λs;即当单位恢复时间期望惩罚系数等于制造商的单位中断时间(即恢复时间)所带来的期望商誉成本时,供应链进行协调状态。
以上分析了风险中性下的供应链恢复决策。然而,突发事件风险下,供应商的生产运营系统往往不可靠甚至遭到全面的破坏,下游企业将面临生产运营系统中断的风险。特别是在业务中断后商誉成本非常高的情况下,企业则存在退出某一业务单元的风险,这一点在高科技行业体现得尤为明显,如爱立信的案例。所以,在某些风险环境下,管理者对待风险的态度可能由中性趋向于规避,并在供应链应急决策中得到体现。VaR和CVaR是金融领域中度量风险最常用的两种准则,其中CVaR由于其良好的性能,近几年来得到的关注度越来越高,并有逐步代替VaR的趋势,且其在供应链风险领域的应用地位也在逐渐提高。有关VaR和CVaR两种度量准则我们在第3章已经进行了说明,这里不再赘述。
我们引入CVaR来刻画商誉成本不确定下的供应链的恢复能力决策目标。根据CVaR的一般定义[105],CVaR可以用来度量VaR所忽略的高于β分位数水平的超额平均损失,这也正是突发事件风险下决策者所关心的。假设决策者的风险规避系数或置信水平为β∈(0,1)(β越大,风险规避程度越高),损失的临界值为α,则突发事件下的供应链恢复能力投资决策的β-VaR模型可以刻画为:
根据β-VaR模型,则突发事件下的供应链恢复能力投资决策的β-CVaR模型可以刻画为:
式(5-5)度量的是大于β-VaR的超额平均损失,即β-VaR的条件期望损失。也就是说,决策者在运用CVaR刻画恢复能力决策目标时,是在假设其可能面临超额损失下对可能的应急措施进行优化。
令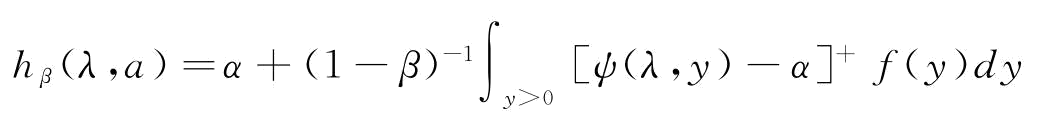 ,则有引理1。
,则有引理1。
引理1:hβ(λ,a)是关于α连续可微的凸函数,β-CVaR可以表示为
因此,供应链恢复能力决策的目标函数可以写成:
β-CVaR既可以对决策变量λ进行优化,同时又可以优化β-VaR中损失的临界值α,其优化的顺序为:先优化α,再将最优的α带入目标函数,并对λ进行优化。
命题1:β-CVaR下,对于给定的供应链恢复能力λ和决策者的风险规避参数β,存在一个最优的β-VaR临界损失值 ,使得
,使得 ;
;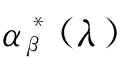 可以表示为:
可以表示为:
证明:由式(5-6)得, α)f(y)dy。求hβ(λ,a)对α的一阶偏导数得,
α)f(y)dy。求hβ(λ,a)对α的一阶偏导数得, F(aλ-kλ2-b)],由于hβ(λ,a)对α的二阶偏导数
F(aλ-kλ2-b)],由于hβ(λ,a)对α的二阶偏导数 =λ(1-β)-1f(aλ-kλ2-b1-b2)大于0,即hβ(λ,a)是α的凸函数,存在唯一的α使得hβ(λ,a)最小。令hβ(λ,a)对α的一阶偏导数
=λ(1-β)-1f(aλ-kλ2-b1-b2)大于0,即hβ(λ,a)是α的凸函数,存在唯一的α使得hβ(λ,a)最小。令hβ(λ,a)对α的一阶偏导数 ,可得到F(aλ-kλ2-b1-b2)=β,即有
,可得到F(aλ-kλ2-b1-b2)=β,即有 。证毕。(https://www.xing528.com)
。证毕。(https://www.xing528.com)
CVaR度量准则具有良好的计算性质,克服了VaR不具备决策所需要的优化性质,如可凸性,并能得到VaR度量准则下的临界损失决策的最优值。以下,对CVaR度量准则下的供应链恢复能力决策进行优化,并与风险中性情况进行比较。
命题2:β-CVaR下,供应链的最优恢复能力为
证明:将 带入式(5-6)得,
带入式(5-6)得,
分别求hβ(λ,a*)关于λ的一阶倒数和二阶导数。
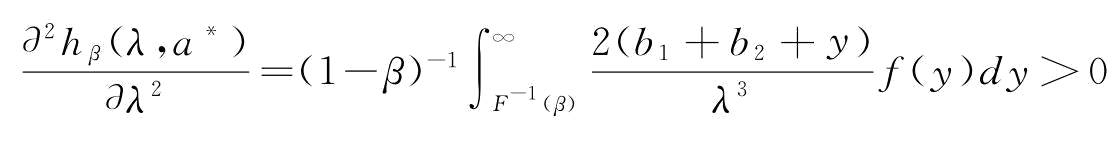 ,即hβ(λ,a*)是关于λ的凸函数。令
,即hβ(λ,a*)是关于λ的凸函数。令 ,可以求出β-CVaR下的供应链最优恢复能力
,可以求出β-CVaR下的供应链最优恢复能力 。
。
从前面的分析中知,β越大,即管理者的风险规避程度越高。以下,分析管理者风险态度对供应链最优恢复能力投资的影响,可以得到推论1。
推论1:突发事件风险下,管理者越是风险规避,其投入的最优恢复能力越大;风险中性是条件期望值的特例
证明:命题2得到了供应链的最优恢复能力 ,我们可以通过求
,我们可以通过求 对β的一阶导数来进行分析。
对β的一阶导数来进行分析。
即 是β的增函数。
是β的增函数。
从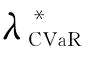 的表达式可以看出,当β=0时,
的表达式可以看出,当β=0时,
 ,而风险中性下,
,而风险中性下, 。所以,可以发现,风险中性是条件风险值的特例。
。所以,可以发现,风险中性是条件风险值的特例。
以下通过算例来分析。令p=0.1,b1=4,b2=4,k=2;θ服从于[0,10]的正态分布,其均值为4,标准差为2;β∈[0,0.9]。图5-1可看出,随着风险规避系数β的增加,供应链最优恢复能力 越大,当β=0时,风险中性是条件风险值CVaR的特例。所以,风险规避下的最优恢复能力的投资严格不小于风险中性情况。
越大,当β=0时,风险中性是条件风险值CVaR的特例。所以,风险规避下的最优恢复能力的投资严格不小于风险中性情况。
图5-1 风险规避系数对供应链最优恢复能力的影响
以上,我们的分析是建立在集权供应链环境下的,即将供应链上下游企业看成是一个整体。那么,在分权供应链下,供应商所投入的最优恢复能力是否能达到集权供应链的恢复能力投入的标准,如果能,如何协调供应链?
分权供应链下,恢复能力变量λ是供应商的决策变量。在前面的模型中,我们分析了在风险中性下,当单位恢复时间期望惩罚系数等于制造商的单位中断时间(即恢复时间)所带来的期望商誉成本时,供应链达到协调。那么,在条件风险值(β-CVaR)度量准则下,制造商会将其面临的商誉成本的信息传达给供应商,并将此作为对供应商进行惩罚的依据。β-CVaR下,制造商的风险规避程度(用β表示)是由其商誉成本b2+ε的大小来决定的,也就是说,制造商会将自身对突发事件下供应中断的风险态度传达给供应商。
根据前面对供应链恢复能力投资决策的β-CVaR模型的分析,我们很容易建立分权供应链下供应商恢复能力投资决策的β-CVaR模型。令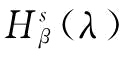 为供应商恢复能力决策下的目标函数,则有
为供应商恢复能力决策下的目标函数,则有
其中,g(x)为单位时间的惩罚系数θ所服从的密度函数;
ψs(λ,x)为建立在惩罚基础上的供应商损失/成本函数;
αs为供应商设定的损失临界值。
同样,我们可以得到分权供应链下供应商的最优恢复能力以及供应链协调所满足的条件,如命题3和推论2所示。
命题3:β-CVaR下,供应商的最优恢复能力为
推论2:满足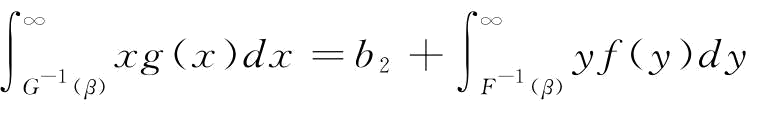 时,供应链进入协调状态
时,供应链进入协调状态
由于篇幅所限,命题3的证明可以参考命题2,具体证明过程省略。
通过对命题2中的 的表达式和命题3中的
的表达式和命题3中的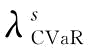 表达式进行比较分析,很容易推论2的结果,即当满足
表达式进行比较分析,很容易推论2的结果,即当满足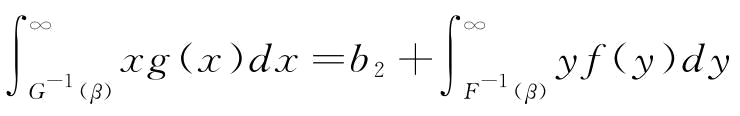 时,
时,
 。也就是说,当单位中断时间(恢复时间)的惩罚系数的条件期望值等于单位时间中断时间(恢复时间)的商誉成本的条件期望值时,分权供应链与集权供应链下的最优恢复能力投资是相等的,即供应链进入协调状态。
。也就是说,当单位中断时间(恢复时间)的惩罚系数的条件期望值等于单位时间中断时间(恢复时间)的商誉成本的条件期望值时,分权供应链与集权供应链下的最优恢复能力投资是相等的,即供应链进入协调状态。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




