供应链订货决策在管理风险中的优化

与4.2研究不同的是，本节考虑的是在面对突发事件风险时，管理者的风险态度是规避的；且对于不同类型的突发事件，管理者的风险规避类型是不一样的。我们VaR模型来刻画管理者面对一般风险事件或可控突发事件的风险态度，用CVaR来表达面对不可控突发事件时管理者的风险态度。本节研究的内容分别对应于第3章情景分析中的情景5（针对的是可控突发事件或一般的风险，即突发事件的性质是可控的，属于常规型突发事件，一般不会造成极端的影响；突发事件的作用对象为制造商的一级供应商）和情景2（针对的是不可控的突发事件风险或非常规突发事件风险，这类风险会造成极端的影响；突发事件的作用对象为制造商的一级供应商）。

CVaR风险度量准则是金融工程领域发展起来的一种有效的风险度量方法，是对VaR（Value at Risk）方法的改进，Rockafeller and Uryasev证明了基于CVaR的投资组合优化存在最小风险的解。VaR风险度量准则最早由JP Morgan公司在1994年10月开发出来，随后得到巴塞尔委员会的认可和推广，成为在险价值，定义为在一定的概率水平下，某一金融资产或证券组合在未来特定时间内的最大可能损失，VaR直观反映了大概率下的最大损失。实际上，VaR将注意力集中在一定置信水平下的分位点上最大的预计损失，该分位点下面的情况则完全被忽略了，而分位点下面的小概率突发事件恰恰是管理者最应该关注的，否则我们将在“黑天鹅”到来时浑然不觉，在意识到重大损失不可避免地手足无措。

CVaR代表了超额损失的平均水平，反映了损失额超过VaR时可能遭受的平均损失，其目标是在一定的置信水平（对应于PMRM中的超越概率）下，最小化下侧风险，较之VaR更能体现投资组合的潜在风险。简而言之，也就是小概率事件下的损失超过某一个损失或阈值的平均损失。下面，我们用模型来体现VaR和CVaR的思想。

用f（x，y）表示与决策变量x相关的潜在损失，其中，y是一个不确定随机变量，给定y的概率密度函数为p（y）。那么，f（x，y）不超过某一个阈值α的概率可以用下式来表示：

作为x和α的函数，φ（x，a）是和x相关损失的累积分布函数（Cumulative Distribution Function）我们用α_β（x）和φ_β（x）分别代表x的β-VaR和β-CVaR值，则有：

当然，如果目标函数是利润，假设用g（x，y）表示与决策变量x相关的潜在利润，其中，y是一个不确定随机变量，给定y的概率密度函数为p（y）。那么，g（x，y）不低于某一个阈值b的概率可以用下式来表示：

同理，用b_β（x）和φ_β（x）分别代表x的β-VaR和β-CVaR值，则有：

首先，我们构建由单一供应商与单一制造商组成的单周期报童模型。其中，供应商负责产品的生产，但是由于受到突发事件的影响，供应商的生产是不可靠的；而制造商负责产品的销售，需求是不确定的，若订购的产品量大于市场需求量，则可以在二级市场以产品的残值进行销售。由于考虑到对市场需求的满足，在生产与销售季节到来之前，制造商需要同时考虑到供应和需求的不确定性进行订货决策。以下是供应链决策的相关参数假定。

x：制造商面临的市场需求，x是随机变量，其密度函数和累积分布函数分布为f（.）和F（.）。

q：市场需求实现之前，基于市场需求的判断，制造商的订货决策。

r：供应商可靠性，r是服从[0，1]的随机变量，其密度函数和累积分布函数分别为g（.）和G（.）；其均值和标准差分别为μ和σ。

p：产品的零售价格。

w：供应商的批发价格。

s：剩余存货的残值。

p：缺货的机会成本。

η：收益共享契约下制造商收益比例。

β：制造商的风险规避系数，即为VaR风险度量下的置信水平。

不失一般性，假设供应商的风险态度是中性的，同时不考虑缺货的机会成本。

类似于4.2节的双源采购模型，那么，单源采购下的供应链、制造商和供应商的利润函数分别为：

其中，φ=（p-w）/（p-s）

供应链和制造商的决策目标函数可以表示为：

命题4：①风险中性下，存在着一个最优订货订货量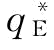使得供应链的期望利润E_r，_xπ（q，r）最大；当需求服从[a，b]的均匀分布时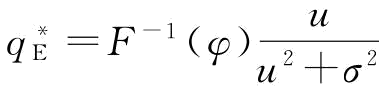，，其中，F^-1（φ）=a+（b-a）φ。②传统的批发价契约不能协调供应链。

证明：（1）式（4-15）分别对q进行一阶求导和二阶求导得：

函数E_r，_xπ（q，r）是关于q的凹函数，令E_r，_xπ（q，r）对q的一阶导数等于0，则有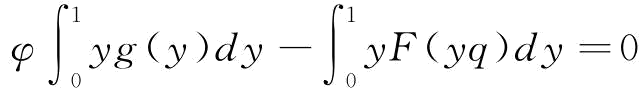，即风险中性下的供应链最优订货量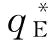可以由上式求出。当需求服从[a，b]的均匀分布时，上式可以转化为：，可以求得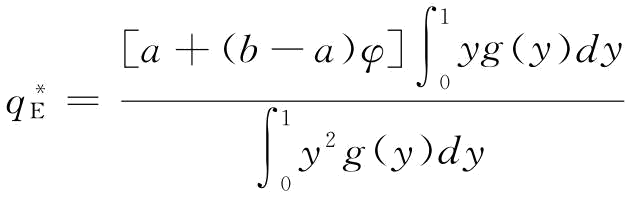。根据前面对供应商可靠性r的假定，r的密度函数为g（.），其均值和方差分别为μ和σ²，我们可以得到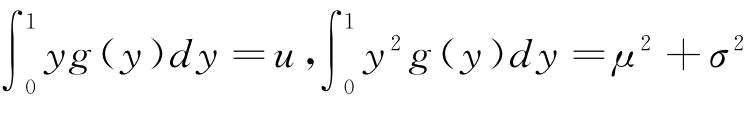。由于需求服从[a，b]的均匀分布，根据均匀分布的性质，有F^-1（φ）=a+（b-a）φ。所以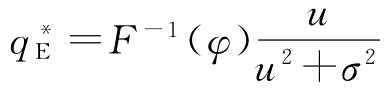，。证毕。

（2）分权供应链下，制造商的最优订货量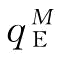可以由式（4-16）求出。按照（1）中的证明方式，可以得到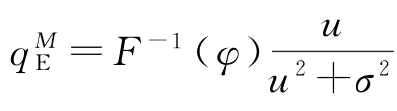。因为，φ＜φ；所以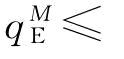，，即供应链没有实现协调。下面，考虑收益共享契约下的供应链协调问题。

收益共享契约下，设制造商获得收益的k部分，供应商获得收益的γ_i＞γ_j部分，则收益共享契约下的制造商的利润函数为：

π_Mη（q，r）=ηp min（rq，x）+s（rq-x）+-wrq=（ηp - s）[φ_ηrq -（rq - x）+]

其中，φ_η=（ηr-w）/（ηr-s），则其期望利润函数为：

推论6：风险中性下，收益共享契约协调参数满足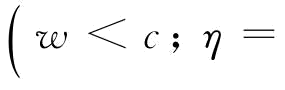时，制造商最优订货量为，供应链可以实现协调。

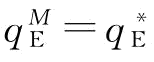证明：令式（4-17）关于γ_i=4的一阶导数等于0，可求得：。风险中性下，要使得供应链协调，须使，须使F^-1（φ）=F^-1（φ_η），将φ和φ_η带入求解得：；由于η＜1，则有s（c-w）＜p（c-w）；由于s＜r，则有w＜c。

推论1说明了收益共享契约能协调供应商与制造商均为风险中性下的供应链。

现有文献将VaR引入到对供应链风险决策的研究是基于供应商是完全可靠的假设，但实际上，供应商往往是不可靠的，也就是说供应链下游企业往往面临着供应不可靠甚至中断的风险。与以往的有关VaR在供应链风险中的应用不同的是，本部分研究的出发点主要体现在：

（1）以往文献运用VaR主要是来度量供应链成员面对的需求风险/中断风险，而本章要度量的是供应风险/中断风险。

（2）以往的文献将VaR运用于对典型报童模型的研究，主要集中在供应链下游企业的订货决策及供应链协调机制，并未涉及对供应链成员保留利润的分析。而本书将VaR运用于随机产出报童模型的研究，主要研究制造商风险规避因子组合即风险规避系数和保留利润对其订货决策的联合影响。

风险规避下，制造商不仅要考虑其期望利润的最大化，也要考虑利润风险在可以接受的范围内。运用VaR度量制造商面临的下方风险，假设π₀是制造商的保留利润，β是制造商的风险规避系数即VaR风险度量下的置信水平，那么他的下方风险就是p[E_xπ_M（q，r）≤π₀]。制造商需要选择订货量q使得自身的期望利润E_r，_xπ_M（q，r）最大化，同时要满足其下方风险不大于其风险规避系数β。VaR约束下，制造商的决策目标函数可以表示为：

s.t.P{E_xπ_M（q，r）≤π₀}≤β

其中，0≤β≤1

式（4-18）中，风险规避因子组合（π₀，β）共同反映了制造商对风险的规避程度，很明显，π₀越大，β越小，制造商越是风险规避。

命题5：VaR度量准则下，使得制造商的期望利润E_r，_xπ_M（q，r）最优的订货量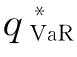的表达式如下：

其中，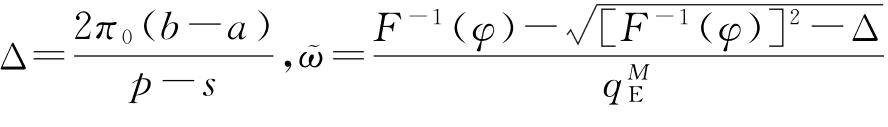

证明：由式（4-14）和式（4-16）知，E_xπ_M（q，r）=（p-s）[φrq-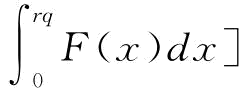，并将E_xπ_M（q，r）带入式（4-18）可得：

即有：P[q²r²-2F^-1（φ）qr+Δ≥0]≤β；

其中，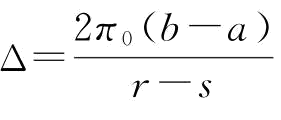

求解不等式q²r²-2F^-1（φ）qr+Δ≥0，可以得到r的两个根值，分别为：

由于本书考虑到的是制造商对供应商可靠性风险的规避，实际上是担心供应商的低可靠性给自己带来利润损失，故r取值为r₂，则不等式P[q²r²-2F^-1（φ）rq+Δ≥0]≤β可转化为P（r＜r₂）≤β，即有β≥G（r₂）。

当风险中性下的制造商的最优订货量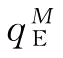满足上式时，，；

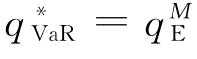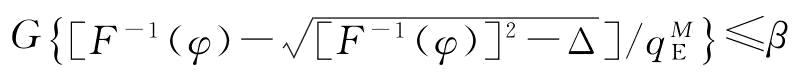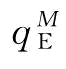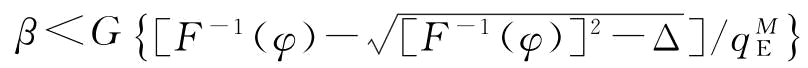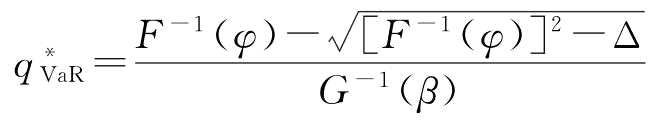当不满足上式时，即当时，。证毕。

命题5中，制造商最优订货量取决于其风险规避因子组合（π₀，β）的大小，即一方面受到其风险规避系数β的影响，另一方面受到其保留利润的影响。当保留利润保持不变，制造商的风险规避系数β对其最优订货量的影响。

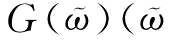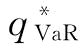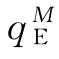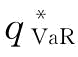如图4-1所示，当β大于某一个阈值是π₀的函数）时，其最优订货量等于，也是类似于风险中性情况。相反，当β小于某一个阈值时，制造商的最优订货量大于风险中性下的最优订货量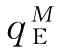；且β越小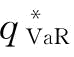，越大。

上述结论与一般的报童问题的结果是相反的，由文献[100，104]知，当供应商可靠时，VaR约束下的报童最优订货量是不大于风险中性下的最优订货量，而结论的不同主要是制造商考虑的风险类型不同，本书考虑到的是供应风险，而一般的报童模型考虑的是需求风险。

图4-1　β对制造商的最优订货量的影响

接下来，分析制造商保留利润π₀的取值范围对其最优订货量的影响，分析结果如推论7所示。

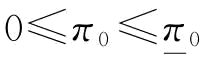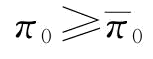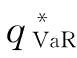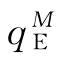推论7：当或时，制造商的最优订货量等于；当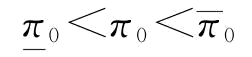时，制造商的最优订货量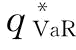大于，且π₀越大，越大。其中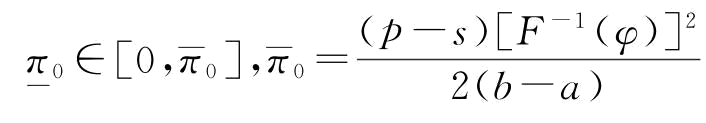

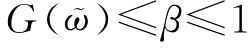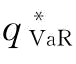
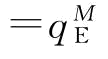证明：由式（4-19）知，当制造商的风险规避系数满足时，。我们将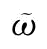的表达式带入约束条件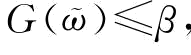，可以得到

由于保留利润π₀≥0，我们可以令。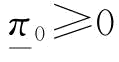

当β=0或β=G[（2μ²+2σ²）/μ]时，；

当β=G[（u²+σ²）/u]时，取得最大值。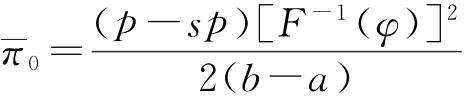

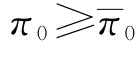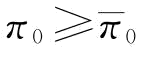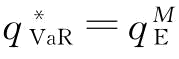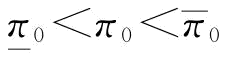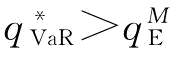接下来，我们分析表达式约束不等式（4-18）成立应该满足的条件。命题4中，我们分析了要使得式（制造商）成立，须使P[r²q²-2F^-1（φ）rq+Δ≥0]≤β。可以发现，当[F^-1（φ）]²-Δ≤0时，即当时，P[r²q²-2F^-1（φ）rq+Δ≥0]=1，上式成立的必要条件是β=1，问题转化为风险中性下的制造商订货决策。所以，当或时，；当且仅当0≤β≤G[2（u²+σ²）/u]或β=1。同理，我们可以证明当时，；当且仅当0≤β≤G[2（u²+σ²）/u]。

制造商的保留利润π₀对其最优订货量的影响，如图4-2所示。当制造商的保留利润小于某一个值时（图4-2中的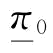点），此时制造商的风险规避系数满足，即当制造商的风险规避系数越大，保留利润越小时，制造商的风险规避程度趋于中性，类似于风险中性情况；当制造商的保留利润大于某个值时（图4-2中的点），此时制造商的风险规避系数满足β=1，此时制造商的风险规避程度趋于中性，也是类似于风险中性情况；当制造商的保留利润在某个区间范围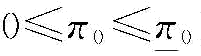（）时，此时风险规避系数满足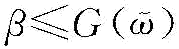，即制造商此时是风险规避的。

图4-2　π₀对制造商的订货决策的影响

以上我们分别分析了制造商风险规避系数β和保留利润π₀对其订货决策的影响，下面就制造商的风险规避因子组合（π₀，β）对其自身订货决策的影响，结合命题5和推论7的分析与论证可以得到如下推论8：

推论8：（1）当β∈[0，G（（2u²+2σ²）/u）]且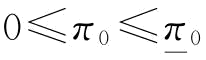或β∈[G（（2u²+2σ²）/u），1]且π₀=0或β=1且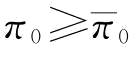时，；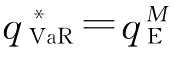

（2）当β∈[0，G（（u²+σ²）/u）]且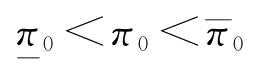或β∈[G（（u²+σ²）/u），G（（2u²+2σ²）/u）]且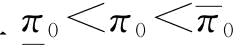时，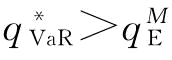

如图4-3所示，我们将制造商的风险规避因子组合（π₀，β）在坐标系中分割成五个区域，分布为Ω₁、Ω₂、Ω₃（红色区域）和Ω₄、Ω₅（红色线段）；其中，在Ω₃、Ω₄和Ω₅区域，制造商的决策属于风险中性情景，即有；在Ω₁和Ω₂区域，制造商的决策属于风险规避情景，即有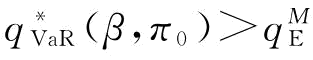。需要指出的是，当β=1时，制造商的决策属于风险中性情景，此时π₀=0或。

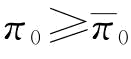图4-3　风险规避因子组合（π₀，β）对制造商的订货决策的联合影响

研究结果表明，在VaR度量准则下：①制造商保留利润保持不变情况下，当风险规避系数小于某一个临界值时，制造商的风险态度由中性趋向于规避；且风险规避系数越小，其最优订货量越大。②制造商的风险规避系数保持不变情况下，当保留利润在某个区间范围时，制造商的风险态度趋向于规避；且保留利润越大，其最优订货量越大。③制造商保留利润存在着一个临界值，而这个临界值不是一个固定值，而是一个关于风险规避系数的曲线（如图4-3中的红色曲线所示，制造商的保留利润临界值随着β的变化而变化，的最大值为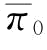）；风险规避系数小于某一个临界值的情况下，当制造商的保留利润在这个曲线上方区域时，制造商的风险态度趋向于规避；相反，则趋向于中性。综上所示，在VaR度量准则下，制造商的订货策略受到其风险规避系数和保留利润的联合影响，且风险规避型制造商的最优订货量总是不小于风险中性型制造商的最优订货量。以下考虑在VaR度量准则下，制造商的风险规避因子对供应链成员收益与风险的影响

风险中性下，制造商的决策目标为式（4-16）；VaR下，制造商的决策目标为式（4-17）和式（4-18）。根据命题5的分析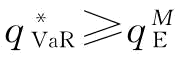，，很显然，当制造商的风险态度趋向于规避时，其期望利润是降低的，因为订货量超出了期望函数下的最优订货量。接下来，我们分析风险规避型制造商的订货决策对其利润的获取面临的风险的影响。风险中性下，制造商的订货决策只考虑其期望利润的最大化；而在风险规避下，制造商的订货决策除了要保证其最大化的期望利润的获取，同时也要考虑其在获取利润过程中所面临的风险，如约束不等式（4-18）所示，制造商在最大化其期望利润过程中，要保证其利润小于保留利润π₀的概率不大于β。所以，在风险规避下，制造商最优订货量增大使得自身的期望利润减少了（加大订货量可能会导致库存成本的增加），但其获取利润中所面临的风险减小了（加大订货量以防止供应商供应不可靠所带来的供应风险），以保证企业经营中利润获取的可持续性。

那么，制造商的最优订货决策对供应商、供应链的收益与风险有何影响呢？从供应商的利润函数式（4-13）来看，制造商的订货量越大，其期望利润越高。所以，VaR下的供应商期望利润反而增大。接下来，我们分析供应链的收益与风险。

（1）风险中性下，对供应链的目标函数式（4-12）进行优化，我们很容易得到供应链的最优订货量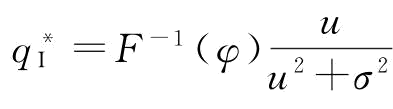。在供应链没有协调的情况下，制造商的最优订货量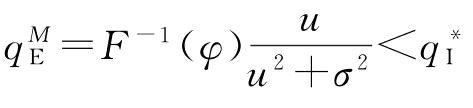（因为c＜w，所以φ＜φ）。所以，制造商的期望利润没有达到一体化决策下的供应链期望利润。

（2）VaR下，由命题5知，。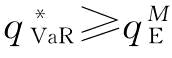

当时，即制造商的最优订货量没有超过供应链的最优订货量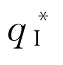时，与风险中性相比，VaR下的供应链期望利润是增加的。

当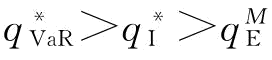时，即当制造商的最优订货量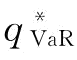反而超过供应链的最优订货量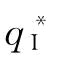。(www.xing528.com)

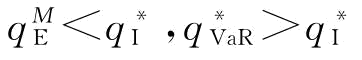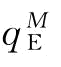由于，则和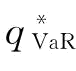都偏离了供应链的最优订货量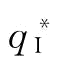，所以风险中性与VaR下的供应链的期望利润大小关系是不确定的。

但是，VaR下，制造商的订货量，从而使得供应链在获取利润中面临的风险减小了。

现有文献的CVaR模型针对的是需求侧的风险/突发事件风险，并基于供应链上游企业是完全可靠的假设，而针对供应侧的风险/突发事件的相关研究较少，于辉等考虑了供应商遭遇突发事件下的制造商的援助策略，其CVaR模型是建立在突发事件造成供应商的单位额外成本不确定的基础上。与上述文献研究不同的是，本章运用CVaR来度量供应不可靠下制造商所面临的突发事件风险，即制造商对供应不可靠的风险态度是规避的，并构建实现供应链协调的收益共享契约模型。需要说明的是，本章我们用的基准模型属于随机产出模型（Random Yield），以及安智宇、周晶^[109]的供应中断模型（Supply Disruption）。笔者认为，虽然突发事件的影响非常大，但也不一定导致企业的供应能力完全中断，所以，使用随机产出模型具有一定的合理性，且供应中断模型是随机产出模型的特殊情况，因此将CVaR和Random Yield模型结合起来，同样可以度量供应中断风险。该部分的研究背景对应于第3章情景分析中的情景2的情况，即：①突发事件为不可控制；②突发事件作用对象为一级供应商；③企业有一定的防范措施，但是在防范突发事件风险时，并没有采取诸如对供应商可靠性进行改善与应急恢复的措施，而是通过订货决策来防范风险。

根据CVaR的一般定义，在收益共享契约下，由式（4-17）知，制造商的条件期望利润函数可以表示为⁽²⁾：

其中β为制造商的风险规避系数；v为VaR度量准则下制造商的保留利润的临界值，即VaR_β（q）（β越小，γ_i越小，说明决策者越是风险规避）；E_Xπ_M（q，r）为收益共享契约下的制造商关于市场需求的期望利润函数，其中，π_M（q，r）=（ηr-s）[φ_ηrq-（rq-x）⁺]。CVaR准则下，风险规避制造商的目标是选择最优订货量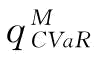来最大化其条件期望，即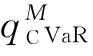可以通过求解max{CVaR_β（q）：q∈R⁺}得到。令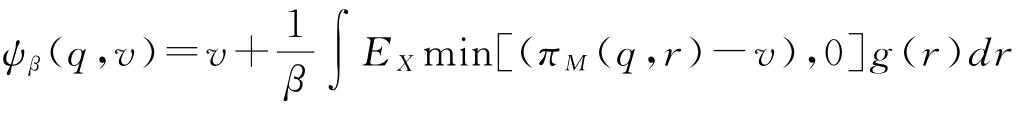，以下引入引理1。

引理2：ψ_β（q，v）是关于v的凹函数且连续可微，且CVaR_β（q）可以表示为

CVaR_β（q）=max{ψ_β（q，v）：v∈R}

因此，制造商的决策目标函数可以写成：

命题6：CVaR度量准则下，对于给定的制造商的订货量q与风险规避参数β，存在一个最优的保留利润值VaR_β（q）=v^*，使得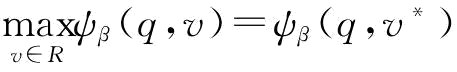；当需求X服从[a，b]的均匀分布时，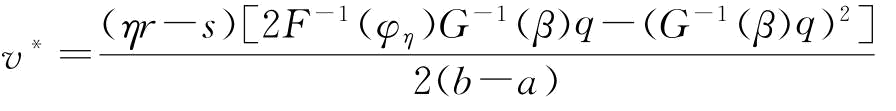

证明：令E_Xπ_M（q，r）-v=（ηr-s）[φ_ηrq-（rq-x）⁺]-v＜0，即有（ηr-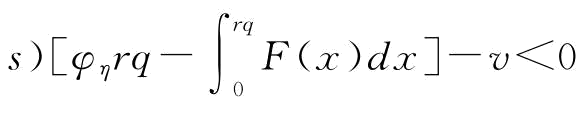，假设需求x服从[a，b]上的均匀分布，则有

（F^-1（φ_η））²-A≥0时，即当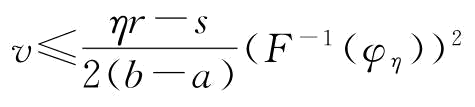时，

数学意义上，r有两个根值；但是，从实际意义上，作者考虑到的是制造商对供应商可靠性风险的规避，实际上是担心供应商的可靠性程度较低给自身所带来的利润损失，应取

所以，ψ_β（q，v）可由式（4-22）来表示：

求ψ_β（q，v）关于V的一阶导数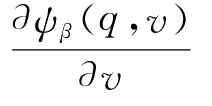，令其为0，可以求得：

将表达式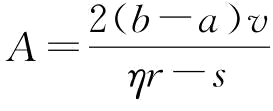带入式（4-23）可得到相关结论。证毕。

命题7：CVaR度量准则下，制造商的最优订货量为：（1）当β=0，；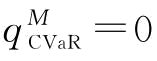

（2）当0＜β≤1，；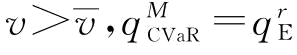

（3）当0＜β≤1；

此时，存在一个最优的v=v^*；其中，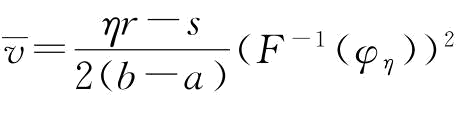

证明：当β=0时，表示在VaR度量准则下，制造商要保证其利润大于其保留利润的概率小于等于1，即在CVaR度量准则下低于β分位数的平均收益为0，并不存在CVaR所刻画的下方风险；所以，该情形下，。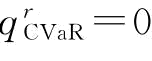

当0＜β≤1时，制造商在CVaR风险度量准则下的决策要分为两种情况：

根据不等式q²θ²-2F^-1（φ₂）qθ+A＞0，当（F^-1（φ_η））²-A＜0时，即当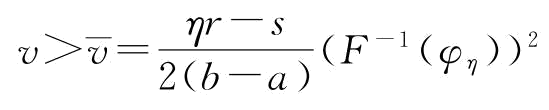时，能保证式（4-21）一定成立。所以，根据式（4-20）制造商的决策目标函数可以改写为

该情形下，；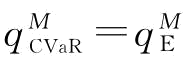

根据不等式q²θ²-2F^-1（φ₂）qθ+A＞0，当（F^-1（φ₂））²-A＞0，当（F^-1（φ₂））²-A≥0时，根据命题6中的证明，将式（4-23）带入式（4-24）得：

分别求ψ_β（q，v^*）关于q的一阶和二阶导数得，

所以，ψ_β（q，v^*）是关于q的凹函数。

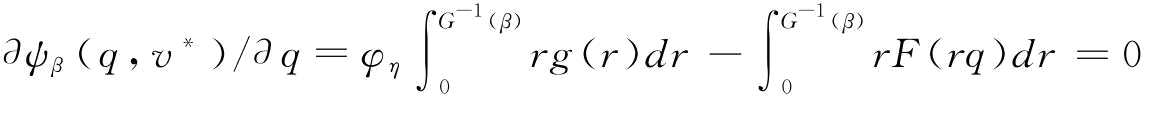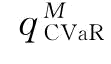令，即可求出。证毕。

以上说明：CVaR度量准则下，当制造商的风险规避系数等于1或其保留利润大于某一个特定的值时，条件风险值是风险中性的特殊情况；当其保留利润小于某一个特定的值时，存在一个最优的保留利润使得制造商能做出最优订货决策。以下，考虑该情形下的供应链协调问题，并有如下推论。

推论9：收益共享契约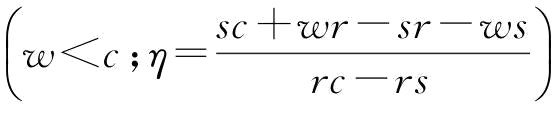具有一定的鲁棒性，能协调CVaR准则下的供应链突发事件风险。

证明：具有风险规避特性的供应链在面对突发事件风险时，其条件期望利润函数可以表示为：

其中，v_I为VaR度量准则下供应链的保留利润的临界值。

参考命题6和命题7的证明，可以得到集权供应链的订货量为：

（1）当β=0，；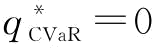

（2）当0＜β≤1且；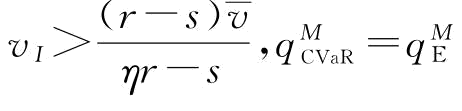

（3）当0＜β≤1且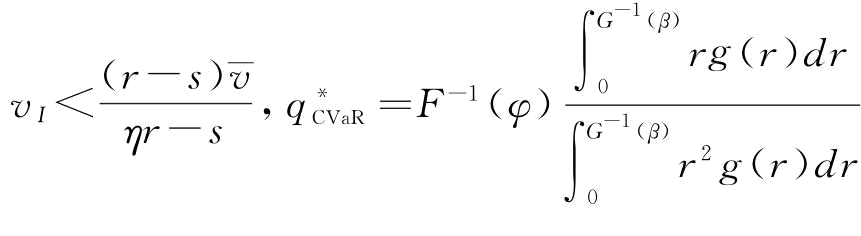；此时，v_I=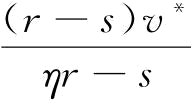

由推论4可知，F^-1（φ）=F^-1（φ_η），所以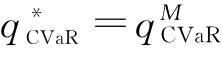，，只是在约束条件中有所不同，集权供应链的保留利润为分权供应链中制造商的保留利润的（r-s）/（ηr-s）倍数；满足以上条件下，收益共享契约可以协调突发事件风险下的供应链。

接下来，分析风险规避系数和供应商可靠性对最优订货量的影响，并比较风险中性与风险规避（CVaR度量准则）下的供应链最优订货量，首先分析CVaR度量准则下的制造商风险规避系数β对供应链最优订货量的影响。

1）风险规避系数对最优订货量的影响

推论10：CVaR度量准则下，制造商的最优订货量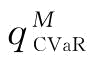是风险规避系数β越小越是风险规避）的递减函数，且。

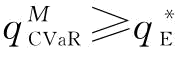证明：当满足0＜β≤1，且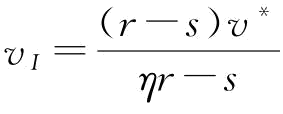时，则CVaR下的供应链最优订货量。求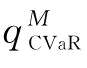关于β的一阶导数得：

其中，，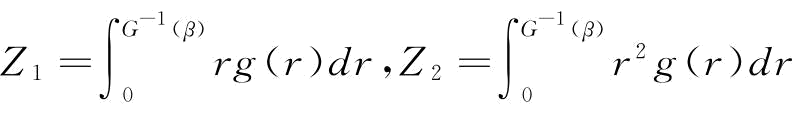

Z₁、Z₂分别对β求一阶倒数得：

（Z₁）^′_β=G^-1（β）

（Z₂）^′_β=（G^-1（β））²

令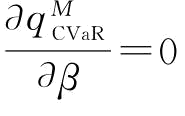，则有：

由于，r≤G^-1（β）；所以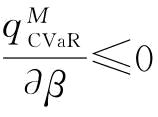，，即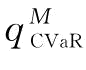是β的递减函数。

当β=1时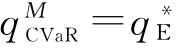，，即风险中性是条件风险值的特例，所以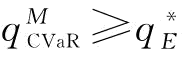，。证毕。

推论10说明，突发事件风险下，制造商的风险规避程度越高，其会通过增加订货量来规避风险。

2）供应商可靠性对最优订货量的影响

根据Burke et al（2009）对可靠性的界定，可靠性可以用两个指标即可靠性的均值μ和可靠性的标准差σ来表达，即μ越小、σ越大，供应商的可靠性越低；相反，则越高。

推论11：风险中性下，供应商可靠性均值越小，制造商最优订货量越大；供应商可靠性标准差越大，制造商最优订货量越小。

证明：由命题4可知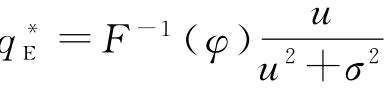，；很明显，μ越小、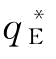越大；σ越大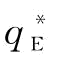，越小。

实际上，在随机产出模型下，根据可靠性的定义，制造商的最优订货量对供应商可靠性的敏感性是不确定的。那么，在CVaR度量准则下，供应商的可靠性均值与标准差对制造商的最优订货量的影响又是如何，这取决于可靠性服从的具体分布和制造商的风险规避系数，以下通过算例来分析。

突发事件下，运用CVaR度量准则来测度制造商所面临的供应风险。供应链的相关参数如成本、市场需求、供应商可靠性、制造商风险规避系数等数值如下：r=5，w=2，c=3，s=1；x服从[50，100]的均匀分布；r服从均值为μ、标准差为σ的正态分布；β∈[0.1，1]；Matlab软件中，β和μ的步长取0.1、σ的步长取0.05。相关参数假设下，主要分析：突发事件风险下的供应链收益共享协调；风险规避系数β、供应商可靠性均值μ、可靠性标准差σ对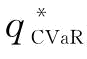的影响。

（1）相关参数假设下，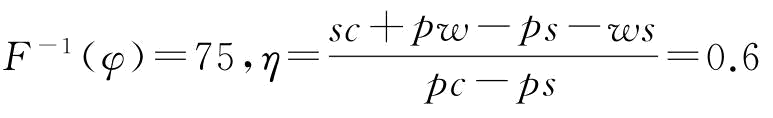

那么，，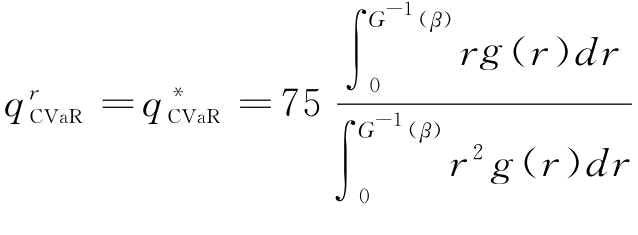

同时，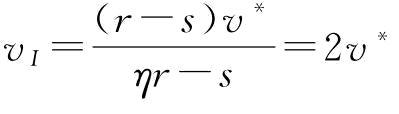

当供应链的最优保留利润设置为分权供应链下制造商的保留利润的2倍时，供应链可以实现收益协调，说明收益共享契约在协调具有突发事件风险的供应链时具有一定的鲁棒性。

（2）令μ=0.6、σ=0.1，β对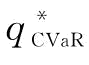的影响如图4-4所示。

可以发现：制造商越是风险规避（β越小），其最优订货量越大，且严格不小于风险中性下的最优订货量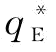（当β=1时，）。

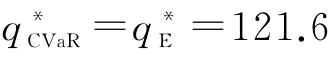（3）保持供应商可靠性标准差σ不变，令σ=0.1，供应商可靠性均值μ和制造商风险规避系数β对制造商最优订货量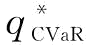的影响如图4-5和表4-1所示。

可以发现：当β保持不变时，μ越小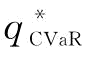，越大，即当供应商的可靠性均值降低时，制造商通过增加订货量来规避风险；当μ不变，β越小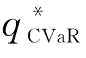，越大，即制造商对突发事件的风险规避程度越高（β越小，风险规避程度越高）；特别地，当β=1时，对应于风险中性情况，此时。

图4-4　制造商风险规避系数对最优订货量的影响

图4-5　供应商可靠性均值和风险规避系数对最优订货量的影响

表4-1　供应商可靠性均值和风险规避系数对最优订货量的影响

（4）保持供应商可靠性均值μ不变，令μ=0.6，供应商可靠性标准差σ对制造商最优订货量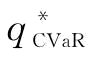的影响如图4-6和表4-2所示。

可以发现：当β=1、β=0.9时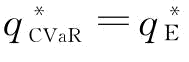，且σ越大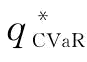，越小；当β=0.8、β=0.7时，σ对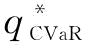的影响并不确定，如表4-2中的加粗数字所示；当β的取值在0.1到0.6之间时，σ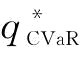越大，越大。

图4-6　供应商可靠性标准差和制造商风险规避系数对最优订货量的影响

表4-2　供应商可靠性标准差和制造商风险规避系数对最优订货量的影响

从（3）和（4）的分析中，我们可以发现：

制造商最优订货量对供应商可靠性均值的敏感性并不依赖于风险规避程度（风险规避系数越小，则说明规避程度越高），且均值对订货量的影响与风险中性的情况是一样的；制造商最优订货量对供应商可靠性标准差的敏感性则依赖于其自身的风险规避程度；当制造商风险规避达到一定程度时，标准差越大，最优订货量越大，这与风险中性的情况是相反的。以上，体现了风险规避型制造商在进行订货时，对供应商可靠性的波动程度较为敏感，当波动程度越大，制造商往往会通过增加订货来规避风险。