本节研究的情形对应于第3章中分析的情景5,即针对的是可控突发事件或一般的风险,即突发事件的性质是可控的,属于常规型突发事件,一般不会造成极端的影响;突发事件的作用对象为制造商的一级供应商;另外,制造商通过双源采购与供应商可靠性改善投资决策来防范风险。
我们研究单一销售季节下的由两个供应商和一个制造商组成的单一产品供应链报童问题,并假设在外在的事件风险下,供应商是不可靠的。由于存在较长的供应前置期,制造商需要在销售季节来临前进行订货决策。相关参数假定如下:
qi:制造商向两个供应商(i=1,2)的订货量。
Qi:供应商的期望发货量或者是制造商的期望到货量。由于供应商是不可靠的,则供应商的期望发货量Qi不大于制造商的订货量qi。
ri是供应商i的可靠性,Gi(.)、gi(.)分别是ri的累积分布函数和概率密度函数,假设ri的概率密度函数是二阶可微的,μi、σi分别代表ri的均值和方差,假设μi≤1、σi≤ui;Qi=μiqi。
X:制造商面临的市场需求,X是随机变量,其概率密度函数和累积分布函数分别为f(.)、F(.)。
p:产品的市场销售价格。
s:产品的残值。
ci:制造商的单位产品采购成本。
不考虑产品的缺货成本,而p>ci>s(i=1,2)是报童模型的一般假设。制造商的目标是在需求不确定下根据供应商的可靠性r=(r1,r2)和成本参数c=(c1,c2)下决定其最优订货数量q=(q1,q2)来最大化自己的利润。
假设π(q1,q2;r1,r2)是制造商的利润函数,Π(q1,q2;r1,r2)是制造商的期望利润函数。为表达方便,用向量表达式π(q,r)和Π(q,r)进行替代。制造商的优化问题可以由下式来表达:
为了便于求解,可以将式(4-1)写成更加紧凑的形式,令φi=(p-ci)/(p-s),则
式(4-2)说明,在保持市场需求和相关成本参数(如产品的销售价格、残值)是外生变量的前期下,制造商的利润取决于供应商的可靠性和采购成本。
双源采购模式下,制造商的供应渠道的选择与订货量的分配直接关系到其期望利润的大小;而制造商的订货量在两个供应渠道间的分配又取决于供应商的可靠性与制造商的采购成本的大小;也就是说,供应商的相关参数决定了制造商的订货偏好。该部分主要研究以下几个问题:
(1)制造商的最优订货量在两个供应商之间是如何分配的,其分配量是如何受到供应商的可靠性和成本组合参数(r1,r2;c1,c2)影响的;特别地,当供应商的相关参数满足什么样的条件下,制造商选择单源采购或双源采购。
(2)在保持采购成本不变的前提下,制造商向一个供应商的订货量是如何受到该供应商和另外一个供应商的可靠性均值与标准差的影响。
(3)供应商不可靠下,制造商应该重点关注的是订货量还是供应商的期望发货量(供应不可靠下,订货量与期望发货量是不相等的;供应商可靠下,订货量与期望发货量是相等的)。
(4)制造商向一个供应商的期望实现订货量又是如何受到该供应商和另外一个供应商可靠性均值、标准差及其联合影响的。
(5)供应商可靠性是如何影响制造商的最优期望利润的。
我们首先运用随机占优理论(Stochastic Dominance)对供应商可靠性进行界定。假设ξ1和ξ2是两个随机变量,其分布函数分布为G1和G2。
引理1:对于任何t,假设G1(t)≤G1(t),则ξ1一阶随机占优于ξ2,记为ξ1≥1ξ2;对于任何x,假设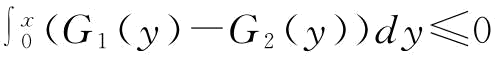 ,则ξ1二阶随机占优于ξ2,记为ξ1≥2ξ2。
,则ξ1二阶随机占优于ξ2,记为ξ1≥2ξ2。
对于供应商可靠性因子r1和r2,假设r1≥r2,说明供应商1比供应商2具有更高的可靠性;也就是说,在某一个确定的时间内,更可靠的供应商将会产生一个随机大的产品数量来满足市场需求,即有E[r1]≥E[r2]。对于供应商可靠性因子r1和r2,假设r1≥2r2,说明相比较供应商2来说,供应商1的可靠性变异性更小;当E[r1]=E[r2],r1≥2r2意味着σ[r1]≤σ[r2]。引言1说明,供应商的可靠性大小不仅取决于其均值的大小,还取决于其标准差的大小;保持标准值不变,均值越大,可靠性越高;保持均值不变,标准差越小,可靠性越高。那么,如何表达供应商可靠性的均值与标准差对供应商的可靠性的联合影响,以下定义供应商可靠性变异系数,其意义在于研究供应商可靠性对制造商订货决策的影响。
定义1:定义γk=σk/uk为供应商k的可靠性变异系数,若γi<γj,相比较供应商j而言,供应商i具有更高的可靠性或更好的稳定性(1)。
我们首先研究制造商的最优订货量及其在两个供应商之间的分配,有如下结论:
命题1:存在一个最优的订货向量 使得▽qi(j)Π(q*,r)=0,即最大化制造商的期望利润;当需求X服从[a,b]的均匀分布时,制造商向两个供应商的最优订货量为:
使得▽qi(j)Π(q*,r)=0,即最大化制造商的期望利润;当需求X服从[a,b]的均匀分布时,制造商向两个供应商的最优订货量为:
其中,F-1(φi(j))=a+(b-a)φi(j),γi(j)=σi(j)/μi(j),i,j=1,2
证明:式(4-2)分别对qi进行一阶求导和二阶求导得:
所以,Π(q,r)为凹函数。
令▽qiΠ(q,r)=0,则[a+φi(b-a)]Er(ri)=F-1(φi)Er(ri)=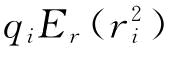 +qjEr(rirj),可以求出
+qjEr(rirj),可以求出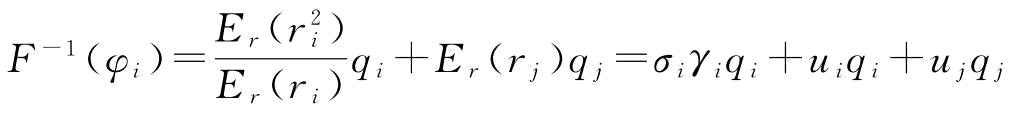 ;
;
同理,F-1(φj)=σjγjqj+uiqi+ujqj;联立求解F-1(φi)、F-1(φj)表达式,可以推导出式(4-3)。
从结论1可看出,制造商的供应渠道的选择与订货量的分配是由两个供应商本身的可靠性与成本的组合参数来决定的,以下分析制造商选择单源采购或双源采购所需要满足的条件。
推论1:制造商选择单源采购还是双源采购,主要取决于两个供应商的成本与可靠性参数满足的条件,即当满足以下条件时
证明:很明显,式(4-3)中可以看出:当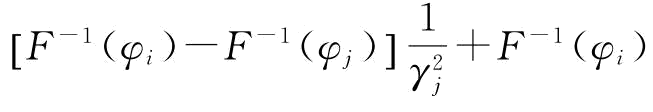 0时,制造商选择向供应商j单源采购;反之,制造商选择双源采购。
0时,制造商选择向供应商j单源采购;反之,制造商选择双源采购。
推论1中,γi的表达式的右边表示调整后的供应商i和j间的成本差异,即当供应商i的可靠性的优势能弥补其在成本上的劣势后,制造商选择向其单源采购,也就是供应商i能够获得制造商的全部订单;反之,制造商选择双源采购。
推论2:在保持供应商的成本参数相同(ci=cj)的情况下,制造商向一个供应商i的最优订货量qi随着该供应商的可靠性均值和可靠性标准差的增加而减小,随着另外一个供应商j的可靠性均值的降低和标准差的增加而增大。(https://www.xing528.com)
证明:当供应商的成本参数相同时,可以将式(4-3)改写成式(4-5),得到相关结论。
分析供应商的可靠性对制造商的订货分配决策中,发现一个有意思的现象:制造商向一个供应商的最优订货量随着另外一个供应商的可靠性的降低而增大,但是与该供应商自身的可靠性的高低关系并不确定,这一点与Burke et al与Dada et al的分析是不同的。Burke et al指出:制造商向一个供应商的最优订货量是该供应商可靠性均值的增函数,是该供应商可靠性标准差的减函数。在保持供应商成本相同情况下,从式(4-5)可以看出:当供应i的可靠性均值增加时,制造商向其最优订货量反而减少,即供应商i的可靠性均值与可靠性标准差对其订货量的影响是同向的,所以制造商向一个供应商的最优订货量对该供应商的可靠性的敏感性难以确定。
Dada et al指出:相比可靠的供应商来说,不可靠的供应商往往会使得报童订货量增加,这是与常理相符的,因为在供应不可靠下,如果供应链下游企业能观察到供应商的可靠性,其可以加大订货量来实现自身的订货目标。而Dada et al定义的可靠性是可靠性的均值,所以并没有考虑到供应商可靠性的标准差。从式(4-5)中可看出,供应商可靠性的标准差越大,说明其越不可靠,而下游企业的订货量越小,这又与他的结论是不相符的。综合以上,Burke et al在分析供应商可靠性对制造商最优订货量的敏感性分析时,存在一定的问题;另外,与Dada et al相比,我们所用到的随机产出模型是不一样的,这也导致了结论的不同。
以上对制造商的订货决策进行了研究,重点分析供应商成本与可靠性对制造商订货决策的影响,这一点Burke et al和Dada et al也进行了类似的研究。但实际上,在面对供应商不可靠的风险时,供应链下游企业应该重点关注期望发货量而不是订货量;而在供应商可靠下,供应链下游企业的订货量与供应商的期望发货量是相等的。供应商不可靠下,供应商的期望发货量、两个供应商总的期望发货量以及制造商的期望利润函数的表达式,如式(4-6)、式(4-7)和式(4-8)所示。
以下,研究在面临供应商不可靠的风险下,制造商对供应商的偏好问题以及有关供应商的期望发货量以及制造商的期望利润对供应商可靠性变异系数的敏感性问题。
定义2:供应商的可靠性变异系数和成本组合参数(γi,γj;ci,cj)下,若供应商的期望发货量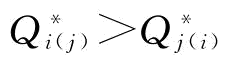 ,则表明制造商偏好供应商i(j)。
,则表明制造商偏好供应商i(j)。
推论3:当供应商i(j)的可靠性变异系数满足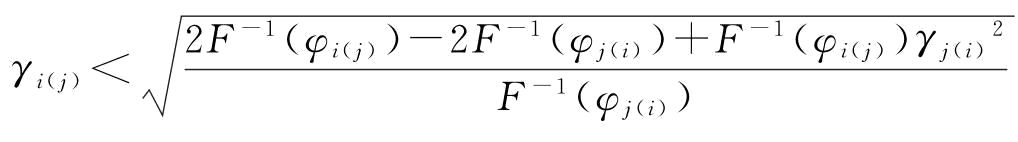 时,制造商偏好供应商i(j);特别地,当
时,制造商偏好供应商i(j);特别地,当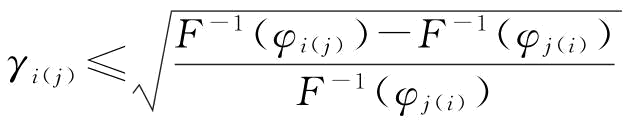 时制造商完全偏好于供应商i(j),即向供应商i(j)单源采购。
时制造商完全偏好于供应商i(j),即向供应商i(j)单源采购。
证明:假设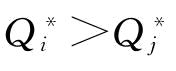 ,由式(4-6)得:
,由式(4-6)得:
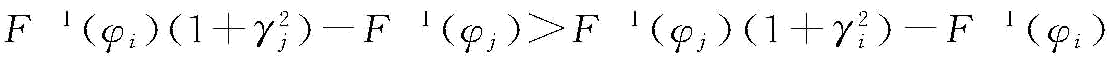 ,即可得到上面结论;
,即可得到上面结论;
特别地,当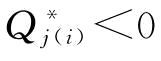 ,制造商向供应商i(j)单源采购,具体证明见推论1。
,制造商向供应商i(j)单源采购,具体证明见推论1。
推论4:(1)在保持供应商的成本参数相同(ci=cj)的情况下,供应商i的期望发货量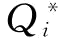 是其可靠性变异系数γi的增函数,是另外一个供应商j的可靠性变异系数γj的减函数;
是其可靠性变异系数γi的增函数,是另外一个供应商j的可靠性变异系数γj的减函数;
(2)总的期望发货量Q*是供应商可靠性变异系数γi(j)的减函数;
(3)制造商期望利润是供应商可靠性变异系数γi(j)的减函数。
证明:(1)当ci=cj,那么,F-1(φi)=F-1(φj);
则可以将式(4-6)改写成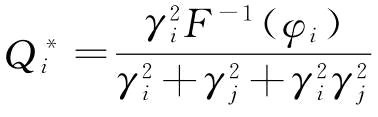 ;很明显,γi越小,γj越大,则
;很明显,γi越小,γj越大,则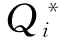 越小;
越小;
(2)从式(4-7)可以看出,γi(j)越小,Q*越大;
(3)Π(Q*)对γi一阶求导得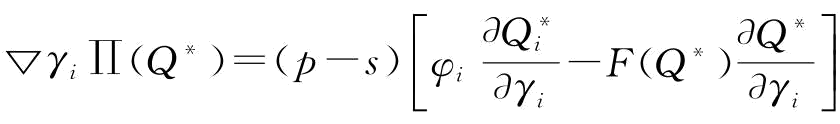 ,以下证明▽γiΠ(Q*)<0,只需证明φi>F(Q*)
,以下证明▽γiΠ(Q*)<0,只需证明φi>F(Q*)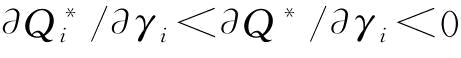 。将式(4-4)改写成▽qiΠ(q,r)=(p-s)[φiEr(ri)-Er(riF(riqi+riqi))]≥0,由期望函数的性质,可知:Er[riF(riqi+rjqj)]≥Er(ri)Er[F(riqi+rjqj)],则φi≥ErF(riqi+rjqj),即有φi≥F(Q*)。式(4-6)减式(4-7)并对γi一阶求导得:
。将式(4-4)改写成▽qiΠ(q,r)=(p-s)[φiEr(ri)-Er(riF(riqi+riqi))]≥0,由期望函数的性质,可知:Er[riF(riqi+rjqj)]≥Er(ri)Er[F(riqi+rjqj)],则φi≥ErF(riqi+rjqj),即有φi≥F(Q*)。式(4-6)减式(4-7)并对γi一阶求导得:
其中,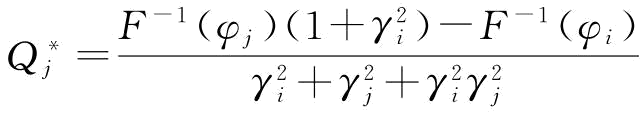 ;
;
综述以上,▽γiΠ(Q*)<0,即供应商可靠性的变异系数越小,制造商的期望利润越大。
推论4说明了提升和改善供应商可靠性对下游企业来说是具有一定价值的,但同时也要考虑改善投资成本与收益之间的权衡。企业可以通过专业保险公司对供应商所处的环境进行风险评估找出脆弱环节,再确定可靠性改善的途径和措施。该部分主要研究对供应商的可靠稳定性进行改善的价值。为方便直观表达,假设制造商选择一个供应商i进行可靠性改善,比如为防止地震、火灾等灾害对供应商生产运营系统的破坏,可考虑对供应商生产工厂建筑物维护结构进行加固、对供应商生产设施进行防火保护如安装自动喷淋防火系统等,来增加运营设施抗突发事件的能力,增强运营设施及系统的可靠性。假设在制造商的改善努力水平为ti、单位努力成本为mi下,供应商可靠性变异系数以概率θi改降低到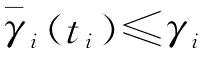 ,以概率1-θi保持原来的γi不变;其中,
,以概率1-θi保持原来的γi不变;其中,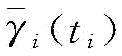 是改善后的供应商可靠性变异系数,是制造商改善努力水平ti的函数(一般情况而言,
是改善后的供应商可靠性变异系数,是制造商改善努力水平ti的函数(一般情况而言,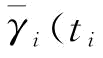 )是ti的非递增函数)。制造商的决策流程为:先进行可靠性改善投资miti,在观察到可靠稳定性的改善水平后,进行订货决策。这实际上是一个两阶段随机规划问题,即第二阶段进行订货决策,第一阶段进行可靠性改善投资。令制造商的第二阶段期望利润函数为
)是ti的非递增函数)。制造商的决策流程为:先进行可靠性改善投资miti,在观察到可靠稳定性的改善水平后,进行订货决策。这实际上是一个两阶段随机规划问题,即第二阶段进行订货决策,第一阶段进行可靠性改善投资。令制造商的第二阶段期望利润函数为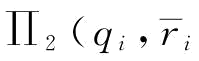 ),第一阶段期望利润函数为
),第一阶段期望利润函数为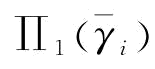 ,则有:
,则有:
其中,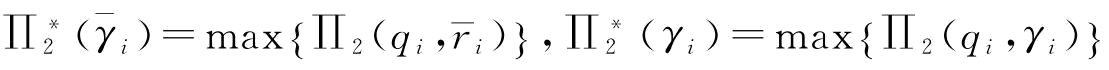 。对于制造商来说,其决策主要是基于可靠性改善能否带来一定的价值,令ΔΠ=
。对于制造商来说,其决策主要是基于可靠性改善能否带来一定的价值,令ΔΠ= ,即制造商进行供应商可靠性改善前后的利润之差。以下对制造商的订货与改善投资决策进行分析。
,即制造商进行供应商可靠性改善前后的利润之差。以下对制造商的订货与改善投资决策进行分析。
命题2:在制造商愿意进行供应商可靠性改善下,供应商的期望发货量为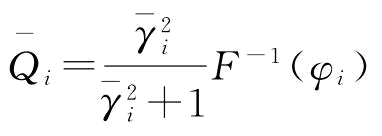
证明:对式(4-9)进行优化即可得到相关结论,具体可以参照命题1的证明。
命题2中可发现:在制造商愿意对供应商可靠性进行改善的前提下,供应商期望发货量增大,这就是制造商关注供应商可靠性改善的价值所在。因为,在单源采购中,可靠性改善前供应商的期望实现订货量为 ,而
,而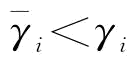 ,所以
,所以 。那么,制造商所需投入的改善投资成本满足什么条件,其决策能达到最优?
。那么,制造商所需投入的改善投资成本满足什么条件,其决策能达到最优?
命题3:供应商可靠性变异系数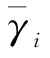 和改善投资成本
和改善投资成本 满足以下条件时,制造商愿意对供应商可靠性进行改善
满足以下条件时,制造商愿意对供应商可靠性进行改善
证明:当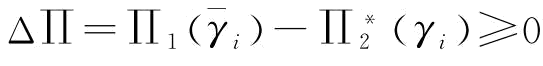 ,可靠性改善才有意义,将式(4-10)代入得:
,可靠性改善才有意义,将式(4-10)代入得: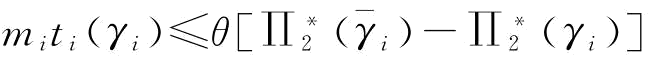 ,上式两边对
,上式两边对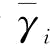 求导得
求导得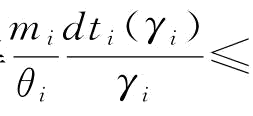
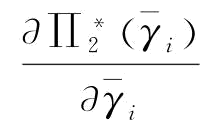 ,进一步求解可以得到式(4-11)的结果。
,进一步求解可以得到式(4-11)的结果。
以上说明可靠稳定性改善投资成本不能大于改善成功概率下所带来的收益,否则失去改善的意义;同时,也说明可靠性稳定性改善的投资水平不能大于某一个特定的值,因为可靠稳定性的提升是需要成本投入的,这与常理是吻合的。
推论5:制造商最优改善努力ti是:
(1)改善成本mi的减函数;
(2)改善成功概率θi的增函数;
(3)市场需求X的增函数。
证明:由式(4-11)可以很明显得到推论4的相关结论。
推论5说明零售愿意投入的改善努力与改善投资成本、改善成功的概率和市场需求是密切相关的。改善成本太高,企业的改善意愿就会降低,因为要考虑投资成本与收益的权衡。改善的成功的概率是与企业自身对风险发生的类型与强度的判断的准确与否是相关的,何种风险事件会发生以及发生在供应商生产运营的哪个环节也是非常难以掌控的,所以即使进行改善投资也并不能保证风险不会发生。另外,如果企业所处于的市场是成长性的,即市场需求量持续增大,那么,制造商改善投资的意愿会有所增强,愿意投入成本来规避相应的风险。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




