湖北省现代服务业就业弹性系数测算方法与应用

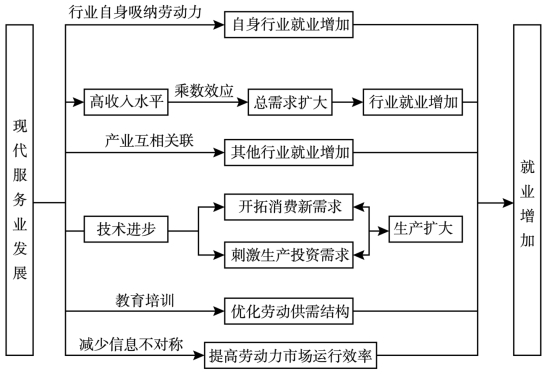
图6-1　现代服务业促进就业增长路径

本研究的工具有2个，就业弹性和结构偏离度。本研究的研究思路是，利用回归模型实证测算湖北省现代服务业的就业弹性系数和其中各个细分行业的就业弹性系数，再利用差分方法测量不同年份中的湖北省现代服务业的就业弹性系数。通过这两种手段实现对湖北省现代服务业就业的影响因素侦测。

（1）就业弹性。

在研究产业经济发展与就业之间的相关关系时，主要使用的工具是就业弹性。

就业弹性是指就业增长率比上经济增长率的数值，它代表着经济增长率变动1%时，就业增长率变动的百分比值，即：就业弹性系数＝就业增长率/产值增长率。在正常的情形下，就业弹性系数一般处于0 和1 之间，影响该系数的因素主要有经济体结构和劳动力成本等。劳动力的就业成本主要由就业所需的资本数量和劳动力成本构成，假如劳动密集型企业、组织在社会经济系统中占据较高比例，就业成本会相对较低，就业弹性则相应更高。维持较高的就业弹性对于经济系统内部的就业具有重要的意义。

就业弹性的计算方法有两种：第一种是用回归模型来完成，第二种是利用差分方法来完成。

在借鉴中科院国情分析小组的研究成果的基础上，本章采用回归模型来完成。该模型认为经济增长与就业量之间是非线性关系，用公式描述为如下形式：

其中，L 为某一产业的就业人数，Y 为对应的经济产值，A 为常数项，α为就业弹性系数。

对公式（6-1）两边取对数进行简化，得到如下形式：

对公式（6-2）进行差分处理，得到公式（6-3）：(www.xing528.com)

其中，μ 为就业弹性系数，L 为某一产业就业人数，ΔL 为就业人数的变化量，ΔL/L 为就业人数增长率，Y 为经济产值，ΔY 为经济产值的增加量，ΔY/Y 为经济产值增加率。

公式（6-3）中，当μ＜0 时，表示经济产值的增加会抑制就业数量的增加；当μ＞0 时，表示经济产值的增加会促进相应就业人数增多，μ的数值越大，就代表着就业量会因经济增长率的增加而大幅增加，产业的发展对于就业的帮助也就越明显，存贮劳动力的数量也会更多，相反该作用越不明显。

（2）产业结构偏离度。

产业结构偏离度指各产业增加值的比重与相应的劳动力比重的差异程度。国民经济系统三类产业的生产率不尽相同，某一类产业的产值结构与相应的就业结构不均衡的现象就是产业结构的偏离度，即某一产业总量占GDP 的比例与该产业就业人数占总就业人数的比例不相等。

在新古典经济学的收入分配理论中，劳动要素所得取决于对应的劳动生产率。在完全竞争经济环境下，劳动要素可获取的收入等于劳动力的边际劳动生产力，这也就意味着如果国民经济系统中的三类产业相互连通，产业之间不存在阻碍劳动力流动的阻力，劳动力会选择使自身收益最大化的产业就业，长此以往三类产业间的收入水平在供求关系的作用下会趋于一致，也就是理论中的三类产业最终的劳动生产率会逐渐趋同，产业结构偏离度趋向于零。这个结论已经得到过一些经济学家的实证验证，并被总结成了产业发展与演进的国际标准模式，如表6-1 所示。

表6-1　产业结构偏离度演进的理论模式

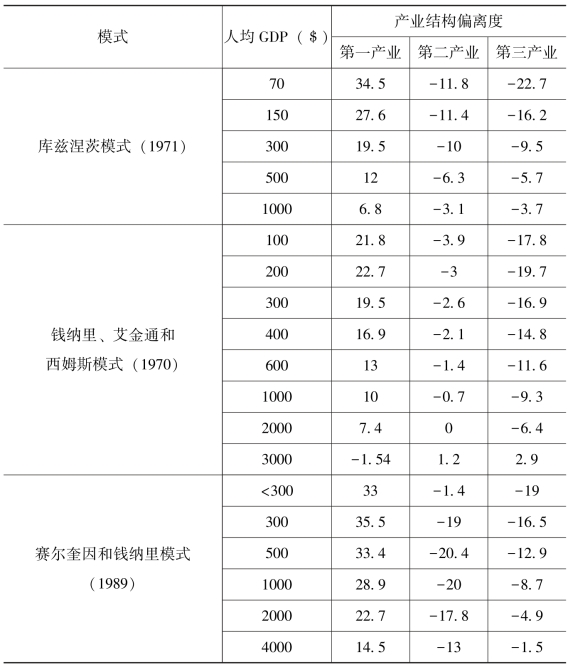
从表6-1 可以看出，随着人均GDP 的增长，就业结构与三大产业产出结构的产业结构的偏差程度将逐渐降低，直至波动到0 左右。d＜0时，代表产业的劳动力吸纳状态比较饱和；d＞0 时，代表产业有空间继续吸纳劳动力。

产业结构偏离度用如下公式计算：

其中，D 为产业结构偏离度，Y 为某一产业产值，V 为GDP 总量，Y/V为相应产业的产值占比，L 为就业人数，N 为总就业人数，L/N 为该产业的就业人数占比。