(1)验证数据是否适合进行因子分析。通过对原始数据的标准化处理和KMO及Bartlett’s球型检验(如表17-2所示),可认为变量间相关性较强,各变量间不相互独立,可以进行因子分析。
表17-2 KMO检验与Bartlett’s球形检验

(2)运用SAS9.3计算数据标准化后的样本相关阵的特征值、贡献率,如表17-3所示。由表17-3可知,若取公因子的个数m=4,则其特征值基本大于或接近于1,且累计贡献率已达到90%以上(0.9124),即说明前4个公共因子已经足够反映出原始变量的大部分信息。图17-1中的陡坡图也可以看出前面四个的因子特征值变化非常突出,从第5个开始累计方差解释趋于平缓,这也与表17-3吻合。
表17-3 相关阵的特征值、贡献率和累计贡献率


图17-1 公共因子陡坡图
(3)根据确定的公因子个数m=4计算出初始的因子载荷矩阵,为了更好地对因子进行解释,对初始因子载荷矩阵进行方差最大的正交旋转,如表17-4所示。从旋转后的因子载荷矩阵中可以看出第一个公因子在变量X1、X2、X5、X6、X7、X10、X13、X14、X15上的载荷都比较大,分别是工业总产值、应缴增值税、利润总额、市场占有率、出口交货值、资产总计、专利申请数、新产品开发项目数、新产品销售收入。该因子反映了上述9个变量的整体信息,这些变量无一例外都展现了产业规模的情况。规模越大,相应地这7个指标也会越大。所以,第一个公共因子可以命名为市场规模因子。第二个公因子在指标X3、X8上的载荷较大,分别是成本费用利润率、销售利润率。这些指标都可以反映企业在市场经营活动中的相关竞争力大小,这些指标越大,企业的经营状况越好,企业抵抗市场风险的能力越强,因而可将此公共因子命名为经营因子。第三个公因子在指标X4、X9上的载荷较大,分别是劳动生产率、生产销售比率。企业通过不断创新,改进技术,提高劳动生产率,研发出的新产品也会更受到市场的欢迎,生产的产品也会更易卖出,此公共因子在某种程度上反映了企业创新所带来的成果,因而可将此公共因子命名为创新结果因子。第四个公因子在指标X11、X12上的载荷较大,分别是企业平均资产总额、亏损企业占比。企业平均资产越高代表企业的平均规模就越大,亏损企业占比越低代表这一地区企业的整体实力就越强,这两个指标共同反映了某一地区企业的基础规模实力,因而可将此公共因子命名为基础规模因子。
为了更好地了解各地区在每个公共因子上的发展情况,需要计算出各地区在各个公共因子上的得分情况。使用SAS软件中的FACTOR过程进行因子分析并输出因子得分系数矩阵,如表17-4所示,由此可得到因子得分函数,并以各公因子的信息贡献率作为权重计算出各地区的综合得分。
表17-4 因子载荷矩阵和因子得分系数矩阵
 (https://www.xing528.com)
(https://www.xing528.com)

(4)将标准化后的原始数据代入式(17-7)、(17-8)、(17-9)、(17-10)和(17-11),可计算出2010—2014年各地区的因子具体得分情况及排名,如表17-5和表17-6所示。
表17-5 2010—2014年我国各省区市因子得分情况

表17-6 2014年各省区市公共因子得分情况及排名

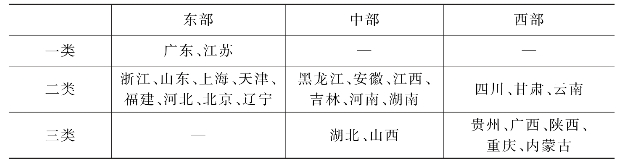
(5)将各年份的因子得分值作为TOPSIS模型的变量代入公式进行计算,可得出各省区市电子信息产业综合竞争力的相对贴近度,如表17-7所示,贴近度越接近于1表示竞争力越强。为了更清晰地反映我国东中西部电子信息产业的竞争力情况,以贴近度0.5及0.2为分界线将全国各省区市电子信息产业竞争力分为三类,结果如表17-8所示。可见,广东、江苏较强,湖北、山西、贵州、广西、陕西、重庆、内蒙古较弱,其他省区市处于中间;总体上,东部地区电子信息产业竞争力较强,中部地区次之,西部地区较弱。
表17-7 各省区市2010—2014年基于因子分析的TOPSIS法评价结果

表17-8 东中西部电子信息产业竞争力聚类结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




