工业生产变量的度量方法及地区人力资本衡量方法

1.被解释变量

本文的被解释变量是全要素生产率（TFP），这个变量的计算比较繁琐，需要通过以下步骤：第一，确定测算TFP的方法。索罗剩余法测算TFP将会导致技术计量问题，即同时性偏差（Simultaneity Bias）和样本选择问题（Selectivity and Attrition Bias）。Olley和Pakes（1996）基于一致半参数估计方法提出了OP方法，该方法使用一个生存概率来估计企业的生存和退出，因此该方法主要适用于估计企业层面的生产率。Levinsohn和Petrin（2003）提出的测算生产率的LP方法涉及中间投入，尽管中间投入比OP方法更容易获得，但是由于本文来使用产业层面的数据，只能计算出2000—2007年的中间投入，所以也无法使用该方法。与同样可以测定决策单元的全要素生产率的数据包络分析方法（Data Envelopment Analysis，DEA）相比，随机前沿分析方法（Stochastic Frontier Analysis，SFA）的优势是可以使用计量方法对前沿生产函数进行估计，并能够对估计出的参数进行统计检验，具有更为可靠的经济理论基础；通过从复合误差中有效分离技术非效率与随机误差的方法，人们可以进一步考察导致效率差异的背后因素（Kumbhakar and Lovell，2000），所以本文采用SFA方法来测算TFP。

第二，确定生产函数形式。本文借鉴Kumbhakar和Lovell（2000）的随机前沿模型的一般形式：

其中，i表示行业，t表示时间，y表示产出，xit表示投入变量。误差项vit-uit 为复合结构；N（0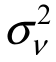，），表示一般测量误差或一般不可控的随机因素的影响；uit技术非效率项，且与vit相互独立，表示个体冲击的影响，根据Battese和Coelli（1995）的设定，uit服从非负断尾正态分布，即uit服从，且有式（33）：

式（33）中，itη是决定技术无效率随时间变化的函数，待估参数η表示技术效率指数的变化率。η＞0表示随着时间的推移，相对前沿的技术效率不断改善；η＜0表示技术效率不断恶化；η=0表示技术效率不随时间变化。

Battese和Coelli（1992）设定了方差参数，其中，来检验复合扰动项中技术无效率项所占的比例，λ介于0与1之间。若λ=0被接受，表明实际产出与最大产出之间的距离均来自于不可控的纯随机因素，此时无需采用SFA方法，直接运用OLS方法即可。

本文采用面板数据进行实证检验，随着时间的推移，由于不能事先确定技术是否为中性，产出弹性是否固定，因此在生产函数形式的选择上，本文选用超越对数生产函数形式的随机前沿模型。假定有一种产出（Y），两种投入资本（K）和劳动（L），并且引入要素投入和时间趋势t的交互项，将随机前沿模型的一般形式（34）具体化并取对数得：

第三，确定投入产出变量。（1）产出变量（Y）采用工业实际增加值，将工业增加值用以2000年为基年的出厂价格指数平减得到。（2）投入变量是资本（K）和劳动（L）。借鉴孙早和宋炜（2013）的研究，资本投入采用固定资产实际净值年平均余额衡量。劳动投入采用全部从业人员年平均人数衡量。

第四，估计出生产函数和计算TFP。表1报告了工业分行业随机前沿生产函数的估计结果。模型1和模型2分别是投入产出变量按照从业人数、主营业务收入调整到全部工业口径的估计结果。模型1和模型2中η的估计p值大于0.1，均不显著，所以本文选择技术效率不随时间而变的随机前沿模型。本文没有报告技术效率随时间变动的随机前沿模型的参数估计结果，而只报告其中的η的估计值。从模型1和模型2的Log likelihood、Waldχ2（9）的统计量看，模型回归的整体效果非常好，都具有很强的解释力，同时资本、劳动的平方项及交互项的系数符合经济理论预期。模型1和模型2的γ的值分别是0.89和0.94，表明效率的偏差主要来源于非技术效率，并且mu在1%的显著水平上不等于0，说明本文使用SFA方法估计生产函数是合理的。

表1　分行业随机前沿生产函数估计结果

注：括号内的数值为z统计量，***、*分别表示在1%、10%的水平上显著。(www.xing528.com)

得到参数估计后，本文借鉴Fuentes等（2001）在SFA框架下提出的式（35）来测算TFP：

在式（35）中，TEit为各细分行业的技术效率。

2.解释变量

第一，一般人力资本（OH）和专业人力资本（PH）。刘榆、刘忠璐和周杰峰（2015）使用专科及以下受教育程度的就业人数来衡量地区层面的一般人力资本，使用本科及以上受教育程度的就业人数来衡量地区层面的专业人力资本。本文使用工业分行业层面的数据，所以仿照吴延兵（2012）的做法，使用分行业的研发（R&D）人员全时当量来衡量专业人力资本，用分行业从业人数减去R&D人员全时当量得到生产人员数，即一般人力资本。

第二，企业家人力资本（EH）。企业家人力资本不能使用受教育程度来衡量，不少企业家的科学文化水平相对不高，但其创办的企业经营得也很成功，因此受教育程度不能全面反映企业家人力资本的特点和水平（张小蒂和姚瑶，2011）。Beugelsdijk 和Noorderhaven（2004）使用自我雇用率作为企业家精神（人力资本）的代理指标，Glaeser和Kerr（2009）采用历年新增私营企业数量来度量企业家精神（企业家人力资本），张小蒂和姚瑶（2011）为了揭示中国民营企业家的成长特征，采用地区每万人口中民营企业的数量来衡量企业家人力资本。刘榆、刘忠璐和周杰峰（2015）采用每万人口中企业法人单位数来测度企业家人力资本。改革开放以来，民营经济的发展速度成倍高于全国整体经济增长速度，民营经济已经成为我国国民经济的重要组成部分，扩大就业的主要渠道、国家税收的重要来源、促进对外贸易的有生力量，民营企业家更是民营企业的灵魂。考虑到企业家人力资本内涵的相对重要性及数据的可得性，本文借鉴张小蒂和姚瑶（2011）的做法，采用分行业规模以上工业民营企业中每万从业人员中民营企业的法人单位数来作为企业家人力资本的代理变量。

3.控制变量

（1）行业国有产权比重（OWN）。本文采用国有及国有控股企业从业人员年平均从业人数的比重（分行业国有及国有控股企业从业人员平均人数除以该分行业内全部企业从业平均人数）度量工业分行业的国有产权比重。（2）行业内平均企业规模（SIZE）。本文采用行业内平均每个企业的资本存量（分行业的固定资本存量除以行业内企业单位数）行业内平均企业规模。（3）政府科研补贴强度（TTBTQ）。本文采用政府科研补贴占研发资本支出的比重来衡量。（4）自主研发强度（RDQ）。本文采用研发资本支出与主营业务收入的比重来衡量。（5）总资产贡献率（ZGX）。参考孙早和宋炜（2012）的研究，本文采用利税总额与利息支出之和占资产总计的比重来表征。（6）外部融资依存度（RZD）。根据Brewer（1993）的做法，本文采用长期负债除以固定资产原价来表示。（7）对外技术依存度（JSD）。本文借鉴孙早和宋炜（2014）的研究，采用国外技术引进支出占技术改造经费、国外技术引进支出、消化吸收经费支出、购买国内技术经费支出总额的比重来衡量。（8）资产负债率（FZL）。本文采用负债总计除以资产总计来衡量。

表2和表3分别给出了变量的设置与说明及主要变量的描述性统计。

表2　变量的设置与说明（j=1）

表3　主要变量的描述性统计（j=1）