比较衡量投资方案的决策风险，需要借助三个统计量：期望值、标准差及变差系数。下面通过例子来具体说明。
例8.2 假定有两个投资方案，二者的初始投资相同。甲方案是投资矿产开发，根据地质部门预测找到有开采价值矿藏的概率为0.6，找不到的概率为0.4，找到的话每年可获利1 000万元，找不到则损失1 000万元。乙方案是投资办厂，预测市场销路好的概率为0.8，获利为220万元，市场销路一般的概率为0.2，获利为120万元。从甲、乙方案的收益期望值来判断：
甲方案：1 000×0.6+（-1 000）×0.4=200（万元）
乙方案：220×0.8+120×0.2=200（万元）
所以，甲、乙两个方案的期望值相等，但是两个方案的风险并不完全相等，甲方案收益的可能性在（1 000万元，-1 000万元）二者中出现，而乙方案收益的可能性是在（220万元，120万元）二者中出现。显然，两个方案虽然期望收益相等，但后者的风险小得多。
投资方案各种可能结果的规律分布的分散程度可以通过求标准差σ来测定，σ越大说明风险越大。标准差σ的计算公式如下：
式中：σ表示标准差；Ri表示第i种结果的现金流量；R表示现金流量的期望值；Pi表示发生第i种结果的概率。
在例8.2中：
甲方案：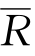
=200万元，R1=1 000万元，P1=0.6，R2=-1 000万元，P2=0.4。(www.xing528.com)
乙方案：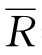
=200万元，R1=220万元，P1=0.8，R2=120万元，P2=0.2。
很明显，σ乙＜σ甲，所以乙方案风险相对较小。
如果直接用风险大小作为决策依据，那么，期望值相同时，取标准差较小的方案，风险就较小。如果期望值不同，则要用变差系数来测定它们的相对风险，变差系数大说明方案的风险大。变差系数的计算公式为：
式中：v表示变差系数；σ为标准差；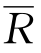
为现金流量的期望值。
例8.3 假定某企业有两个投资方案，甲方案的期望现金流量为100万元，标准差为1 000元；乙方案的期望现金流量为20万元，标准差为500元。问哪个方案的风险较大？
解：甲方案的变差系数
乙方案的变差系数
很明显，v乙＞v甲，所以乙方案的风险比甲方案的风险要大。
总之，任何投资决策都可能或多或少地存在着一定的风险，风险的大小往往各不相同。在进行决策时，通常需要综合考虑和权衡各个方案的相对风险和报酬。在多数情况下，对方案的选择是通过使用经过风险调整后的贴现率来计算和比较而得到的。其方法是在计算每个方案的净现值时，依据它们各自相对风险的大小估算风险补偿率来提高其贴现率。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
