国际陆港空间布局中的模糊C-均值聚类法应用

1.模糊C-均值聚类法及其原理

模糊C-均值聚类算法(Fuzzy C-Means，FCM)是一种经典的模糊聚类算法。FCM算法首先是由E.Ruspini提出来的，后来J.C.Dunn与J.C.Bezdek将其推广成模糊聚类算法。FCM算法是基于对目标函数优化的一种数据聚类方法。聚类结果是每一个数据点对聚类中心的隶属程度，该隶属程度用一个数值来表示。FCM算法是目前广泛应用的一种基于划分的聚类方法，原理是使被划分到同一簇的对象之间相似度最大，而不同簇之间的相似度最小。

设聚类目标是s维实数空间Rs的一个有限样本空间数据集，数据集的元素个数为n。当FCM算法把样本数据聚为c个模糊类，设ci为每一个类i的聚类中心，dij=‖ci-xj‖为第i个聚类中心与第j个数据点间的欧几里得距离，加权指数m ∈[1，∞)。在模糊划分中，每一个元素不能严格地被划分到某一类，而是以一定的隶属度属于某一类。令uij表示第j个元素属于第i类的隶属度，隶属度U={uij}是一个n×c维矩阵，

则模糊C-均值聚类的目标函数为：

模糊C-均值聚类的思想是迭代uij与ci，使目标函数最小。具体步骤如下：

(1)给出分类数c和加权指数m。

分类数c值一般根据模糊聚类有效性函数Sxb确定。

先给定c的范围[2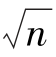，]，计算当2≤c≤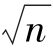时，每个整数c对应的Sxb值，比较各Sxb值，Sxb值最小时对应的c值即为所求，即聚成c类时，用这种方法所获得的聚类效果最好。

(2)在区间[0，1]上随机初始化隶属矩阵U，使其满足约束条件

(3)计算c个聚类中心ci，i=1，2，…，c。

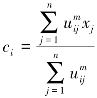
其中，mindwij为第i个聚类中心和第j个聚类中心之间距离的最小值。

(4)计算目标函数J，如果它相对于上次目标函数的改变量小于某个确定的阈值ε，则迭代停止。

(5)计算新的U矩阵，然后返回第(2)步。

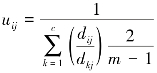
2.基于模糊C-均值聚类的国际陆港空间布局聚类分析(www.xing528.com)

(1)聚类指标的选择。

根据本章6.2节的分析，本书采用的模糊C-均值聚类指标为GDP、GDP增长率、进出口总额、进出口总额增长率、工业总产值、等级公路密度、批发零售业销售总额、货运量、交通区位和外商投资总额十个指标。

(2)数据标准化。

由于指标间极差不一样，且有负值，本书采用平移-极差变换对原始数据进行标准化。

(3)根据聚类有效性函数，确定分类数c和加权指数m。加权指数取经验值m一般为1.5～2.5，一般情况下都取2，本书取m=2。通过式(6.2)得c=4。

(4)得到最终隶属度矩阵U。

(5)聚类结果。

根据最终隶属度矩阵U，得到最终聚类结果如表6.5所示。

3.聚类有效性评价

根据表6.5模糊聚类的结果，运用式(6.1)计算其F统计量得：

F模糊C-均值聚类=43.450 7

查F分布表得：

F0.05(4-1，147-4)=F0.05(3，143)=2.6

由于F模糊C-均值聚类＞F0.05(3，143)，根据数理统计方差分析理论可知，运用模糊C-均值聚类法将样本分为四类比较合理。

表6.5　模糊C-均值聚类结果

续表