1.系统聚类法及其原理
聚类分析是对事情进行分类的一种多元统计方法。分类问题在科学研究、社会生活中广泛存在。聚类分析中的系统聚类法研究的对象是大量的样品,要求能合理地对所有样品进行分类。由于同类事物具有很强的相似性,即同类事物之间的距离应较小,因此可用距离统计量作为分类依据。
用系统聚类法解决实际问题时,把每个分类对象称为样品,并根据对象的性质选择若干指标(特征变量),得到每个样品的所有指标值。由每个样品的所有指标值组成一个数据矩阵,这个样本信息矩阵是系统聚类分析的基础。论域X={x1,x2,…,xn}为样本空间,该样本信息矩阵为:
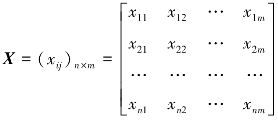
其中,n为样品数,m为特征变量数。
第i个样品的观测值:(xi1,xi2,…,xim)T,i=1,2,…,n。
第j个指标的观测值:(xj1,xj2,…,xjm)T,j=1,2,…,m。
样品间常用的距离统计量有以下几种:
(1)布洛克距离(Block)。两项之间的距离就是每个变量值之差的绝对值之和。
![]()
(2)欧氏距离平方(Squared Euclidean Distance)。两项之间的距离是每个变量之差的平方和之平方根。
![]()
(3)切比雪夫距离(Chebychev)。两项之间的距离用最大的变量之差的绝对值表示。
![]()
当m个特征变量(指标)观测值的测量单位或数量级不同时,为提高分类效果,一般需要对数据进行预处理,常用的预处理方式有标准化和正规化。
类和类之间的距离有很多种定义法,常用的有以下几种:
第一种,类平均距离法。合并两类的结果使所有的两两项对之间的平均距离最小。项对的两个成员分别属于不同的类。
第二种,最短距离法。合并为一类后,类中的所有项之间的平均距离最小。两类间的距离就是合并后的类中所有可能的观测量对之间的距离平方。
第三种,最近邻法。首先合并最近的或最相似的两项,用两类间最近点间的距离代表两类间的距离。
第四种,最远邻法。用两类间最远点的距离代表两类间的距离。
第五种,重心聚类法。像计算所有各项均值之间的距离那样计算两类之间的距离,该距离随聚类的进行不断减小。
系统聚类法的基本思想是:先假定各个样品各自成一类,这时,各类间的距离就是各样品之间的距离,将距离最近的两类合并为一个新类;再计算新类与其他类间的距离,将距离最近的两类再合并,这样每次缩小一类,直到所有的样品都成为一类为止。然后根据需要或者根据给出的距离临界值确定分类数及最终要分的类。
2.基于系统聚类法的国际陆港空间布局聚类分析
有些城市综合指标好一些,一般适合建设国际陆港或者是建设规模较大的国际陆港;有些城市综合指标差些,一般建设规模较小的陆港。国际陆港布局层次聚类的目的就是对有可能建设国际陆港的城市进行分类,为国际陆港的宏观布局提供参考意见。
(1)聚类指标的选择。(https://www.xing528.com)
根据本章6.2的分析,影响国际陆港空间布局的因素主要有GDP、GDP增长率、进出口总额、进出口总额增长率、工业总产值、等级公路密度、批发零售业销售总额、货运量、交通区位和外商投资总额十个指标。
(2)聚类过程及结果。
1)由于指标量纲不一样,先对指标进行标准化。本书选择将指标在0~1间进行标准化。
2)聚类方法的选择。本书选择类平均距离法。对于等间隔测度的变量,本书采用欧氏距离平方。
3)聚类结果。本书将所有城市聚成四类,聚类结果如表6.2所示。
表6.2 系统聚类结果
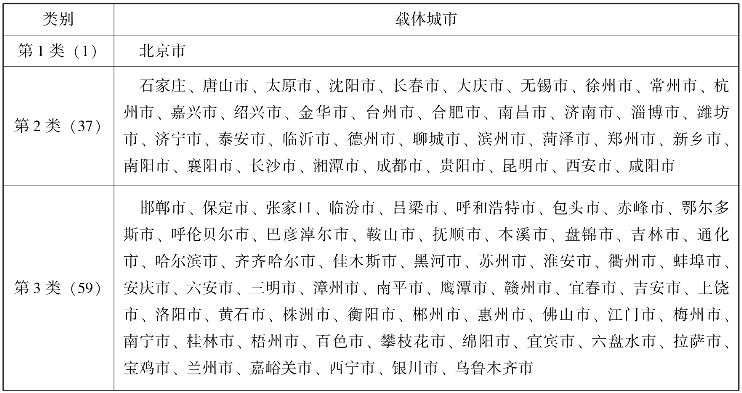
续表

3.聚类有效性评价
聚类过程可以看作一种无监督的学习过程,由于没有预先定义的分类或示例来表明数据集中在哪种期望的关系是有效的,因而多数聚类算法依靠专家经验进行。本书通过有效性评估模型(评价紧致度和分离),对聚类结果进行评价,从而确定最佳分类。
对于上述论域X={x1,x2,…,xn},每个样品xi有m个特征变量,原始数据矩阵如表6.3所示,其中![]() 称为总体样品的中心向量。
称为总体样品的中心向量。
表6.3 原始数据矩阵

设分类数为r,第j类的样品数为nj,第j类的样品记为:![]() 第j类的聚类中心为向量
第j类的聚类中心为向量![]() 其中
其中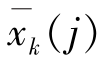 为第k个特征的平均值,即
为第k个特征的平均值,即
![]()
作F统计量:
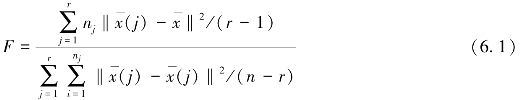
其中![]() 为
为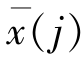 与
与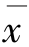 间的距离,
间的距离,![]() 为第j类中第i个样本
为第j类中第i个样本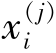 ()与其中心
()与其中心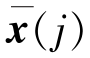 间的距离,称公式为F统计量,它遵从自由度为r-1,n-r的F分布,分子表示类与类之间的距离,分母表示类中样品间的距离。因此F越大,说明类与类间的距离越大,分类就越好。
间的距离,称公式为F统计量,它遵从自由度为r-1,n-r的F分布,分子表示类与类之间的距离,分母表示类中样品间的距离。因此F越大,说明类与类间的距离越大,分类就越好。
如果F>Fα(r-1,n-r)(α=0.05),则根据数理统计方差分析理论可知类与类间的差异是显著的,说明分类比较合理。
根据表6.2系统聚类的结果,运用式(6.1)计算其F统计量得:
F系统聚类=44.510 2
查F分布表得:
F0.05(4-1,147-4)=F0.05(3,143)=2.6
由于F系统聚类>F0.05(3,143),根据数理统计方差分析理论可知,运用系统聚类法将样本分为四类是比较合理的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




