在国际陆港中,单个企业的发展既受到其他相关企业的影响,也受到政府部门的影响。企业之间的影响既有竞争产生的抑制作用,也有互利产生的互补作用。而政府对企业的影响一般都是具有促进作用的,政府通过提供各种优惠政策促进企业的发展。本书构建了由物流企业和政府部门相互作用的国际陆港演化模型。
1.演化模型的构建
(1)假设。
假设1:在本书中,用yi表示国际陆港内物流企业i的服务产出,即假定运输、仓储、货代等物流企业i的服务所得是时间t的函数。
假设2:由于受到各种要素(包括原材料、土地、劳动力、市场规模等)和企业自身发展能力的影响和制约,各个物流企业的经济效益不可能无限增大,都有一个潜在的极限。设独立运作时,物流企业i存在着一个最大服务产出Ni,Ni是大于零的常数。
假设3:假定在国际陆港,物流企业i和物流企业j对对方的服务产出有一定的影响,影响系数为βij,如果物流企业i对物流企业j的服务产出有一定的促进作用,则βij>0;如果物流企业i对物流企业j的服务产出有一定的抑制作用,则βij<0。地方政府和海关等政府部门的集聚和提供的优惠政策也对物流企业的产出有一定的促进作用,政府部门z对物流企业i的产出影响系数为βzi,政府部门z对物流企业j的产出影响系数为βzj,则βzi>0,βzj>0。
假设4:假定物流企业的服务产出的增长率会随着产出水平的提高而下降,即物流企业的发展会对自身产出水平的增长产生阻滞作用。在本书中,定义自然市场规模饱和度为![]() 用
用![]() 反映物流企业i自身对产出增长的阻滞作用。
反映物流企业i自身对产出增长的阻滞作用。
假设5:物流企业i的产出的平均增长率为ri,ri一般为大于零的常数。
假设6:政府部门的产出L与政府自身的投入c和物流企业i的产出y成线性化关系,线性系数分别为k2和k1。
(2)物流企业产出的演化过程采用Logistic模型。
本书借用生物学的Logistic模型来描述国际陆港中运输、仓储、货代等物流企业的产出的增长变化的演化过程。物流企业i的经济效益方程为:
![]()
(3)政府部门z的产出采用线性化模型。政府部门的产出主要指政府部门获得的税收等各种财政收入。
![]()
(4)物流企业、政府等相互作用的模型。
本书以两个物流企业甲和乙、一个政府部门丙为例进行分析,则相互作用模型为:
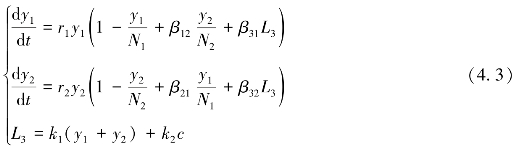
为了研究物流企业之间的演化趋势,即在t→∞的情况下,y1、y2的趋势,不用解方程组,只需对方程组平衡点进行稳定性分析。
对式(4.3)化简得:
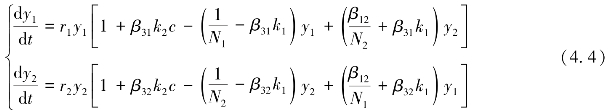
要求平衡点(稳定点),令式(4.4)为0,即:
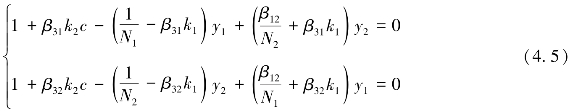
根据微分方程理论,当1-β31k1N1>0且1-β32k2N2>0时,可得方程组的四个平衡点,如表4.1所示。
表4.1 方程组平衡点

其中:
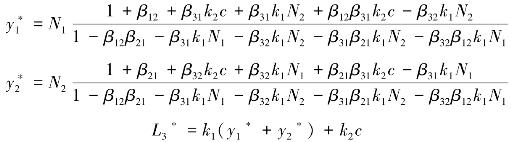
方程组的系数矩阵为:
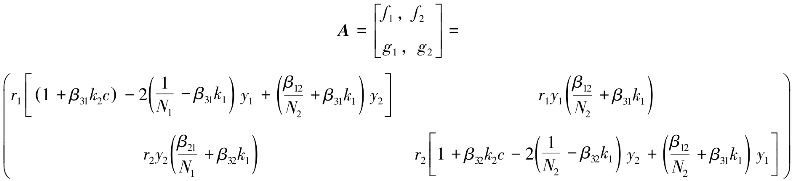
特征方程为:

将特征根记为λ1和λ2,解方程组(4.6)得:
![]()
根据常微分方程原理,可根据特征方程的系数![]() 或特征根λ1、λ2对平衡点的稳定性加以判断。
或特征根λ1、λ2对平衡点的稳定性加以判断。
2.模型稳定性分析
(1)β12>0,β21>0。
对于平衡点Q1:
系数矩阵A=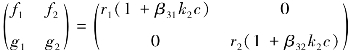
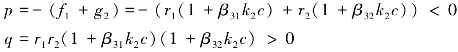
所以Q1不稳定。
对于平衡点Q2:
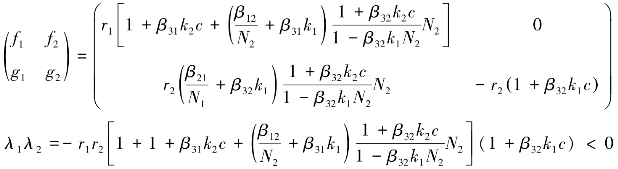
所以Q2不稳定。
对于平衡点Q3:
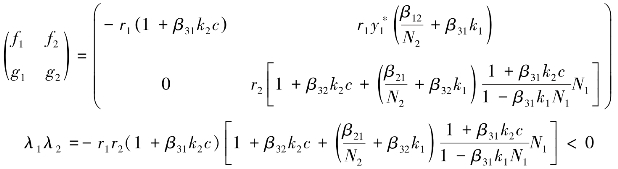
所以Q3不稳定。
对于平衡点Q4:
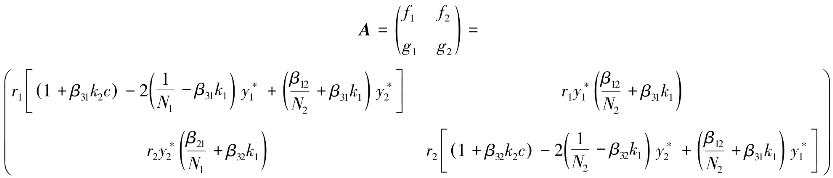
利用![]() 的方程可简化为:(https://www.xing528.com)
的方程可简化为:(https://www.xing528.com)
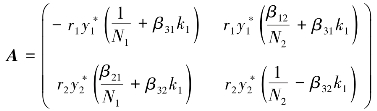
A的两特征值满足:
![]()
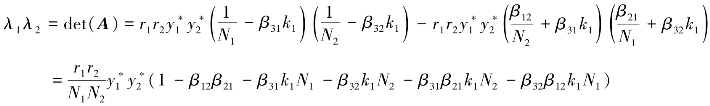
当λ1λ2>0时,Q4为稳定点。
所以平衡点Q4为稳定点的充分条件为:
![]()
由式(4.8)分析可得两点。
当β12β21<1。由于两企业具有对称性,则可得β12<1、β21<1,这表明甲乙企业对彼此具有一定的贡献,但贡献不大。即在这种情况下,国际陆港内提供物流服务的相关企业彼此的依赖度不是太大。
当β31β21k1N2<1,β32β12k1N1<1。由于N1、N2为较大的常数,因此,β31β21k1<1,β32β12k1<1。
在平衡状态下,物流企业甲的产出水平为:
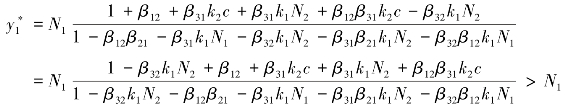
在平衡状态下,物流企业乙的产出水平为:
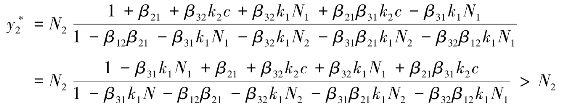
说明在平衡状态下,国际陆港内的物流企业的产出水平大于其在国际陆港外独立经营时的产出水平,且国际陆港内物流企业甲的产出水平系数为:
![]()
并随着β12、β31的增加而快速增加;物流企业乙的产出水平系数为:
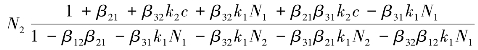
并随着β21、β32的增加而快速增加,即陆港内一个物流企业产出水平的增加将会使得其他物流企业产出水平成倍增加,政府的投入增加也将会使得物流企业的产出水平成倍增加。
由以上分析可知,国际陆港内物流企业的集聚能够增加物流企业自身的产出水平,这种集聚效应是国际陆港吸引企业入驻的根本原因。
(2)β12>0,β21<0。
对于平衡点Q1:
和上面分析一样,Q1不稳定。
对于平衡点Q2:
分析可得λ1λ2<0,则Q2不稳定。
对于平衡点Q3:
分析可得,当![]() 时,Q3稳定。
时,Q3稳定。
因此,当β12>0且![]() 时,Q3稳定。
时,Q3稳定。
(3)β12<0,β21>0。
对于平衡点Q1:
和上面分析一样,Q1不稳定。
对于平衡点Q2:
分析可得,当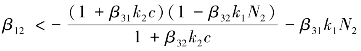 时,Q2稳定。
时,Q2稳定。
因此,当β21>0且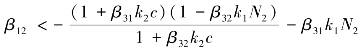 时,Q2稳定。
时,Q2稳定。
对于平衡点Q3:
分析可得λ1λ2<0,则Q3不稳定。
(4)β12<0,β21<0。
和前面分析类似,当:
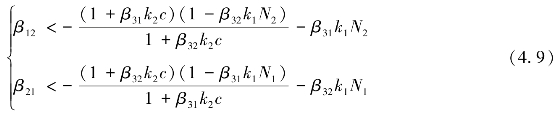
平衡点Q2、Q3均为稳定点。
当:
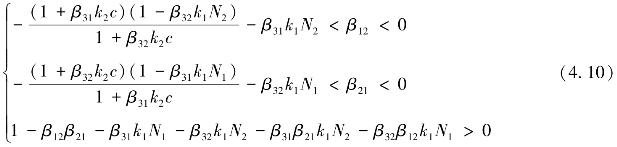
平衡点Q4为稳定点。
3.模型结果分析
(1)当国际陆港处于形成期时,国际陆港内的物流企业不多,彼此之间更多的是互利关系,这时候一般有β12>0,β21>0。这时候,当满足式(4.8)条件时,Q4为稳定点。由β12β21<1可知,在形成期,陆港内企业间的相互贡献不是很大,相互间依赖程度较小,且物流企业间能够共存。同时,由物流企业产出系数可知,政府的投入增加将会使物流企业的产出成倍增加,显然,政府在形成期的投入对企业的发展非常重要;由物流企业产出系数也知,陆港内一个物流企业产出水平的增加将会使其他物流企业产出水平成倍增加,显然,在形成期吸引企业加入陆港有利于陆港的发展。
(2)当国际陆港处于发展期时,国际陆港内的物流企业增多,竞争加剧,会出现β12>0、β21<0或者β12<0、β21>0的情况。以β12>0、β21<0为例进行分析,当β21<![]() 时,Q2稳定。说明物流企业乙对物流企业甲具有促进作用,而物流企业甲对物流企业乙有较大的抑制作用,长期下去,物流企业乙会最终破产或从陆港内迁出。因此,在国际陆港发展期,一些适应性强处于主导地位的物流企业会继续发展,而一些适应性差、处于不利地位的物流企业会破产或离开。
时,Q2稳定。说明物流企业乙对物流企业甲具有促进作用,而物流企业甲对物流企业乙有较大的抑制作用,长期下去,物流企业乙会最终破产或从陆港内迁出。因此,在国际陆港发展期,一些适应性强处于主导地位的物流企业会继续发展,而一些适应性差、处于不利地位的物流企业会破产或离开。
(3)当国际陆港处于成熟期时,国际陆港内物流企业数量趋于饱和,竞争非常激烈,会出现β12<0、β21<0的情况。当满足式(4.10)条件时,Q4为稳定点,说明物流企业间的抑制作用大于促进作用,只有在相互间的抑制作用不是很大的情况下,彼此才能共存。
(4)当满足式(4.9)条件时,Q2、Q3为局部稳定点。说明物流企业甲、乙间的抑制作用非常强,出现恶性竞争,彼此不能共存。最终结果是实力相对较强的物流企业生存下来,实力相对较弱的物流企业破产或迁出陆港,这时候,国际陆港步入衰退期。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




