在讨论反倾销裁决的问题中,可将决定实施反倾销用数字1表示,决议没有通过则用数字0表示。
x作为因变量出现在经济模型中,这种通过虚拟因变量取值讨论进行选择的回归模型称为离散选择模型。
现在约定因变量取值为0和1的二元选择模型中,下标i表示各不同的经济主体进行选择,因变量y i通过0和1的取值表示决策主体的具体选择结果,而影响决策主体选择自变量x i的取值。如果选择肯定yes的概率为p(y i=1/x i),则决策主体选择另一个选项no的概率为:
根据经典线性回归,我们可以构造线性概率模型:
根据线性概率回归模型可推导得知,根据统计数据得到的回归结果不一定能够保证回归模型的因变量虚拟拟合值介于[0,1]区间内。为避免出现回归模型的因变量预测值偏离0或1的情形,需要限制因变量的取值范围并对回归模型式进行必要的修正。离散选择模型根据极大似然估计估计出回归方程,预测事件出现的概率。
在讨论国际贸易委员会是否通过对华反倾销裁决的问题中,用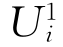 表示第i个人选择通过的效用
表示第i个人选择通过的效用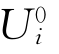 表示第i个人选择反对的效用,其效用均为随机变量。
表示第i个人选择反对的效用,其效用均为随机变量。
将(1)-(2),得:
记:
则有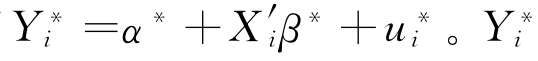 为过渡变量(潜在的),这个变量是不可观测的。
为过渡变量(潜在的),这个变量是不可观测的。
当效用差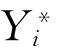 大于零,则应该选“1”,即赞同反倾销法案;
大于零,则应该选“1”,即赞同反倾销法案;
当效用差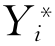 小于零,则应该选“0”,即反对反倾销法案。(https://www.xing528.com)
小于零,则应该选“0”,即反对反倾销法案。(https://www.xing528.com)
则
通过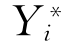 将自变量与事件发生的概率联系起来,为概率提供了一个潜在的结构模型。
将自变量与事件发生的概率联系起来,为概率提供了一个潜在的结构模型。
现在的问题是F(·)服从何种分布,采用累积标准正态概率分布函数的模型称作Probit模型,或概率单位模型,用正态分布的累积概率作为Probit模型的预测概率。采用logistic函数的模型称作logit模型,或对数单位模型。本节采用Logit模型。
因为:
如果我们取F(·)为逻辑函数(LOGIT),即: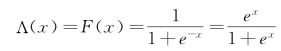
(满足分布函数的条件)
于是有:
为了简化模型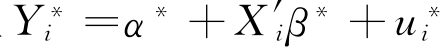 ,令
,令
则有:
则回归模型为ln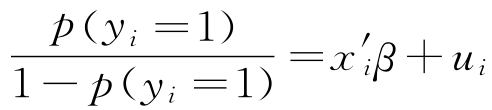
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




