投资组合的风险与收益探析

投资组合理论认为，若干种证券组成的投资组合，其收益是这些证券收益的加权平均数，但是其风险不是这些证券风险的加权平均数，这是因为投资组合能降低风险。这里的“证券”是“资产”的代名词，它可以是任何产生现金流的东西，如一项生产性实物资产、一条生产线或者是一个企业。

（一）投资组合的预期收益率

两种或两种以上证券的组合，其预期收益率可以直接表示为

式中，Ki是第i种证券的预期收益率；Wi是第i种证券在全部投资额中的比重；n是组合中的证券种类总数。

【例2-27】某投资公司的一项投资组合中包含A，B和C三种股票，权重分别为30%，40%和30%。三种股票的预期收益率分别为15%，12%和10%。求该投资组合的预期收益率。

解：该投资组合的预期收益率=30%×15%+40%×12%+30%×10%

=12.3%

（二）投资组合的风险

投资组合的整体风险，可以用投资组合预期收益率的标准差来表示，但投资组合预期收益率的标准差并不是单个证券标准差的简单加权平均。投资组合的风险不仅取决于组合内的各证券的风险，还取决于各个证券之间的关系。

1.两种证券组合的整体风险

两种证券组合的收益率的方差：

式中，r12为相关系数，反映两种证券收益率的相关程度，即两种证券收益率之间相对运动的状态，理论上，相关系数介于区间[-1，1]内。

在实际中，两项证券的收益率具有完全正相关和完全负相关的情况几乎是不可能的。绝大多数证券两两之间都具有不完全的相关关系，即-1＜r12＜1。因此，证券投资组合可以降低风险，但不能完全消除风险。组合中的证券种类越多，风险越小。若投资组合中包括全部证券，证券组合就不承担非系统风险，只承担系统风险。因此，只要两种证券之间的相关系数小于1，证券组合收益率的标准差就小于各证券收益率标准差的加权平均数。(www.xing528.com)

2.多种证券组合的整体风险

一般来讲，随着证券组合中证券个数的增加，证券组合的风险会逐渐降低。当证券的个数增加到一定程度时，证券组合的风险程度将趋于平稳，这时组合风险的降低将非常缓慢直到不再降低，如图2-9所示。

图2-9　投资组合的风险

值得注意的是，在风险分散的过程中，不应当过分夸大证券多样性和证券个数的作用。实际上，在证券组合中证券数目较少时，增加证券的个数，分散风险的效应会比较明显，但证券数目增加到一定程度时，风险分散的效应就会逐渐减弱。经验数据表明，组合中不同行业的证券个数达到20个时绝大多数非系统风险均已被消除掉。此时，如果继续增加证券数目，对分散风险已经没有多大的实际意义，只能增加管理成本。另外不要指望通过证券多样化达到完全消除风险的目的，因为系统风险是不能够通过风险的分散来消除的。

（三）投资组合的非系统风险（β系数）

投资组合的βp等于被组合各证券β值的加权平均数：

如果一个高β值股票（β＞1）被加入一个平均风险组合（βp）中，则组合风险将会提高；反之，如果一个低β值股票（β＜1）加入一个平均风险组合中，则组合风险将会降低。所以，一种股票的β值可以度量该股票对整个组合风险的贡献，β值可以作为这一股票风险程度的一个大致度量。

【例2-28】某证券组合中有三种股票，有关的信息如表2-2所示，计算证券组合的β系数。

表2-2　某证券组合的相关信息

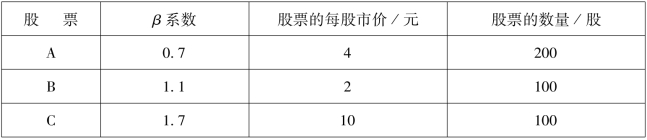
解：首先计算A，B，C三种股票所占的价值比例：A股票的价值比例：（4×200）/（4×200+2×100+10×100）=40%

B股票的价值比例：（2×100）/（4×200+2×100+10×100）=10%

C股票的价值比例：（10×100）/（4×200+2×100+10×100）=50%然后，计算加权平均β系数，即为该证券组合的β系数：

βp=40%×0.7+10%×1.1+50%×1.7=1.24